RetinaNet论文总结（Focal Loss）

写在前面
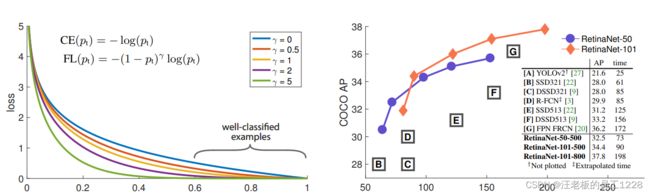
RetinaNet在2017年提出，是一个里程碑性质的模型。在目标检测领域，作为一个one-stage网络，它首次超过了当时流行的two-stage模型。RetinaNet在模型方面没有颠覆性的创新，使之超越当时流行目标检测模型的原因是提出了新颖的loss计算方式：Focal Loss
参考文章和视频在这里！
本文部分图片来源于上行的参考视频

---

---

一、RetinaNet结构

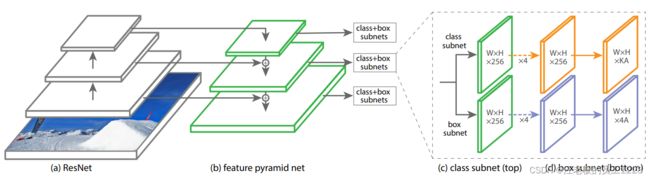
RetinaNet结构总的来说是“backbone+2*subnets”。 其中backbone内还采用了FPN结构，anchors在不同金字塔层的feature map上生成。2个subnets分别实现cls和box的预测任务。

1. Backbone

（1）预训练ResNet + FPN

文中使用了两种ResNet模型：ResNet-50和ResNet-101。皆在ImageNet1K数据集上预训练。

FPN网络基本与原论文一致, 参考pytorch代码，不同点在于：1. 这里未使用C2生成P2。2. P6从P5基础上生成，而不是C5。3. 使用在P6基础上下采样的P7以应对较大size的目标的检测。 之后的两个subnets使用的是P3~P7这5层feature map作为输入。

（2）Anchors

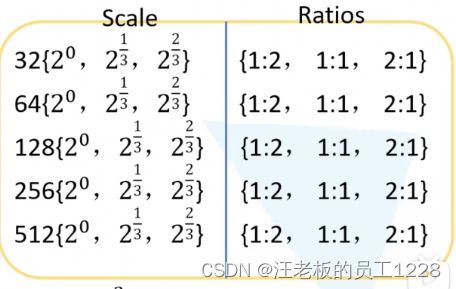
针对backbone网络输出的P3~P7这5个level的feature map，论文设置了不同尺度，不同长宽比例的anchors。

• Scale
  作者先设置了 anchors的base尺寸 。从P3~P7，由于感受野的增大，feature map的size减小，越来越适合更大size目标的检测。于是P3~P7上生成anchors的base尺寸大小也逐渐增加，如上图所示，即P3 -> 32; P4 -> 64; ······以此类推。注意，这里的base尺寸指的是anchors在原图上的大小，并且是单边（也就是说anchors面积是base尺寸的平方）。

  作者还设置了 缩放因子。即每个base尺寸皆有 $(2^0,2^{1/3},2^{2/3})$ 这三个尺寸的缩放，分别与base尺寸相乘得到anchor的真实面积平方根。

• Ratios
  anchors长宽比例设置为三种：{1:2, 1:1, 2:1}。

所以，每个feature map的像素上都会生成3 x 3 = 9个anchors。

2. Subnets——预测cls与box的分支

Subnets的两个子网分支是并行的，是结构相似的全卷积网络，它们共享FPN的feature map。

两个subnets在除了在最后一个卷积层参数不一样以外，前4个卷积层设置完全一样：皆为3x3大小，步长为1，channels为256的卷积+ReLU激活函数。 input image的size并未改变，channels变为256。

• 对于cls分支，最后一个卷积层后不接激活函数，卷积核为3x3大小，步长为1，channels为K*A大小。其中K为数据集的总类别数，A为每个level的anchors数量，
  代表每个anchors的预测类别（用one-hot编码形式表示）。

• 对于box分支，最后一个卷积层后不接激活函数，卷积核大小和步长与cls分支一样，只是channels为4*A大小，A为每个level的anchors数量，
  代表每个anchors的四个参数x, y, w, h ，皆为对应GT的offset形式。

即对于每个level的backbone输出，feature map的每一个像素点上都会生成A = 9个anchors，anchors的尺寸和比例在“一、1.(2)”中已介绍，subnets则会预测所有anchors的信息。

3. 模型总损失函数

（1）Anchors的分配

论文在RPN分配anchors的基础上做了改动，下表为本论文中anchors的分配标准。

IOU with GT-box	分配情况
[0.5, 1]	正样本
[0.4, 0.5)	丢弃
[0, 0.4)	负样本

（2）总损失函数的计算

总Loss由两部分loss组成，分别来自两个subnets。

具体的计算方式上图写的很直观，联系anchors的分配表便可以理解了。图源参考视频。

---

二、A novel loss: Focal Loss

接下来便是本论文的重榜，一种直接让one-stage模型如虎添翼赶英超美的全新样本loss计算方式：Focal Loss。

作者在论文里猜想并验证了导致以前的one-stage模型落后的原因是class imbalance（类别不平衡）问题。 具体来说就是，训练阶段，检测器在每张输入图片上会产生非常多的候选区域，但是只有其中一小部分包含了目标，大部分都为background，也就是负样本远多于正样本。这会导致两个问题：1）负样本区域虽易检测，但是对模型学习无较大贡献；2）过量的易检测的负样本会压倒训练，导致模型学习效果差。

由于负样本区域大部分属于易检测的目标，作者由此发散讨论了难分/易分样本对于模型训练的影响。作者认为hard example（难分样本）对于模型学习是更有效的，而easy example（易分样本）则对模型的学习贡献不大。联系上段，easy example太多甚至会影响模型正常的学习。这也是可以感性理解的，也就是易分样本的loss压过了难分的样本，真正对模型学习有效的loss反而被忽略。于是作者提出Focal Loss，重点关注hard example的loss对总loss的贡献。

值得注意的是，class imbalance问题其实在two-stage模型里也存在，只是two-stage模型通过正负样本比例调整、RPN输出候选区域后通过前景分数过滤大部分easy negative（易分负样本），减缓了此问题，使的此问题对two-stage模型的影响不是那么大。但是在one-stage模型里，这确是致命的。

1. Balanced Cross Entropy

论文先循序渐进，对最基本的Cross Entropy进行平衡改进，引入${\alpha }_t$平衡因子调整单个正负样本损失的权重，也就是针对正负样本loss加权处理后，再计算总loss。Balance后的单个样本的CE损失如下所示：
$$BalancedCE(p_t)=-{\alpha }_{t}log(p_t)$$
其中$p_t$、${\alpha }_t$针对单个样本，计算方式如下。y是此样本的GT值，为1代表是正样本（前景）；$p$是此样本为正样本的概率。
$$p_t=\{\begin{array}{rc}p,& ify=1\\ 1-p,& otherwise\end{array}$$

$${\alpha }_t=\{\begin{array}{rc}\alpha ,& ify=1\\ 1-\alpha ,& otherwise\end{array}$$

2. Focal Loss

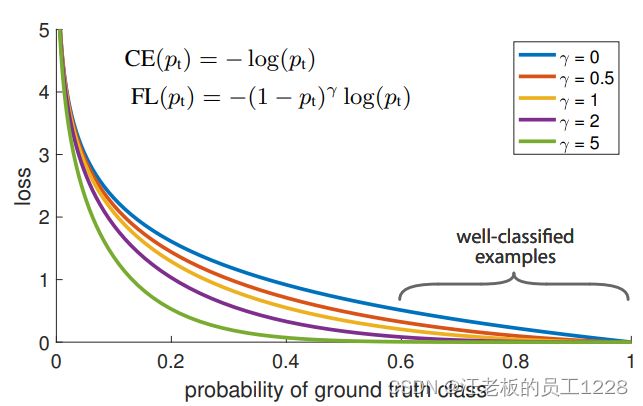
上图中蓝色曲线对应普通Cross Entropy损失函数随$p_t$变化情况。$p_t$越大代表此样本越易分（easy example）。 观察此损失函数的曲线，并未很好拉开易分样本和难分样本之间的loss差距。于是乎作者由“改变易/难分样本loss之间倍数”的想法出发，在CE基础上引入$\gamma$聚焦因子，提出了Focal Loss损失函数：

$$FL(p_t)=-(1-p_t{)}^{\gamma }log(p_t)$$

上图中作者绘制出了几个$\gamma$取值时FL曲线变化情况。可以看到，FL曲线确实“改变了易/难分样本loss之间倍数”，让易分样本的loss降低的比难分样本多得多。相当于让总loss中难分样本的loss占比更大，loss更关注这一块对模型有用的loss。

作者还尝试了在FL的基础上也加入${\alpha }_t$平衡因子得到改进后的FL，公式如下。论文中证实改进的FL相较基础版FL对模型最后效果有小小的提升。

$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }log(p_t)$$

其中$\alpha ;\gamma$都是超参数。