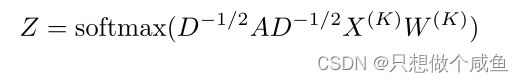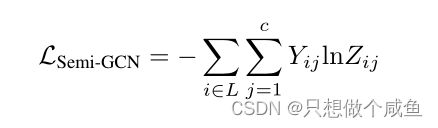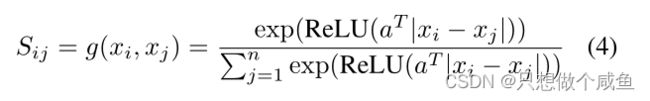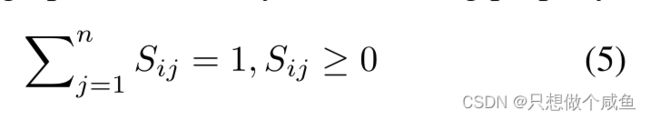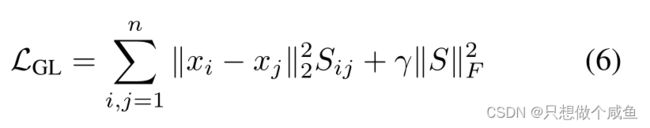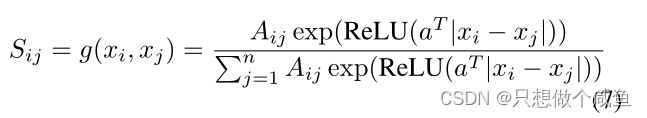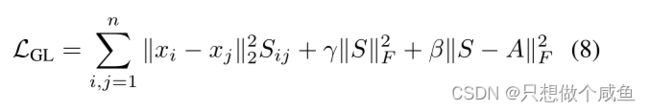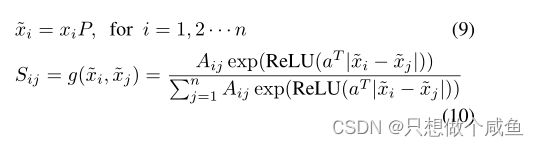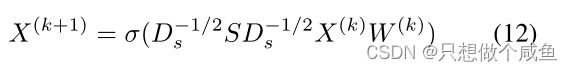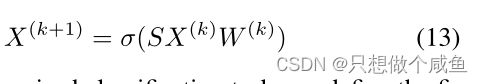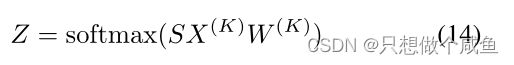GLCN:Semi-supervised Learning with Graph Learning-Convolutional Networks

1、前言

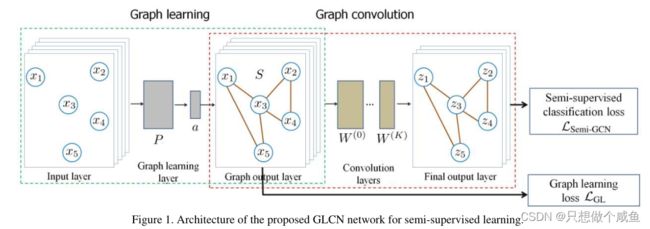
.现有的图CNN通常使用对于半监督学习任务可能不是最优的固定图。在本文中，提出了一种新的用于图数据表示和半监督学习的图学习卷积网络（GLCN）。GLCN的目标是通过将图学习和图卷积两者集成在统一的网络架构中，学习最适合于半监督学习的图CNN的最优图结构。

GLCN的主要思想是通过在统一的网络架构中同时集成图学习和图卷积来学习最适合于半监督学习的图CNN的最优图表示。

2、相关工作

回顾之前提出的基于GCN的半监督学习

设,表示P维的n个向量集合。

也可以理解为我们刚开始的初始嵌入。

设,其中X表示节点结合，A表示对应节点之间的关系，

A可以理解为边的关系，邻接矩阵

给定输入X和图A，GCN 在隐藏层中进行以下分层传播：

 这是经典的卷积过程了，是激活函数，例如ReLU；D是度矩阵，A是输入的邻接矩阵，与度矩阵进行操作时归一化邻接矩阵（不会出现较大或者古怪的值），emmm，x是输入的节点特征，W是权重矩阵

 这是分类时会用到的，归一化为0~1之间的数，以便更好地做出预测对于输出结果进行多分类，确定属于哪个类别

 这个是交叉熵损失函数，将每一个标签Zij和真实标签Yij进行比较，求出损失进行最优化。

3、图学习模块

（1）仅基于数据特征建立邻域结构

给定一个输入，目标是寻求一个非负函数,表示数据和之间的成对关系，由权重向量参数化,学习图S为：

 其中ReLU（·）=max（0，·）是一个激活函数，它保证Sij的非负性。在S的每一行上的上述softmax操作的作用是保证学习图S能够满足以下性质：

 我们通过最小化以下损失函数来优化最优权重向量a，

 如果Xi-Xj的值越大，那么我们就调整Sij的值越小，已达到整个损失值最小的目的。反之，如果Xi-Xj的值越小，那证明当前的Sij正常不用管。第二部分，是为了控制矩阵S的稀疏性。

补：

由于L1范数的天然性质，对L1优化的解是一个稀疏解，因此L1范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏，去掉一些没有信息的特征，例如在对用户的电影爱好做分类的时候，用户有100个特征，可能只有十几个特征是对分类有用的，大部分特征如身高体重等可能都是无用的，利用L1范数就可以过滤掉。

使用了低秩和稀疏约束，数据的全局子空间和局部几何结构都被重构系数矩阵捕获，同时强制数据的低维嵌入以遵循低秩和稀疏性。这样，重构系数矩阵学习和SL联合进行，可以保证整体最优。此外，采用稀疏矩阵对噪声进行建模，这使得对不同类型的噪声具有鲁棒性。

• 稀疏表示

用字典中部分元素的 线性组合去表示样本。

• 低秩表示

秩度量相关性。低秩说明包含大量的冗余信息。利用这种冗余信息，可以对缺失数据进行恢复，也可以对数据进行特征提取。

（2）将先前的初始图A与X合并来自动建立数据的邻域结构

当初始图形A可用时，我们可以将其作为：

 还可以通过考虑学习损失函数中的正则化项，将A的信息合并为

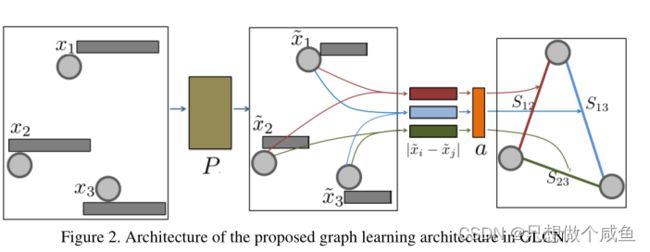
当输入数据X的维数p较大时，由于需要训练较长的权重向量a，上述g（xi，xj）的计算可能效率较低。此外，欧几里得距离的计算∥xi− X轴∥对于大维p，损失函数LGL中数据对之间是复杂的。为了解决这个问题，建议在低维子空间中进行图学习。通过由投影矩阵P参数化的单层低维嵌入网络来实现这一点P∈ Rp×d，d

其中A表示初始图。如果它不可用，我们可以在上面的更新规则中设置Aij=1。损失函数变为

 总结：GL架构确实提供了一种非线性函数来预测/计算节点对之间的邻域概率。GLCN的目标是学习GCN网络的最优图表示，并同时集成图学习和卷积以提高它们各自的性能。

4、图卷积模块

图学习层旨在为图卷积层提供最佳自适应图表示S。也就是说，在卷积层中，它基于图学习层返回的自适应邻居图S执行逐层传播规则，即：

 其中S就是学习到的图
又因为有了公式5的性质，那么说就不需要再对图进行标准化，所以公式12变成了：

 于半监督分类任务，我们将最终感知器层定义为：

 通过最小化以下损失函数来联合训练整个网络参数

 5、核心代码部分

（1）图学习模块

class SparseGraphLearn(object):
    """Sparse Graph learning layer."""
    def __init__(self, input_dim, output_dim, edge, placeholders, dropout=0.,
                 sparse_inputs=False, act=tf.nn.relu, bias=False, **kwargs):
        allowed_kwargs = {'name', 'logging'}
        for kwarg in kwargs.keys():
            assert kwarg in allowed_kwargs, 'Invalid keyword argument: ' + kwarg
        name = kwargs.get('name')
        if not name:
            layer = self.__class__.__name__.lower()
            name = layer + '_' + str(get_layer_uid(layer))
        self.name = name
        self.vars = {}

        if dropout:
            self.dropout = placeholders['dropout']
        else:
            self.dropout = 0.

        self.act = act
        self.num_nodes = placeholders['num_nodes']
        self.sparse_inputs = sparse_inputs
        self.bias = bias
        self.edge = edge

        # helper variable for sparse dropout
        self.num_features_nonzero = placeholders['num_features_nonzero']

        with tf.variable_scope(self.name + '_vars'):
            self.vars['weights'] = glorot([input_dim, output_dim], name='weights')#1433*70
            self.vars['a'] = glorot([output_dim, 1], name='a')#70*1
            if self.bias:
                self.vars['bias'] = zeros([output_dim], name='bias')

    def __call__(self, inputs):
        x = inputs#2780*1433
        # dropout
        if self.sparse_inputs:
            x = sparse_dropout(x, 1-self.dropout, self.num_features_nonzero)
        else:
            x = tf.nn.dropout(x, 1-self.dropout)

        # graph learning
        h = dot(x, self.vars['weights'], sparse=self.sparse_inputs)# 2780*70   特征变换
        N = self.num_nodes
        edge_v = tf.abs(tf.gather(h,self.edge[0]) - tf.gather(h,self.edge[1]))#13264*70
        edge_v = tf.squeeze(self.act(dot(edge_v, self.vars['a'])))#13264
        sgraph = tf.SparseTensor(indices=tf.transpose(self.edge), values=edge_v, dense_shape=[N, N])
        sgraph = tf.sparse_softmax(sgraph)
        return h, sgraph

（2）损失函数部分

    def _loss(self):
        # Weight decay loss
        for var in self.layers0.vars.values():
            self.loss1 += FLAGS.weight_decay * tf.nn.l2_loss(var)
        for var in self.layers1.vars.values():
            self.loss2 += FLAGS.weight_decay * tf.nn.l2_loss(var)

        # Graph Learning loss
        D = tf.matrix_diag(tf.ones(self.placeholders['num_nodes']))*-1
        D = tf.sparse_add(D, self.S)*-1
        D = tf.matmul(tf.transpose(self.x), D)#70*2708
        self.loss1 += tf.trace(tf.matmul(D, self.x)) * FLAGS.losslr1
        self.loss1 -= tf.trace(tf.sparse_tensor_dense_matmul(tf.sparse_transpose(self.S), tf.sparse_tensor_to_dense(self.S))) * FLAGS.losslr2

        # Cross entropy error
        self.loss2 += masked_softmax_cross_entropy(self.outputs, self.placeholders['labels'],
                                                  self.placeholders['labels_mask'])
       
        self.loss = self.loss1 + self.loss2

6、实验

（1）收敛性

可以注意到，GLCN在收敛时获得的交叉熵值明显低于GCN，这清楚地证明了GLCN模型的较高预测精度。此外，GLCN的收敛速度略慢于GCN，这表明GLCN具有效率

 （2）分辨力

图4分别展示了GCN[11]和GLCN的第一卷积层输出的特征图的2D t-SNE可视化。不同的类用不同的颜色标记。可以注意到，不同类别的数据在我们的GLCN表示中分布得更清晰、更紧凑，这证明了GLCN在执行图节点表示和半监督分类任务时所需的辨别能力。

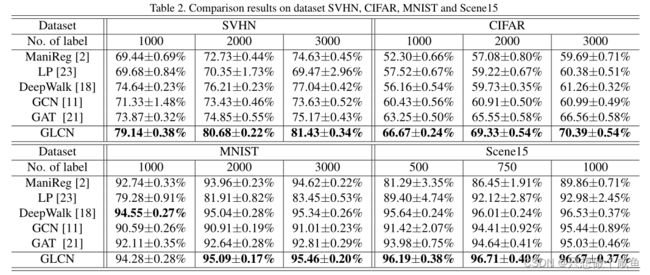
 （3）整体实验结果