【论文分享】Learning Graphs for Knowledge Transfer with Limited Labels

【CVPR2021】有限标签知识转移的学习图

---

---

以下是全文翻译，如有问题，请批评指正。

摘要

       固定输入图是利用图卷积网络 (GCN) 进行知识转移的方法的支柱。标准范式是利用输入图中的关系，使用 GCN 将信息从图中的训练节点转移到测试节点；例如，半监督、零样本和少样本学习设置。我们提出了一个通用框架，用于学习和改进输入图，作为基于 GCN 的标准学习设置的一部分。此外，我们通过在中间层输出上应用三元组损失，为图中的每个节点使用相似和不同邻居之间的额外约束。我们在 Citeseer、Cora 和 Pubmed 基准数据集上展示了半监督学习的结果，以及在 UCF101 和 HMDB51 数据集上的零/少拍动作识别结果，显着优于当前方法。我们还提供了定性结果，可视化我们的方法学习更新的图连接。

1 介绍

       基于图卷积网络 (GCN) 的技术已广泛用于标记数据有限的任务的迁移学习，例如，半监督学习 [24, 55] 和零样本/少样本学习 [57, 9, 12]来自测试类的零个或几个样本。这些方法依赖于捕获图中节点之间关系的输入图。给定这个输入图，然后使用 GCN 在图的节点之间传播和同化信息，遵守图连接中表达的关系。该框架的目标是将信息从训练节点传输到测试节点。这是一个相当通用的框架，适用于各种任务，具有不同的节点表示和输入图。例如，对于半监督学习[24, 55]，知识从训练样本转移到测试样本；节点代表数据集中的每个样本数据点，输入图代表这些样本之间的关系。零样本学习 [57, 9, 12] 将知识从训练类转移到测试类；节点表示类的语义嵌入（例如 word2vec [34]、sentence2vec [40]），输入图可以来自各种来源（例如 Word Net [35]、NELL [2]、NEIL [ 6]）。小样本学习在基于类或样本的节点之间转移知识 [12, 23]。
       迄今为止讨论的这些基于 GCN 的技术的主要限制之一是，由邻接矩阵捕获的输入图结构是固定的。 根据设计，基于 GCN 的方法严重依赖于输入图，而嘈杂或低质量的图对性能有很大的影响。 在这项工作中，我们结合 GCN 训练的其余部分，探索了输入邻接矩阵随时间的自适应学习； 即，用于训练底层任务（例如，半监督学习或零/小样本学习）的损失也用于更新输入邻接矩阵的结构。 我们凭经验表明，我们的学习图为下游任务产生了更好的结果。我们提出的方法是一种直接的算法，通过学习更好的节点表示并使用这些来重新计算邻接矩阵来更新图的结构。 请注意，我们没有添加任何新的网络权重来学习。 这与其他相关的图学习工作 [21, 10] 形成鲜明对比，后者具有单独的专用网络和特殊的损失函数来更新邻接矩阵。 由于通过 GCN 学习的节点表示可以捕获与下游任务更好的相关性，因此生成的图往往比来自外部源的输入图更好。 图 1 展示了一个这样的更新，我们从中学习到了“搅拌面糊”类的更好的连接。 基于语言的知识图 (KG) 将“batter”与动词“batting”（显示为“input”）相关联，我们的方法纠正了这个错误，并产生了更有意义的联系。

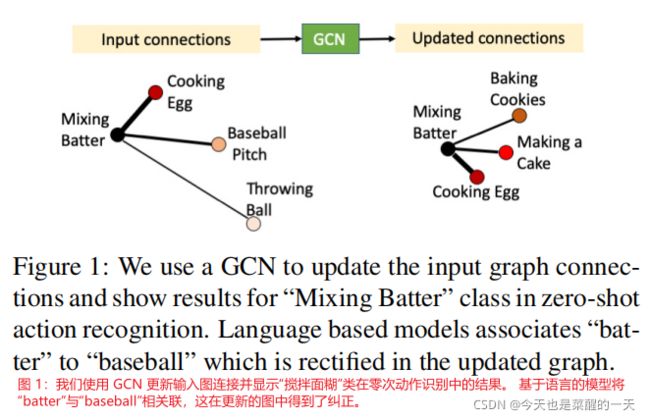
       实施上述直截了当的方法有两个关键问题。首先，在没有任何其他约束的情况下，更新一个密集或完全连接的图往往会为结构提供任意更新，甚至最终导致退化解决方案（例如，所有边的权重相同）。其次，如果图连接是稀疏的（通常是这种情况），则没有机制可以学习在学习过的图中添加或删除连接。简单的启发式方法，例如每个节点的固定度数可以是一个解决方案，但它们往往是次优的，因为不同的节点可能具有不同数量的应该连接到的相关节点。此外，每个下游任务可以对节点的度数有特定领域的约束；例如，对于零镜头动作识别，[12] 观察到全连接图对性能有害，并凭经验确定合适的程度。为了解决上面讨论的两个缺点，在遵守特定领域的约束的同时，我们建议在中间输出节点上使用三元组损失公式——即在我们的图学习步骤之后但在图被传递给下游任务的 GCN 框架之前的节点特征。我们的公式为每个节点选择正邻居和负邻居，并使用它们对其程度添加约束。通过确保负邻居比正邻居更远，可以避免退化的解决方案。因此，图学习步骤使用下游任务损失和三元组损失进行训练。
       总之，我们的贡献是一种能够更新基于GCN的迁移学习框架输入图和一个避免退化解决方案并且允许度数约束灵活性的三元组损失公式的简单学习方法。我们证明了我们的方法在半监督、零样本和少样本学习设置上的有效性。 对于半监督学习，我们使用基于引文网络数据集（如 Cora、Citeseer 和 Pubmed）构建的附带有明确定义的输入图的通用框架[24]。对于零样本/少样本学习，我们专注于输入 KG 由句子转换成向量[40] 嵌入构建的动作识别管道 [12]。

2 相关工作

2.1 图网络

       图网络已被用于大量应用，如场景理解 [59, 62]、分割 [54]、动作识别 [13, 60] 等。关于图神经网络和图卷积网络的多项工作包括 [11, 47、23、8、17、24、48、64]。 光谱图理论是由Hammond 等人引入的，最近关于谱图理论的工作包括 Defferrard 等人以及 Kipf 和 Welling [24]。过去十年中图网络中的其他一些工作包括 [20, 32, 67]。
       半监督学习。 一些作品 [18, 24, 25, 30, 43, 55] 利用 GCN 框架进行半监督学习。 此类作品通常使用引文网络数据集，如 Citeseer、Cora 和 PubMed [49, 39]，以及蛋白质相互作用数据集 [70] 用于半监督学习的实验。 我们的方法利用 Kipf 和 Welling [24] 提出的 GCN 框架作为我们的 GCN 算子并且用引文网络数据集作为我们的输入。
       图学习网络。 与我们的研究最相关的是最近关于半监督学习的图学习网络的工作 [10, 21]，它提出了一种新的损失函数来学习图中的边权重。我们不是使用单独的网络来输出边权重，而是从原始 GCN 公式中获取中间输出并直接更新邻接矩阵。我们的技术更加灵活，允许在必要时更新节点特征和边权重以及连接。与 Jiang 等人的研究不同，我们的方法对输入节点特征维度长度增加引起的复杂性问题也具有鲁棒性。 [21]。Chen使用启发式更新图拓扑以防止 GNN 中的过度平滑。Kim应用图神经网络模型来学习输入图中的边权重以进行小样本学习，根据与其他标记节点的连接性预测标签。相比之下，我们基于 GCN 框架进行零/少量学习，其中图中的节点代表类而不是单个样本。

2.2 零/小样本学习

       零/少镜头图像分类领域的广泛研究包括 [4, 16, 26, 29, 37, 44, 45, 46, 50, 53, 56, 66] 的作品。 这些零样本技术之一 [57] 在输入 KGs 上使用 GCN 将知识边缘从可见类转移到不可见类。 在此框架的基础上，[12] 提出了基于 3 个不同 KGs 的框架，用于零/少镜头动作识别。 由于其灵活性、使用不同的输入图和两个下游应用程序，我们使用 [12] 的管道作为我们的 GCN 框架，用于零/小样本学习实验。 零/少镜头动作识别领域的其他研究包括 [1, 9, 14, 19, 28, 33, 36, 61, 68, 69]，其中 [9] 还使用了一个基于 GCN 的系统构建在 ConceptNet 上 [52]。 我们将证明我们的方法优于该领域中最先进的方法。

3 GCN-框架概述

       用于半监督学习的 GCN 网络是基于光谱 GCN 形式的两层网络，由 [24] 引入并在等式 1 中给出。
$$\begin{array}{r}{H}^{l+1}=g(H^l,A)=\sigma (D^{-1/2}A{D}^{-1/2}{H}^l{W}^l)\end{array}\text{\hspace{1em}(1)}$$
       在这个等式中，$g$ 是 GCN 操作，它将第 $l$ 层的输出 $H^l$ 和具有自连接的邻接矩阵 $A$ 作为输入。 这里，$D$是$A$的节点度矩阵，$W^l$ 是第 $l$ 层的权重矩阵，$\sigma$ 分别是激活函数（例如 ReLU）。 $D^{-1/2}A{D}^{-1/2}$ 操作从现在开始称为邻接矩阵的归一化。 我们使用 [57] 提出的 GCN 框架进行零样本学习。 算法 1（黑线）中提供了高级概述，补充中提供了更多详细信息。

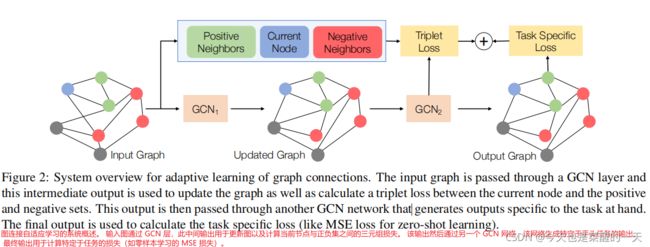
4 方法

       从训练节点到测试节点的知识转移在很大程度上依赖于输入图的质量。 更好地放置样本/类之间的相互关系会导致基于 GCN 的迁移学习框架的更好输出。 在没有随附的标记图（存在于引文数据集中）的情况下，一些研究探索了不同类型的 KG（例如，[9, 12]）。 所有基于 GCN 的框架，除了半监督学习和零/小样本学习的少数例外，在整个 GCN 网络中使用固定的邻接矩阵。 然而，如前所述，能够学习邻接矩阵既可取又具有挑战性。 我们首先讨论自适应更新邻接矩阵的算法，然后介绍我们如何训练这个公式。

4.1 自适应更新邻接矩阵

       令 GCN1 成为提供中间输出的原始网络的一部分，而原始 GCN 的其余部分是 GCN2。 GCN1 的输出用于重新计算邻接矩阵，其中边权重是 GCN1 输出节点值的余弦相似度。 然后，我们使用新的邻接矩阵作为 GCN2 的输入，从下一个 epoch 开始。
       更正式地，$h_k^{l-1}$ 是第 $(l-1)$ 层第 $k$ 个节点的输出。 这通过权重为 $W^l$ 的第 $l$ 个卷积层。 然后，对于每个节点，都有一个基于其邻接 $N_i$ 的加权聚合，其中边权重由连接节点 $i$ 和 $k$ 的 $c_{ik}$ 表示。 因此，GCN1 中第 $i$ 个节点的第 $l$ 层输出 $h_i^l$ 由等式 2 给出，其中 $\sigma$ 是非线性（例如 ReLU）。
$$\begin{array}{r}{h}_i^l=\sigma (\sum _{kϵN_i}{c}_{ik}{h}_k^{l-1}{W}^l)\end{array}\text{\hspace{1em}(2)}$$
       同理，hlj是第l层第j个节点的输出。 然后，连接节点si和j的新边权重由hli和hlj的余弦相似度给出，如等式3所示。
$$\begin{array}{r}{c}_{ij}=Normalize\left(\frac{h_i^l\cdot h_j^l}{||h_i^l||||h_j^l||}\right)\end{array}\text{\hspace{1em}(3)}$$
       这里 Normalize 是 [24] 使用的邻接矩阵归一化。 我们用 Ain 表示原始邻接矩阵，用 Aupdated 表示更新的邻接矩阵。 GCN1 在 Ain 上运行，而 GCN2 在 Aupdated 上运行。 如果我们不保持这个约束，对邻接矩阵的不正确更新将导致下一次更新期间图变得更糟，从而导致多米诺骨牌效应。 为了帮助优化，我们每 n 次更新 Aupdated，以便 GCN2 可以适应新的输入图。 最后，图邻接是通过对原始输入图进行加权平均（使用等式 4 更新）。
$$\begin{array}{r}{A}^{updated}=\lambda \ast A^{updated}+(1-\lambda )\ast A^{in}\end{array}\text{\hspace{1em}(4)}$$
       当我们有高质量的输入图时（例如，半监督学习基准中的那些，其连接基于数据集标签），我们凭经验确定 λ。 然而，在输入图有噪声的情况下（例如，在 [12] 中计算的用于动作识别的那些），我们通常设置 λ = 1，即不依赖于 GCN2 的输入图。 第 5 节提供了所有设置的详细信息。

4.2 使用 Triplet Loss 进行训练

       第 3 节 [57、12、24] 中描述的原始网络分别使用分类损失和 MSE（均方误差）损失来训练半监督和零样本学习网络。 为了帮助更新图结构，我们添加了三元组损失。 因此，最终框架使用三元组损失和任务特定损失的加权和进行训练，以使用权重因子 β 增加监督。 对于三元组损失，我们需要每个节点的正负集。 对于半监督学习，图中的每个训练节点都是一个带有类标签的数据样本。 所以我们可以使用 soft-triple loss [42]，它需要每个类的簇数作为超参数。 我们在验证集上凭经验确定这一点，值在第 5 节中提供。
       另一方面，需要明确定义动作的零/小样本学习中类节点的正邻居和负邻居。 我们依赖图中每个类的邻域来初始化这些集合，如下所示。 对于正集，我们简单地使用最接近输入 KG 中每个节点的前 N(=2) 个邻居。 然而，与三元组损失的情况一样，定义负集更具挑战性。如果我们只使用最远的邻居，使用 MSE 训练的下游任务网络已经实现了正负之间的良好分离，并且三元组损失的贡献可以忽略不计。 这意味着三元组损失对训练没有影响，邻接矩阵可以得到任意更新并导致退化解决方案。另一方面，如果负集太接近正集，负集中的一些节点可能会收缩，导致很大的罚值，不利于邻接矩阵的更新。 因此，我们使用验证集凭经验选择负集类的序数范围（详见第 6 节）。
       最后，我们取正负集的 GCN1 节点输出的平均值，得到正负向量。 那么，当正向量与当前节点之间的距离小于当前节点与负向量之间的距离一定幅度$\alpha （=0.1）$时，三元组损失为零。 在数学上，让 $H^{ref}$ 是当前参考节点的输出，$H^P$ 和 $H^N$ 分别是正集和负集节点的平均输出向量。 然后，$H^{ref}$和 $H^P$（或 $H^N$ ）之间的距离表示为 $d^P$ 和 $d^N$（等式 5）； 和三重态损失，$L_{triplet}$ 使用等式 6 计算。
$$\begin{array}{r}{d}^P=||H^{ref}-H^P|{|}_2,d^N=||H^{ref}-H^N|{|}_2\end{array}\text{\hspace{1em}(5)}$$
$$\begin{array}{r}{L}_{triplet}=max(d^P-d^N+\alpha ,0)\end{array}\text{\hspace{1em}(6)}$$

5 实验设置

       数据集。 我们使用 Citeseer、Cora 和 Pubmed 数据集 [49, 39] 进行半监督学习的实验，其中节点是文档，边是引用。 Citeseer 有 6 个类，Cora 有 7 个类，Pubmed 有 3 个类。 我们使用与 [24, 63] 相同的训练、测试和验证分割。对于零/少镜头动作识别，我们使用 Kinetics [22] 来预训练我们的特征提取模型，并作为构建图中的“附加节点”（有关详细信息，请参阅 [12]）。 我们使用 UCF101 [51] 和 HMDB51 [27] 作为我们的评估数据集。 动力学有 400 个类； UCF101有101个类，其中23个用于测试，78个用于训练； HMDB51 有 51 个类，其中 12 个用于测试，39 个用于训练。这些数据集拆分与 [12] 使用的相同。 我们在测试类中创建了 c 个类的 10 个随机子集，并且我们对所有 10 个子集的性能进行平均以进行验证。 然后我们选择在这个验证集上性能最好的模型，并报告整个测试集的结果。 对于 UCF101 数据集，c 是 20，对于 HMDB51 数据集，c 是 10。 有关数据集的更多详细信息在补充中。
       输入图。 接下来我们讨论我们在这项工作中研究的输入图。 对于半监督学习，我们使用与 [24] 相同的图，基于之前讨论的 Citeseer、Cora 和 Pubmed 数据集。 对于零/少镜头动作识别，我们使用 [12] 中使用的输入 KG。 我们在下面总结了这些 KG（并请读者参考 [9, 57] 以讨论用于这些任务的其他类型的 KG）。
       我们使用 action-KG（或 [12] 中的 KG1）进行零镜头学习； 在整个工作中称为 A-KG。 A-KG 节点使用sentence2vec [40] 表示动作短语，邻接矩阵中的边权重是对应节点特征之间的余弦相似度。 对于小样本学习，我们使用基于视觉特征的 KG（或 [12] 中的 KG3）； 统称为 V-KG。这些视觉特征是使用 I3D [3] 网络为每类五个随机样本提取的，并且这些特征被平均以生成 V-KG 的节点特征。与 A-KG 类似，边权重基于节点特征的余弦相似度。最后，我们还使用基于动词和名词的 KG（或 [12] 中的 KG2）显示结果，称为 VN-KG。动词和名词都从动作短语中提取，它们的sentence2vec 被用作两个独立KG 的节点特征。边缘连接再次基于节点特征的余弦相似度。在 [12] 之后，我们还展示了这些 KG 在不同设置下的组合结果，并证明我们的方法可以推广到不同的输入图公式。
       传递途径。 对于半监督学习，我们使用两层网络，其中中间输出用于更新图连接。 所有三个数据集的学习率为 0.005。 我们凭经验确定Pubmed 和 Cora的软三重损失的每类聚类数为 2，Citeseer 为 10。 软三重损失的其余超参数与 [42] 相同。 对于所有数据集，等式 4 中的 λ 参数为 0.8。
       对于零/少镜头动作识别，我们使用在 Kinetics 上预先训练的 I3D [3]，并且仅微调下游数据集上的最后一个分类器层（分别在 UCF101 和 HMDB51 上）直到收敛。 我们对 GCN1 使用一层，对 GCN2 使用五层，其中最后一层用于融合 GCN，用于使用多个 KG 的设置。 所有实验的学习率为 0.001，除了 UCF101 的小样本学习，其中学习率为 0.00005。 为了计算 MSE 损失，我们使用基于特定数据集节点（HMDB51 和 UCF101）和动力学节点的损失加权求和。 除了 HMDB51 A-KG + V-KG + VN-KG 为 0.5（凭经验确定）之外，等式 4 中的 λ 对于所有零样本/少样本 KG 都是 1.0。 对于 HMDB51 A-KG，我们使用 GCN2 的最终输出来计算 Aupdated（相对于 GCN1）并且没有三元组损失。 有关传递途径的更多详细信息在补充中。

6 定量结果

6.1 半监督学习

       我们在表 1 中展示了 Cora、Citeseer 和 Pubmed 数据集的半监督学习结果。我们与多种最先进的方法进行了比较，包括 GLCN [21] 和 GLNN [10] 等图学习方法。 GCN* 是我们在 PyTorch 环境中实现的 GCN [24]，有 256 个中间通道，我们得到的基线结果略有不同。由于我们的方法建立在此基线上，因此我们也报告了这些结果，以进行直接比较。 我们的方法在 Cite seer 和 Pubmed 数据集上都优于所有其他方法。 GLCN 在 Cora 数据集上表现最好，但他们在 GCN 基线上的结果是 82.9%，图学习后他们的结果是 85.5%，所以相对性能增益是 2.6%。 我们的基线 GCN 结果是 80.0%，图学习后我们的结果是 83.6%，这意味着 3.6% 的相对增益。

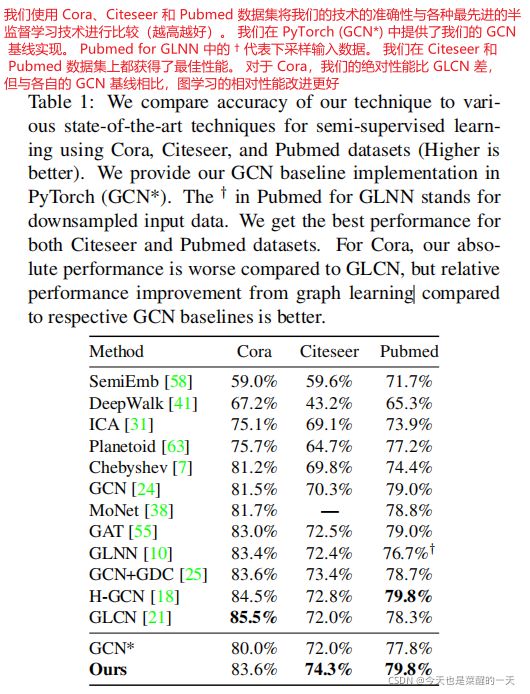
       消融分析。 我们在表 2 中的 Pubmed 验证集上使用等式 4 中的不同 λ 值报告结果。我们观察到 $\lambda =0.8$ 实现了最佳性能，并在所有半监督实验中使用它。 补充资料中提供了额外的实验和结果。

6.2 零次/少次动作识别

       我们在表 3 中与 [12] 的零和少镜头动作识别结果进行比较。 这些结果针对 UCF101 和 HMDB51，使用三种不同的输入图配置：A-KG、V-KG 和 A-KG + VN-KG +V-KG。 对于 UCF101 和 HMDB51，度量是平均准确率，它是所有类的平均分类准确率。 可以观察到，我们在训练期间更新图结构的方法明显优于 [12]。

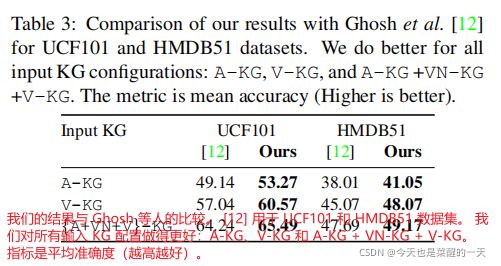
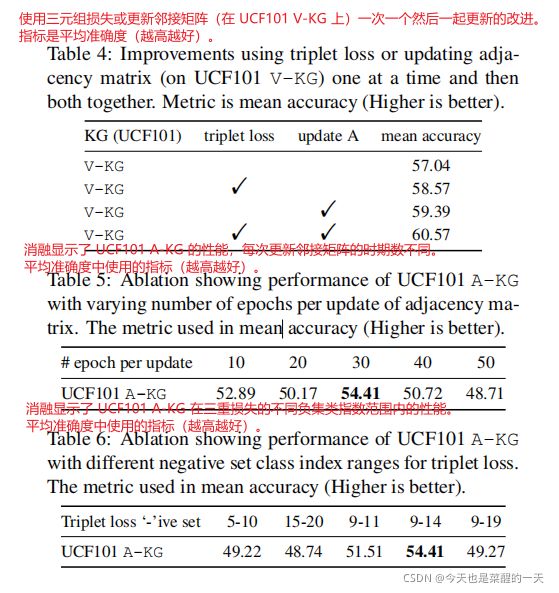
       消融分析。 我们首先分析了我们的方法对更新邻接矩阵 A 和表 4 中的三元组损失公式的贡献（在 UCF101 上使用 V-KG）。 我们表明，这两种贡献都是单独有效的，并且相互补充。 接下来，我们研究与我们的建议相关的两个超参数——（a）在更新 A（n）之前改变时期的数量，以及（b）三元组损失的负类的不同序数范围。 结果分别列于表5和表6中。 对于这些，我们使用 10 次随机选择的 20 个测试类子集的平均值。 我们在每次更新 30 个 epoch 和负集范围 [9, 14] 时获得最佳性能。

       与最先进的零样本学习的比较。 最后，我们与最先进的零样本学习方法进行比较。 请注意，我们不能对少样本学习进行类似的比较，因为我们不像其他论文那样遵循情节学习管道。 特别是，我们与 ESZSL [46]、DEM [66]、TS GCN [9]、GLCN [21]、[12]、[33]、UR [69]、Action2vec [14] 和 TARN 进行比较 [1]。 有关这些方法的更多详细信息，请参阅补充文件。我们对 UCF101 和 HMDB51 数据集进行评估并报告平均准确度。 我们在表 7a 中提供了整个测试集的结果，包括 UCF101 和 HMDB51，以及表 7b 中先前论文使用的 20/81 分割。 对于后者，我们从 UCF101 测试类中随机选择 20 个类 10 次，并平均输出性能并报告所有运行的平均分数。 我们在所有三种情况下都优于最先进的技术，进一步强调了更新零样本方法的图结构的重要性。

7 讨论

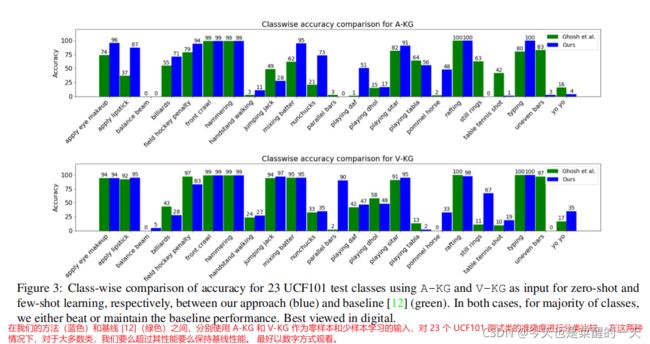
       类性能表现。 在图 3 中，我们展示了我们的方法与以 A-KG 和 V-KG 作为输入的 UCF101 测试类的 [12] 之间的类性能比较。 对于使用 A-KG 的零样本学习，我们的技术优于大多数类（23 个中的 12 个）的基线，例如“应用眼妆”、“应用口红”、“台球”、“双节棍”和“玩达夫”。 在某些情况下（23 个中的 7 个），例如“静止环”、“乒乓球击球”、“不均匀条”，我们更新后的图表表现更差。 稍后讨论“静环”类的解释（在图 5 中）。 对于使用 V-KG 的小样本学习，我们在 12 上表现更好，在 6 上表现更差，并且类似于 5 类上的固定输入图。

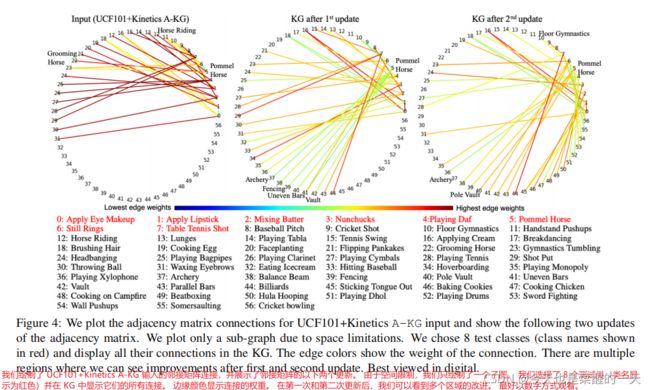
       图更新的定性结果。 图 4 显示了基于 A-KG 的 UCF101 和 Kinetics 的 57 个选定节点之间的图连接。这些节点是所选 8 个测试类的邻居（类名显示在
红色的）。边缘权重由颜色条中的边缘颜色表示。在这个颜色条中，蓝色代表最低的边缘权重，红色代表最高的边缘权重，中间有绿色和黄色。左边的可视化是输入邻接矩阵，中心是在第 30 个时期的第一次更新之后，右边是在第 60 个时期的第二次更新之后。图 4 显示了基于 A-KG 的 UCF101 和 Kinetics 的 57 个选定节点之间的图连接。这些节点是选定的 8 个测试类（类名称显示为红色）的邻居。边缘权重由颜色条中的边缘颜色表示。在这个颜色条中，蓝色代表最低的边缘权重，红色代表最高的边缘权重，中间有绿色和黄色。左边的可视化是输入邻接矩阵，中心是在第 30 个时期的第一次更新之后，右边是在第 60 个时期的第二次更新之后。更新改进输入KG的例子有很多，但由于空间限制，我们这里只讨论一个特定的节点（更多例子请参考补充）。 对于“鞍马”（体操运动员的动作），我们在输入 KG 中看到多个错误连接，因为这个 KG 是基于词嵌入的。 由于名称中存在“马”一词，它将“鞍马”与“美容马”和“骑马”联系在一起。 第一次更新后，这些连接将被删除，但它会创建与“射箭”和“击剑”等不正确的类的连接。 它有一些正确的连接，比如“Vault”，“Uneven bar”； 但是由于各种连接的标准化，权重很低。 在第二次更新后，许多这些连接（如“射箭”）被删除，权重增加到“地板体操”和“撑竿跳高”等连接。 因此，每次更新后，KG 总体上都会有所改善。

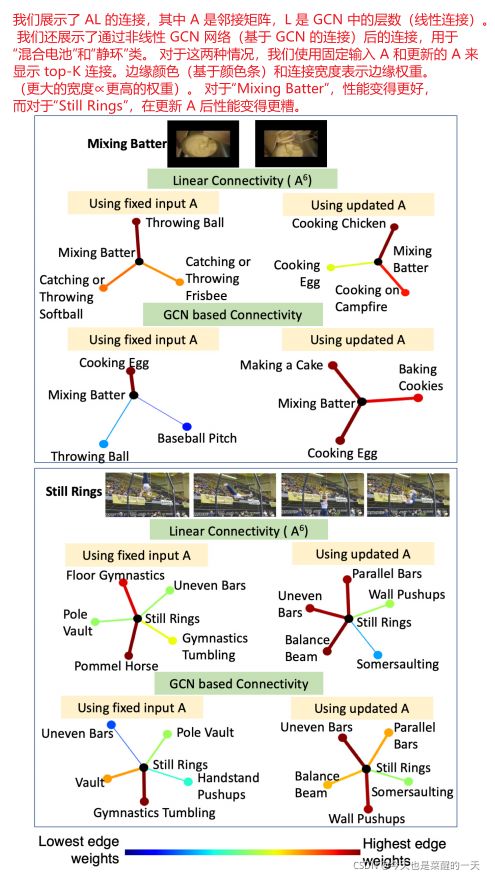
       可视化重要的连接。 图 5 显示了与 GCN 网络相关的重要图连接。 GCN 有多层，每一层都涉及卷积、邻接矩阵乘法和非线性。该系统的线性等价物是 $A^L$，其中 $L$ 是 GCN 中的层数，A 是邻接矩阵。我们显示 $A^L$ 中的前 $N$ ​​个邻居，其中 A 来自输入和更新的两个测试类的邻接矩阵：图 5 中标记为线性连接的“混合击球手”和“静环”。当我们的方法更新了邻接矩阵时，我们还在 GCN 操作之后可视化最近的邻居。我们提出了一种新的可视化技术，受到 [65] 的启发，该技术将输入图像的一部分遮挡起来以理解 ConvNets。如果 GCN 操作用 G 表示，GCN 的输入是 KG K，则原始输出概率为 $O=G(K)\times f_{vid}$，其中 fvid 是 C 类视频的特征向量。 接下来，我们通过删除与一个输入节点 ni 的连接将 $K$ 修改为 $K-n_i$，新的输出由 $O_{new}=G(K-n_i)\times f_{vid}$ 给出。那么，节点 $n_i$ 和正确的输出类节点 $C$ 之间连接的重要性由等式 7 给出，其中变化越大，连接越重要。
$$\begin{array}{r}|O-O_{new}|=|(G(K)-G(K-n_i))\times f_{vid}|\end{array}\text{\hspace{1em}(7)}$$
       我们展示了使用这种方法提取的基于 GCN 的连通性，在图 5 中使用输入和更新的邻接矩阵，针对“混合击球手”和“静环”这两个类别。边缘颜色和宽度代表连接的重要性或权重（宽度越大意味着边缘权重越高）。更新的基于邻接矩阵的连通性对于“混合击球手”变得更好，对于“静止环”变得更糟。对于“混合面糊”，基于词嵌入的 KG 将“面糊”与“棒球”类（如“投掷球”、“棒球场”等）相关联，而我们更新的 KG 正确地将“混合面糊”与“烹饪”等烹饪类相关联鸡蛋”和“做蛋糕”。另一方面，对于“Still ring”，原始 KG 有“Pole Vault”和“Gym nastics tumbling”作为一些顶级邻居，而更新后的 KG 有“平衡梁”、“不均匀杆”和“平行杆”酒吧”作为顶级邻居。问题是这些更类似于“Pommel horse”测试类，因此更新后大多数“Still ring”视频被预测为“Pommel horse”。在少镜头场景中，此问题的一种可能解决方案是对邻接矩阵进行选择性更新，其中仅更新那些节点的邻居，从而获得更好的性能。

8 结论

       我们提出了一种使用可以遵守图中度数约束的三元组损失自适应更新基于 GCN 的公式中的邻接矩阵的方法。 我们分析并定性地展示了图连接如何随着更新而变化。 受先前在 ConvNets 上工作的启发，我们将 GCN 操作之后以及输入处的各个连接的重要性可视化。 我们在用于半监督学习和零/少镜头动作识别的多个基准数据集上的性能明显优于大多数最先进的技术。
       致谢。 这项工作得到了空军的支持，通过小型企业技术转让 (STTR) 第一阶段 (FA865019P6014) 和第二阶段 (FA864920C0010) 以及国防高级研究计划局 (DARPA) 航行计划 (W911NF2020009)。