Dueling DQN论文笔记
Dueling DQN论文笔记
- Abstract
- Background
- Technology
-
- Model Architecture
- Summary
参考:https://www.cnblogs.com/pinard/p/9923859.html
Abstract
与Double DQN优化目标Q值的计算、Prioritized Experience Replay优化经验回放的采样概率不同,该论文通过优化神经网络结构的方式使算法表现更佳。新的神经网络作为两个估计器分别近似互相独立的量:状态值 V ( s ) V(s) V(s)与动作优势值 A ( s , a ) A(s,a) A(s,a),并最终组合成动作-状态值 Q ( s , a ) Q(s,a) Q(s,a)。这种分解的主要优点在于可以不对底层的强化学习算法进行任何改动,就能应用于各种动作情况下。并且该网络进行优势更新要比Q学习收敛更快,当问题存在类似或冗余动作时快速地找到最优策略,同时这种结构可以与其他多种无模型的RL算法结合使用。
Background
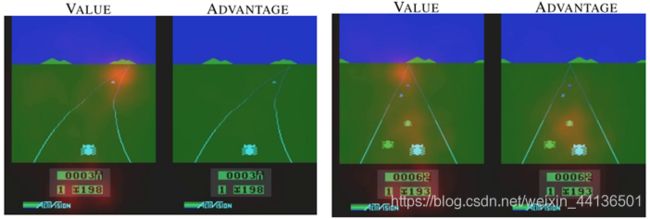
在上述赛车环境中,当赛道上无其他车辆时原本的DQN算法会对当前所处的状态进行判断并做出动作,然而此时玩家做出任何动作都对得分没有任何影响:可以认为这种情况下的得分只与状态有关,只有当对面来车时才有必要做出动作。论文提出的Dueling DQN网络结构通过分别估计状态值 V ( s ) V(s) V(s)与动作优势值 A ( s , a ) A(s,a) A(s,a),使得状态估计器学会关注道路,而只有在正前方有车的时候动作优势估计器才会注意,避免碰撞;因此减弱了动作空间的冗余对训练效果的影响,加快网络收敛。
Technology
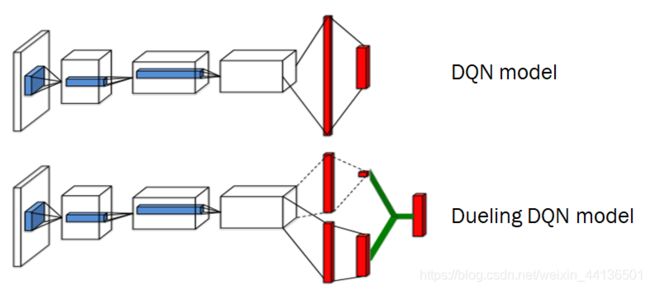
可以看到上面的DQN网络模型只有一个输出,就是每一个动作的状态-动作值 Q ( s , a ; θ ) Q(s,a;\boldsymbol \theta) Q(s,a;θ),而Dueling DQN则拆成了状态值 V ( s ; θ , β ) V(s;\boldsymbol \theta, \boldsymbol \beta) V(s;θ,β)和每个动作的优势值 A ( s , a ; θ , α ) A(s,a;\boldsymbol \theta, \boldsymbol \alpha) A(s,a;θ,α)。
图中Dueling网络可以分为三部分,红色的全连接层前是共同部分,用参数 θ \boldsymbol \theta θ来表示;上面的是状态估计器,以参数 β \boldsymbol \beta β来表示并输出标量形式的状态值 V ( s ; θ , β ) V(s;\boldsymbol \theta, \boldsymbol \beta) V(s;θ,β);下面的是动作优势值估计器,以参数 α \boldsymbol \alpha α来表示并输出动作空间大小的向量形式的动作优势值 A ( s , a ; θ , α ) A(s,a;\boldsymbol \theta, \boldsymbol \alpha) A(s,a;θ,α);而在网络的最后则是将得到的状态值 V ( s ; θ , β ) V(s;\boldsymbol \theta, \boldsymbol \beta) V(s;θ,β)与动作优势值 A ( s , a ; θ , α ) A(s,a;\boldsymbol \theta, \boldsymbol \alpha) A(s,a;θ,α)结合,得到与上面DQN网络相同的输出:状态-动作值 Q ( s , a ; θ , α , β ) Q(s,a;\boldsymbol \theta, \boldsymbol \alpha,\boldsymbol \beta) Q(s,a;θ,α,β)。
而这种优势分解可以由贝尔曼方程得到,这里给出优势公式:
Q ( s , a ; θ , α , β ) = V ( s ; θ , β ) + A ( s , a ; θ , α ) Q(s,a;\boldsymbol \theta, \boldsymbol \alpha,\boldsymbol \beta)=V(s;\boldsymbol \theta, \boldsymbol \beta)+A(s,a;\boldsymbol \theta, \boldsymbol \alpha) Q(s,a;θ,α,β)=V(s;θ,β)+A(s,a;θ,α)
从直观上看,值函数 V ( s ) V(s) V(s)衡量的是处于特定状态 s s s的情况有多好。然而, Q Q Q函数衡量的是在这种状态下选择特定行动的值。优势函数从 Q ( s , a ) Q(s,a) Q(s,a)中减去状态值,从而获得每个行为重要性的相对度量。其中 θ \boldsymbol \theta θ是网络公共部分的参数, α \boldsymbol \alpha α是估计优势函数部分的参数, β \boldsymbol \beta β是估计状态值函数部分的参数。
尽管上述公式已经可以使用,但是由于实际训练中它无法明确某时刻状态价值 V V V和动作优势 A A A各自对 Q Q Q值的贡献,从而不能合适地调整两个估计器参数。为了体现出状态价值 V V V和动作优势 A A A贡献的唯一性,实际将动作优势 A A A再减去其均值(增加 A A A的平均值为0的限制),使用以下公式:
Q ( s , a ; θ , α , β ) = V ( s ; θ , β ) + ( A ( s , a ; θ , α ) − 1 ∣ A ∣ ∑ a ′ ∈ A A ( s , a ′ ; θ , α ) ) Q(s,a;\boldsymbol \theta, \boldsymbol \alpha,\boldsymbol \beta)=V(s;\boldsymbol \theta, \boldsymbol \beta)+(A(s,a;\boldsymbol \theta, \boldsymbol \alpha)-\frac1{\vert \mathcal A\vert}\sum_{a'\in \mathcal A}A(s,a';\boldsymbol \theta, \boldsymbol \alpha)) Q(s,a;θ,α,β)=V(s;θ,β)+(A(s,a;θ,α)−∣A∣1a′∈A∑A(s,a′;θ,α))
Model Architecture
Dueling神经网络具体结构:3个卷积层接2个全连接层。
第一层卷积层:32个8 ∗ \ast ∗ 8滤波器,步长4
第二层卷积层:64个4 ∗ \ast ∗ 4滤波器,步长2
第三层卷积层:64个3 ∗ \ast ∗ 3滤波器,步长1
第四层全连接层:第三层卷积层后同时接上2个全连接层,均为512单元(此时分别输出状态流与优势函数流)
第五层全连接层:状态流与优势函数流各自接上一个全连接层(状态流全连接层输出一个标量,优势函数流全连接层输出与动作空间大小相同的向量)
使用特殊的聚合层将状态价值与优势函数组合。
在所有相邻层之间插入整流器非线性
因为后向传播时优势流和状态流都会将梯度传播到最后一个卷积层中,所以将进入最后一个卷积层的联合梯度重新缩放为 1 2 \frac1{\sqrt{2}} 21倍 。(???不理解)可以增加稳定性。
Summary
该论文引入一种新的神经网络结构,并在Deep Q Network中将 Q ( s , a ) Q(s,a) Q(s,a)函数分解为状态价值 V ( s ) V(s) V(s)与动作优势值 A ( s , a ) A(s,a) A(s,a),同时共享一个公共的特征学习模块。并且该结构可以与其他RL算法结合,在Atari 2600游戏中取得比现有(2016年)深度RL方法更好的表现。
该论文是在DQN、DDQN、重要性采样基础上提出。
存在问题:状态价值与优势函数关于Q的组合不是唯一的,因此会导致较差的性能。
解决:强制优势函数估计器在所选择的动作优势为0,也就是让网络的最后一个模块实现正向映射。以减去最大值或者平均的方式使得状态价值与最优优势函数的组合唯一。平均的方式可以增加优化的稳定性不会改变优势函数的相对rank,且比其他的方式效果都要更佳,所以论文实验都采取平均的方式进行优化。
神经网络只需按照DQN的步骤正常进行反向传播就可以得到状态价值与优势函数,不需要额外的监督与算法修改。
剪切梯度使其范数小于等于10。(这种方法可以使得策略优于没有剪切的策略)
Dueling结构专注于状态值的特性相对于DQN内Q值差距小导致最优动作容易变更的特点可以得到更加稳健的策略。
DRL、连续状态离散动作问题、单智能体、off-policy、值估计、改进网络模型