【minimal problem】资料整理

minimal problem

use as few data as to generate a system of algebraic

equaIons with a finite number of soluIons

使用尽可能少的数据来生成代数系统
解数有限的方程

以往工作

基于神经网络解一元高次方程
代码实战：解低次方程
代码实战：解高次方程

主要论文

Principles of Solving Minimal Problems（ICCV2015）

Minimal problem:
论文链接：

http://cmp.felk.cvut.cz/minimal-iccv-2015/present/SMP-2015-Principles-Pajdla.pdf

1. 问题公式——>代数方程
2. 解代数方程
   
   单一未知数——特征值
   
   
   余数明确定义的除数，不依赖于除数的顺序
   Groebner basis

https://zhuanlan.zhihu.com/p/262906557

Grobner基的功能类似于结式和特征列，可以用于解代数方程组。Grobner基不一定是三角列，但Grobner基的消元性质（Thm7.3.4）确保了变元的分离。所以可以从纯字典序的Grobner基求得一组多项式方程的解。所以我们需要计算最大公因式
线性方程——代数方程

通过构造Groebner basis求解多项式方程
1888：
大卫希尔伯特：有限性定理

1965：
Bruno Burchberger: Groebner bases
Computational procedure for solving systems
of polynomial equations
(Extremely simple: 20 lines of Maple code!)
求解系统的计算程序
多项式方程
（极其简单：20 行 Maple 代码！）
Gröbner基——Buchberger的发现，却以他导师的姓命名
A dynamic F4 algorithm to compute Gröbner bases

1998：
Hans Stetter：乘法矩阵
通过特征向量的稳定数值过程

Automa’c Generator of Minimal Problem(ECCV2008)

ECCV 2008

https://xueshu.baidu.com/usercenter/paper/show?paperid=de5e30310c5378bd033b9f0ba90e4da4&site=xueshu_se

Automatic Generator of Minimal Problem Solvers

斯图姆定理：

https://baike.baidu.com/item/%E6%96%AF%E5%9B%BE%E5%A7%86%E5%AE%9A%E7%90%86/18881160

https://zhuanlan.zhihu.com/p/164729380

代码：

https://github.com/PavelTrutman/Automatic-Generator/tree/development

% 
% P6P rolling shutter (eliminated)
function [eq, known, unknown, kngroups, cfg, algB] = minimal_rolling_shutter_generator_linear_I_planar()

g1 = transpose(gbs_Vector('g1', 8));
g2 = transpose(gbs_Vector('g2', 8));
g3 = transpose(gbs_Vector('g3', 8));
g4 = transpose(gbs_Vector('g4', 8));
g5 = transpose(gbs_Vector('g5', 8));
g6 = transpose(gbs_Vector('g6', 8));



syms v_1 v_2 v_3 w_1 w_2 w_3;


mon = [v_3*w_3 v_1 v_2 v_3,  w_1, w_2, w_3, 1];

cfg = gbs_InitConfig();

clear eq;


% g1(1) = 1
% g2(1)=0
% g3(1)=0
% g4(1)=1
% g5(1)=0
% g6(1)=0
% 
% g1(5)=0
% g2(5)=0
% g3(5)=0
% g4(5)=0
% g5(5)=0
% g6(5) = 1;
% 
% g1(6)=0
% g2(6)=0
% g3(6)=0
% g4(6)=0
% g5(6)=-1
% g6(6)=0
% 
% g1(7) = 0
% g2(7) = -1
% g3(7) = 1
% g4(7) = 0
% g5(7)=0
% g6(7)=0


eq(1) = v_1*w_1 + g1*transpose(mon);
eq(2) = v_1*w_2 + g2*transpose(mon);
eq(3) = v_2*w_1 + g3*transpose(mon);
eq(4) = v_2*w_2 + g4*transpose(mon);
eq(5) = v_3*w_1 + g5*transpose(mon);
eq(6) = v_3*w_2 + g6*transpose(mon);


% g1 = transpose(gbs_Vector('g1', 8));
% g2 = transpose(gbs_Vector('g2', 8));
% g3 = transpose(gbs_Vector('g3', 8));
% g4 = transpose(gbs_Vector('g4', 8));
% g5 = transpose(gbs_Vector('g5', 8));
% g6 = transpose(gbs_Vector('g6', 8));

unknown = {'v_1' 'v_2' 'v_3' 'w_1' 'w_2' 'w_3'};
vars = transpose([g1(:); g2(:); g3(:); g4(:); g5(:); g6(:)]);
known = {};
for var = vars
    known = [known {char(var)}];
end    

% create symbolic vars
for mon = unknown
    eval(['syms ' char(mon) ';']);
end

%cfg.eqinstance = R6P_planar_inst(cfg);

% call code generator
kngroups = ones(8,1)*[1 2 3 4 5 6];
%[res export] = gbs_CreateCode('p6p_rs_lin_I_planar', eq, known, unknown, kngroups);
algB = [];

%[A symcoefs] = rsSolver('imu3pr_peieg.m', eq, 'tan', unknown, known, kngroups);
end

Learning to Solve Hard Minimal Problems(CVPR2022)

https://theigrams.github.io/zjblog/2022/07/18/learning-to-solve-hard-minimal-problems.html

但是这篇论文的代码和结果不算特别好看，作为参考。

minimal problem

当从图像数据计算几何模型时会出现计算机视觉中的最小问题
这个网站里有比较全面的收录：

https://cmp.felk.cvut.cz/~kukelova/minimal/index.php

作者报告
github

https://www.docin.com/p-1684946348.html

4-pt absolute pose problem with unknown focal length (P4Pf)

从四个 3D 参考点的图像确定具有未知焦距的透视相机位姿的通用解决方案。

A general solution to the P4P problem for camera with unknown focal length（CVPR2008）

论文链接：
A general solution to the P4P problem for camera with unknown focal length

5-pt relative pose problem

从五个图像点对应估计两个完全校准相机的相对位姿。

相关论文

更多内容

6-pt focal length problem

8-pt radial distortion problem

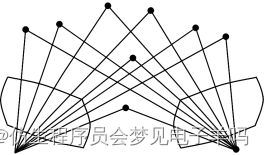
9-pt radial distortion problem
从九个图像点对应的具有不同径向畸变的两个部分校准相机的对极几何和单参数径向畸变模型的同时估计。

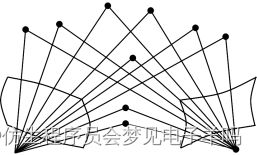
3-view triangulation problem
三视图L2-最优三角剖分问题。

网络平台

百度学术

https://xueshu.baidu.com/s?wd=minimal+problem&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8&sc_hit=1

CSDN

CVPR 2008 papers

Byr¨od, M., Kukelova, Z., Josephson, K., Pajdla, T., Astr¨ ˚ om, K.:
Fast and robust numerical solutions to minimal problems for cameras
with radial distortion. In: CVPR 2008 (2008)

Two minimal problems for cameras with radial distortion

https://schlr.cnki.net/en/Detail/index/GARJ2021_2/XQSPB7D061D4B0264289C699D9AA81C39AB8

arxiv

https://arxiv.org/search/?query=algorithm+to+compute+Gr%C3%B6bner+bases&searchtype=all&source=header

A clever elimination strategy for efficient minimal solvers

A fast minimal solver for absolute camera pose with unknown focal length and radial distortion from four planar points

这篇值得深读

GPU-Based Homotopy Continuation for Minimal Problems in Computer Vision

多项式⽅程组在计算机视觉中经常出现，尤其是在多视图⼏何问题中。解决这些
系统的传统⽅法通常旨在消除变量以达到单变量多项式，例如，⽤于 5 点姿态估
计的⼗阶多项式，使⽤巧妙的操作，或更⼀般地使⽤ Grobner 基础、结果和消除
模板，导致多视图⼏何和其他问题的成功算法。

Optimizing Elimination Templates by Greedy Parameter Search

矩阵运算参考