论文阅读 - Is Space-Time Attention All You Need for Video Understanding?

1 概述

这篇论文是在vision transformer的基础上，在时间维度进行了attention，将图像分类拓展到了视频分类。这也是第一个完全抛弃CNN，只用transformer搭建整个网络的视频分类模型。

作者在文中说到，之所以进行这种只用transformer的尝试，是有三点原因：
（1）tranformer在NLP领域取得了巨大的成功，视频和文本一样，某些动作需要有上下文才能进行准确的分类；
（2）CNN有很强的inductive bias，其一，卷积利用卷积核的方式告诉了卷积网络，每个像素点和它周围的像素点有很大的关联；其二，卷积核权重共享的机制告诉了卷积网络，图像当中的物体移动之后，仍旧是相同的物体。transformer其实也有一些inductive biases，比如必须要根据相似度来融合信息，但这种biases比较weak。同时CNN只能处理感受野之内的信息，如果需要看图片的全局信息，就必须要用很深的网络，而很深的网络又需要大量的数据和大量的算力。
（3）transformer需要的算力小，而且可以适用于比较长的视频，比如1分钟以上的，甚至是7分钟左右的。

在将空间维度的transformer和时间维度的transformer进行结合时，作者也尝试了很多方法，最终发现将时间和空间和attention分开计算的"divided space-time attention"是效果最好的。

2 模型结构

2.1 模型输入

模型的输入为从视频片段中等分抽取的$F$帧，表示为$X$，$X$的shape为$H\times W\times 3\times F$。比如一个2s，fps为24的视频片段，当$F=8$时，就会取$[0,6,12,18,24,30,36,42]$这几帧作为一个序列来输入。$F$在论文中的取值是$[8,32,64,96]$这几种，没有特殊说明的话，就是$F=8$。

输入的每一帧会先经过resize和crop成为一个预先设置好的模型接受的输入尺寸，一般是$224\times 224$，然后每一帧都会被切成多个patches，每个patch的尺寸为$P\times P$，$P$一般取16。切成多个patches之后的图像就如图2-2中的图片示意的那样，一共会被切成$N$个patch，$N=HW/P^2$。

切割后的每一个patch可以表示为$x_{(p,t)}$，其中$p=1,...,N$表示属于一帧中的第几个patch，$t=1,...,F$表示第几帧。

最后，每个patch会经过一层embedding，得到

$$z_{(p,t)}^{(0)}=E{x}_{(p,t)}+e_{(p,t)}^{pos}\text{\hspace{1em}(2-1)}$$

其中，$z_{(p,t)}^{(0)}$表示第0层，第$t$帧的第$p$个patch的embedding结果，$E$是一个可以学习的大的矩阵，$e_{(p,t)}^{pos}$是position embedding，也是一个可以学习的参数。

同时，也加入了一个特殊的可学习的向量$z_{(0,0)}^{(0)}$，这个向量对应的输出会被用作最终分类网络的输入。这部分和vision transformer基本一致，熟悉vision transformer的话，对这里的理解就不会有问题。

2.2 attention模块

首先，要得到每个patch的query，key和value。

$$\{\begin{array}{ll}& q_{(p,t)}^{(l,a)}=W_Q^{(l,a)}LN(z_{(p,t)}^{(l-1)})\\ & k_{(p,t)}^{(l,a)}=W_K^{(l,a)}LN(z_{(p,t)}^{(l-1)})\\ & v_{(p,t)}^{(l,a)}=W_V^{(l,a)}LN(z_{(p,t)}^{(l-1)})\end{array}\text{\hspace{1em}(2-2)}$$

其中，$LN()$表示LayerNorm，$a=1,...,A$表示第$a$个head。

然后开始attention，这里相比图片的transformer多了时间的维度，所以如果直接全都做attetion的话，计算量会非常大，每个patch需要计算$N\times F+1$次attention，如下式$(2-3)$所示。

$${\alpha }_{(p,t)}^{(l,a)}=SM(\frac{(q_{(p,t)}^{(l,a)}{)}^T}{\sqrt{D_h}}\cdot [k_{(0,0)}^{(l,a)}\{k_{(p^{\prime },t^{\prime })}^{(l,a)}{\}}_{p^{\prime }=1,...,N|t^{\prime }=1,...,F}])\text{\hspace{1em}(2-3)}$$

其中$SM$表示softmax，$D_h=D/A$表示每个head分到的维度，$D$是embedding的维度。中括号里的$k$表示$k$的可选集合。

为了减小attention的计算量，作者想出了如下图2-1所示的多种attention的方式。

图2-1 多种attention的方式网络结构示意图

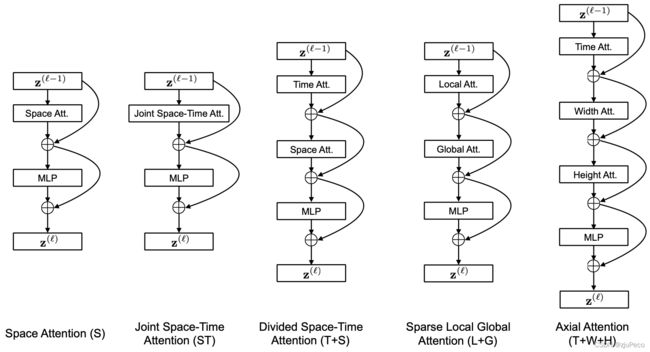
图2-1中，中间这种将时间的attention和空间的attention分开计算的方式，效果最好，也是作者最后使用的，称为"divided space-time attention"。这种方法只需要计算$N+F+2$次attention即可，如下式$(2-4)$所示。

$$\{\begin{array}{ll}{\alpha }_{(p,t)}^{(l,a)time}& =SM(\frac{(q_{(p,t)}^{(l,a)}{)}^T}{\sqrt{D_h}}\cdot [k_{(0,0)}^{(l,a)}\{k_{(p^{\prime },t^{\prime })}^{(l,a)}{\}}_{t^{\prime }=1,...,F}])\\ {\alpha }_{(p,t)}^{(l,a)space}& =SM(\frac{(q_{(p,t)}^{(l,a)}{)}^T}{\sqrt{D_h}}\cdot [k_{(0,0)}^{(l,a)}\{k_{(p^{\prime },t^{\prime })}^{(l,a)}{\}}_{p^{\prime }=1,...,N}])\end{array}\text{\hspace{1em}(2-4)}$$

注意，这里为了书写方便才这么写的，但是我们要心里清楚，time和space所用到的$q$，$k$和$v$是不同层的，是不同的。

其他几种方式的attention也是大同小异，不了解也没关系，下图2-2是将在不同方式下第t帧的左上角的patch做attention时，用到的前后帧及自身的patch的示意图。

图2-2 多种attention的方式图片示意图

从图2-2中可以看出，"divided space-time attention"在时间的维度上，只考虑了对应位置的patch，因此，不难想象，它对于更依赖于时间去辨别的类别，效果要差一些。

有了attention之后，结合value可以得到一个attention的最终输出

$$s_{(p,t)}^{(l,a)}={\alpha }_{(p,t),(0,0)}^{(l,a)}{v}_{(0,0)}^{(l,a)}+\sum _{p^{\prime }=1}^N\sum _{t^{\prime }=1}^F{\alpha }_{(p,t),(p^{\prime },t^{\prime })}^{(l,a)}{v}_{(p^{\prime },t^{\prime })}^{(l,a)}\text{\hspace{1em}(2-5)}$$

这个输出再经过一个MLP，搞个残差，就得到了一层的输出，如下式(2-6)所示。之前说的time和space用的是不同层的，就是这里的不同。

$$\{\begin{array}{ll}{z}_{(p,t)}^{\prime (l)}& =W_O[s_{(p,t)}^{(l,1)},..,s_{(p,t)}^{(l,A)}{]}^T+z_{(p,t)}^{(l-1)}\\ z_{(p,t)}^{(l)}& =MLP(LN({z^{\prime }}_{(p,t)}^l))+{z^{\prime }}_{(p,t)}^{(l)}\end{array}\text{\hspace{1em}(2-6)}$$

2.3 分类模块

当得到所有层的输出之后，分类用的就是用的之前在输入中加的特殊的向量对应的输出。

$$y=LN(z_{(0,0)}^{(L)})\text{\hspace{1em}(2-7)}$$

拿$y$去过分类器就行了，分类器可以是一个全连接。

这里有一个细节值得一提，在预测的时候，作者用了三种不同crop的方式，过模型之后取平均。crop的方式是top-left, center和bottom-right，这一步是在模型输入的时候做的。比如把图片resize到$256\times 256$之后，再用这种方式crop到$224\times 224$。

3 模型分析

3.1 不同attention方式

如下表3-1所示，不同的attention的方式，所需要的参数量不同，在数据集K400和SSv2上的表现也不同。总体来说"divided space-time"的效果最好。

表3-1 不同attention方式效果对比表

这里值得一提的是，只有space attention的模型在K400上也有比较好的表现，但是在SSv2上效果显著下降，这一方面说明SSv2数据集的类别更需要时间维度的信息，另一方面也说明了time attention的确对时间维度的信息有较大贡献。

3.2 不同的输入

作者对比了不同的输入尺寸和不同的输入帧数下，"joint space-time"和"divided space-time"所需要的算力的对比。"divided space-time"显然需要的算力更小，这也与理论一致。

图3-1 不同的输入算力对比

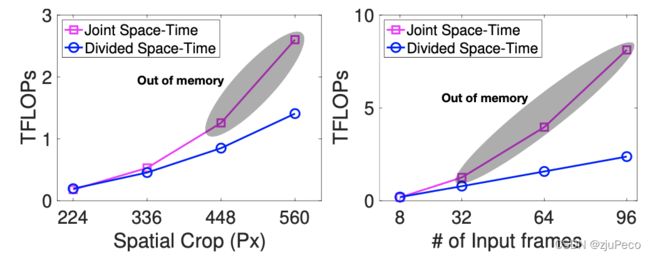
不同的输入，对TimeSformer的最终效果也有一定的影响，更大的输入尺寸，更多的输入帧数，代表着更高的准确率。不过尺寸，会带来负收益。

图3-2 不同的输入准确率对比

3.3 不同的模型

作者对比了不同模型在相同数据集上的表现，如下表3-2所示。可见TimeSformer需要的训练时间更少，准确率也更高。虽然TimeSformer的参数量远大于其他模型，但是其需要的算力更小，这就是纯transformer相较于CNN的优势。

表3-2 不同的模型效果对比表

同时也不难看出，在更大的数据集上进行pretrain之后，模型的效果也会变得更好。

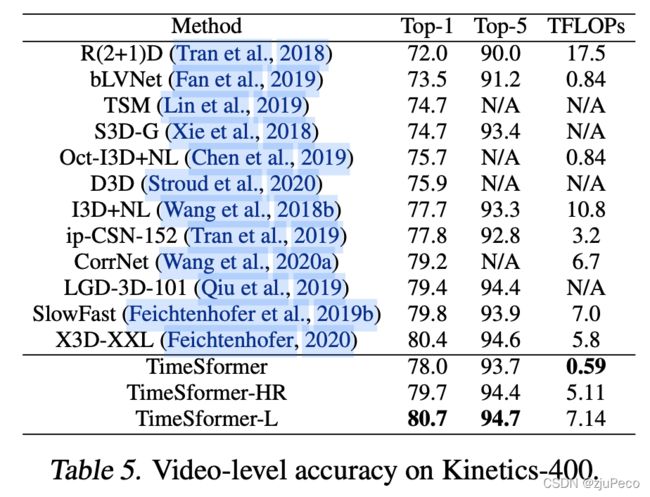
除此之外，作者也对比了一些现在state of art的模型在不同数据集上的表现，其结果如下表3-3，表3-4和表3-5所示。总的来说就是准确率更高，算力更小，不多说了。不过在依赖于时间特征的数据集上，并不是最好的模型。

表3-3 不同的模型在K400效果对比表

表3-4 不同的模型在K600效果对比表

表3-5 不同的模型在SSv2和Diving-48**效果对比表

3.4 不同的预训练数据

在不同的图片预训练数据下，更大的数据集，会让模型在K400上有更好的表现，但在SSv2上却见效甚微，这主要是因为SSv2更需要时间维度的特征来区别。

表3-6 不同的预训练数据效果对比表

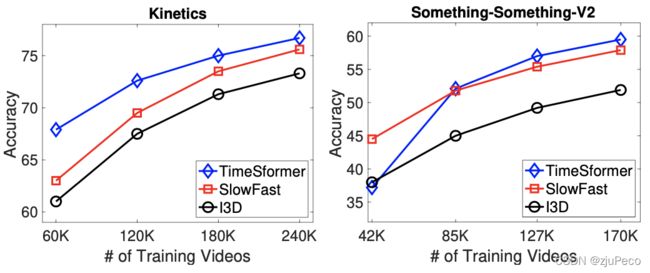
3.5 不同的数据量

不同模型在更大的数据量上，都有更好的表现，但是SSv2上，TimeSformer需要更多的数据才能学习到时间维度的重要特征。

图3-3 不同的数据量对比

3.6 position embedding的影响

position embedding对模型也有着很大的影响，在不太关注时间维度的K400上，没有time维度的position embedding也有不错的表现，但是类别识别依赖于时间维度特征的SSv2就既要space的embedding，又要time的embedding了。

position embedding在时间和空间维度都很重要。

表3-7 不同的position embedding效果对比表

3.7 长输入时长

作者对比了不同输入时长下，SlowFast和TimeSformer的效果，TimeSformer明显更适用于处理较长的视频。

表3-8 长输入时长效果对比表

对于表中的Single Clip Coverage和Test Clips，我的理解是一段视频很长，当输入为8帧时，这8帧大概涵盖了视频8.5s的内容，于是要切不相互覆盖的48个8.5s，分别过模型，并取平均。其他的也是同样的道理。

3.8 不同的transformer

作者也使用了更大和更小的vision transformer，发现更小的tranformer准确率会掉5%，更大的transfomer准确率会掉1%。作者推测更大的效果变差是因为数据集不够大。

3.9 不同的patch size

作者对比了16和32的patch size，发现16的patch size比32的patch size要好3%。但这其实和输入的尺寸也有关，这里还可以再坐下不同分辨率下不同patch size的表现。

3.10 attention的顺序

因为使用的是divided attention，所有就有time先，还是space先，还是并行的顺序问题。作者发现，time先的方式，效果要略好一点。

这的确会有些影响，举个不恰当的例子，比如往可乐瓶子里倒水，先倒热水，再倒冷水，瓶子就会经历高温，会在高温时萎缩，但是先倒冷水，再倒热水就不会经历高温了。

参考资料

[1] Is Space-Time Attention All You Need for Video Understanding?
[2] https://github.com/facebookresearch/TimeSformer