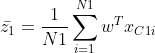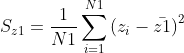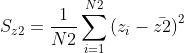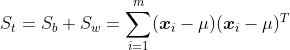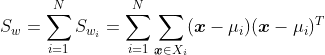线性判别分析(LDA)详解
入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。
目录
一、LDA简介
二、数学原理（以二分类为例子）
1、设定
2、每一类的均值和方差
3、目标函数
4、目标函数的求解
5、最终的实践所求
三、多分类LDA
四、LDA用途与优缺点
1、用途
2、优点
3、缺点
五、LDA的python应用
1、调用函数LinearDiscriminantAnalysis
2、常用参数意义
3、常用返回值
4、利用LDA进行二分类实例
一、LDA简介
LDA（线性判别分析）是一个经典的二分类算法。
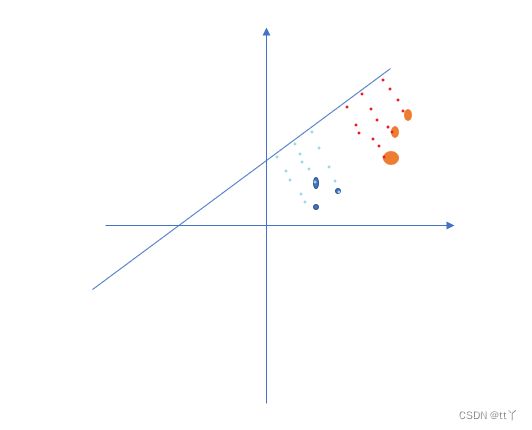
主要思想：以一种基于降维的方式将所有的样本映射到一维坐标轴上，然后设定一个阈值，将样本进行区分
如下图所示，把红蓝两类的点投影在了一条直线（向量a）上，即二维变一维（本来一个点要用(x,y)来表示，投影到直线后就用一个维度来描述）。
二、数学原理（以二分类为例子）
1、设定
首先我们假设整个样本空间分为两个类别，分别是1、-1；N1、N2分别代表1，-1类别样本的个数；样本为X。
那么有：
；
设定z为映射后的坐标（即投影后的坐标）
2、每一类的均值和方差
将样本数据X向w向量（设定w的模长为1）做投影，则有：
接下来求出映射后的均值和方差（用来衡量样本的类间距离和类内距离）
均值：
；
方差：
；
3、目标函数
想要得到好的分类模型，即要求类内间距小，类间间距大。即：
类内间距小：
；两个类的方差越小，说明样本越密集
类间间距大：
；用两个类的均值的距离说明两个类之间的距离
根据这样的思路构建目标函数：
J(w)越大越好，即我们要求的是：
4、目标函数的求解
化简目标函数：（将w向量与原数据的运算分隔开）
令类间散度矩阵：
；类内散度矩阵：
，则有：
方法一：
为了解决
化简得到：
又因为
，
，
都是标量，w前面我们已经约定它的模长为1，所以我们不关心它的长度，只关心他的方向，所以把标量都摘掉，得：
方法二：
J(w)的分子分母都是关于w的二次项，因此J(w)的解与w的长度无关，只与它的方向有关。所以这里为例简单处理也可以令
，故求
，利用拉格朗日乘子法可得：
又因为
方向恒为
，所以令
，因此有
5、最终的实践所求
为得到数值解的稳定性，通常对
进行奇异值分解（
），再由
得到
。
三、多分类LDA
假定存在N个类，且第i类示例数为
。
全局散度矩阵：
，其中
是所有样本的均值向量。
类内散度矩阵：
类间散度矩阵：
然后与上面的二分类类似：目标函数为：
类似可得：
所以W的解为
的特征向量组成的矩阵。
四、LDA用途与优缺点
1、用途
LDA既可以用来降维（将W视为投影矩阵），又可以用来分类，但主要还是用于降维。
2、优点
与另一个降维算法PCA对比
（1）在降维过程中可以使用类别的先验知识经验，而PCA（无监督学习）无法使用类别先验知识
（2）LDA样本分类依赖的是均值而不是方差，比PCA算法更优
3、缺点
（1）LDA不适合对非高斯分布的样本降维
（2）LDA降维最多降到类别数N-1的维数，如果我们降维的维度大于N-1，则不能使用LDA
（3）LDA可能会过度拟合数据
五、LDA的python应用
1、调用函数LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis2、常用参数意义
（1）solver：字符串类型，指定求解最优化问题的算法
'svd'：奇异值分解。对于有大规模特征的数据，推荐用这种算法
'lsqr'：最小平方差，可以结合skrinkage参数
'eigen' ：特征分解算法，可以结合shrinkage参数
（2）skrinkage：取值：字符串‘auto’或者浮点数或者None。
该参数通常在训练样本数量小于特征数量的场合下使用。
‘auto’：自动决定shrinkage参数的大小
None：不使用shrinkage参数
浮点数（位于0~1之间）：自己指定的shrinkage参数
（3）n_components：（整数类型）指定了数组降维后的维度（该值必须小于n_classes-1）
（4）priors：一个数组，数组中的元素依次指定了每个类别的先验概率。如果为None，则认为每个类的先验概率都是等可能的
3、常用返回值
coef_：权重向量
intercept：b值
covariance_：一个数组，依次给出了每个类别的协方差矩阵
means_：一个数组，依次给出了每个类别的均值向量
xbar_：给出了整体样本的均值向量
4、利用LDA进行二分类实例
来个简单的小栗子
我们使用sklearn里的乳腺癌数据集
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()然后对数据进行一个处理，让我们看起来舒服点，计算机处理也舒服点
data=cancer["data"]
col = cancer['feature_names']
x = pd.DataFrame(data,columns=col)#就是那些个特征
target = cancer.target.astype(int)
y = pd.DataFrame(target,columns=['target'])#对应特征组合下的类别标签训练集测试集分分类
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1)直接进入训练
clf = LinearDiscriminantAnalysis(n_components=1)
model=clf.fit(x_train,y_train)训练出来的模型对test集进行一个预测
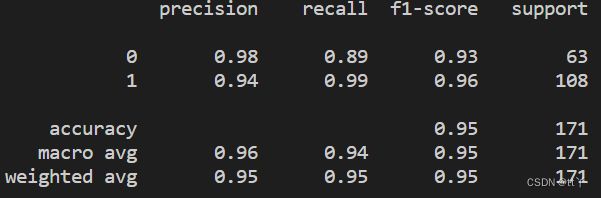
y_pred = model.predict(x_test)
print(classification_report(y_test, y_pred))完整代码
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
cancer = load_breast_cancer()
data=cancer["data"]
col = cancer['feature_names']
x = pd.DataFrame(data,columns=col)
target = cancer.target.astype(int)
y = pd.DataFrame(target,columns=['target'])
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1)
clf = LinearDiscriminantAnalysis(n_components=1)
model=clf.fit(x_train,y_train)
y_pred = model.predict(x_test)
print(classification_report(y_test, y_pred))结果
欢迎大家在评论区批评指正，谢谢~