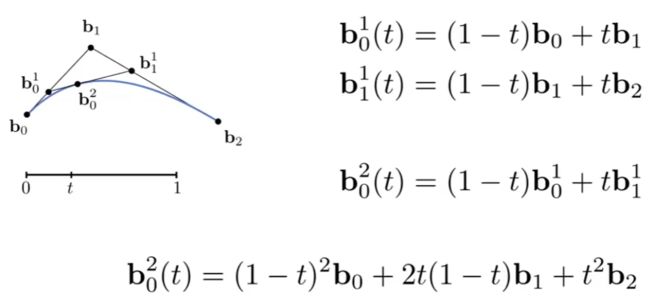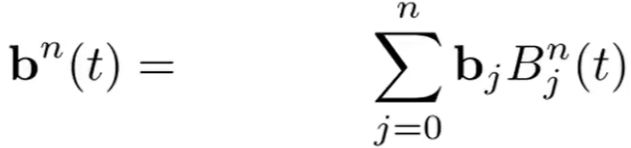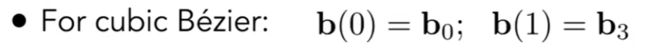Games101-课程11笔记

目录

第十一节课 : 曲线和曲面

点云

多边形面:

Wavefront Object File Format(.Obj文件) :

曲线:

贝塞尔曲线

德卡斯特里奥算法算出贝塞尔曲线

计算贝塞尔曲线的代数公式

贝塞尔多项式 

伯思斯坦多项式

贝塞尔曲线的性质

B-splines (B样条)

贝塞尔曲面

 得到贝塞尔曲面过程

 贝塞尔曲面计算图

 具体做法

---

第十一节课 : 曲线和曲面

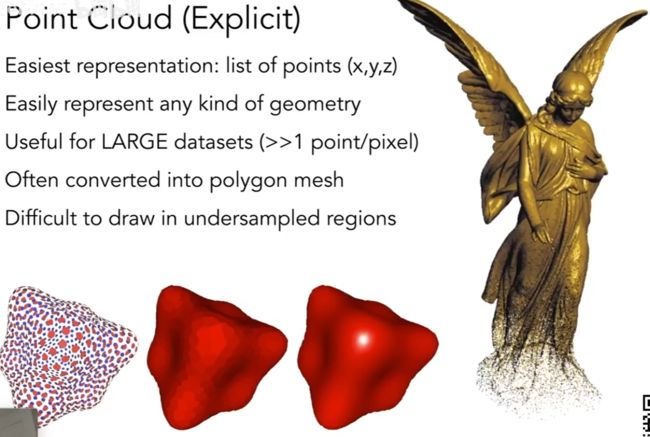
点云 (点的集合)

① 可表示任何一个几何

② 扫描得出一堆点云, 如何通过点云得出它们所构成的多角形.

 

多边形面(Polygon Mesh) :

① 易于做处理/模拟,附加采样

② 更多链接数据结构

③ 在图形学中,得到最广泛的显示表示

 

Wavefront Object File Format(.Obj文件) :

所包含内容有:

V : 顶点坐标

Vt : 纹理坐标

Vn : 法线向量

f 5/1/1 :表示取第5个顶点坐标v5, 第1个纹理坐标vt1, 第1个法线向量vn1

f 5/1/1  1/2/1  4/3/1 :表示v5, v1, v4三个顶点坐标连成一个三角形, 一一对应的纹理坐标为vt1, vt2, vt3, 法线为vn1.

 

曲线(Curves) :

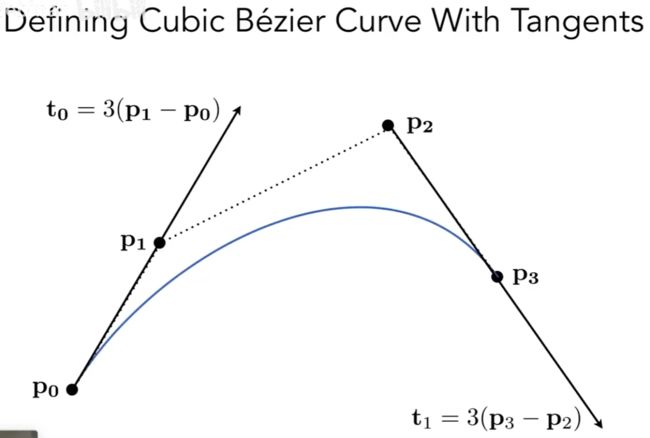
贝塞尔曲线(Bezier Curves):

① 必须经过起始点p0,p3

② 沿着p0p1方向走, 往p2p3方向出去, 必须是沿着切线方向来和走.

四个控制点

 

德卡斯特里奥算法(de casteljau algorithm)算出贝塞尔曲线 :

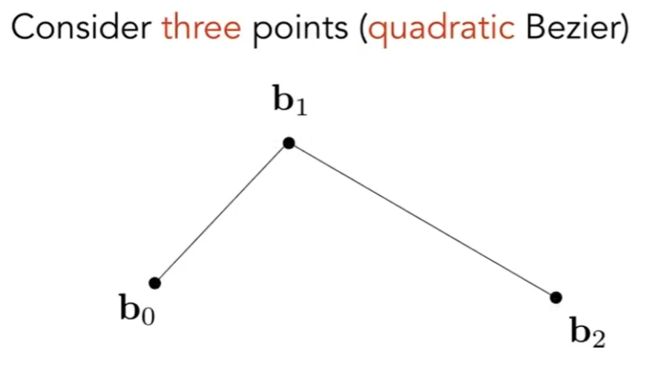
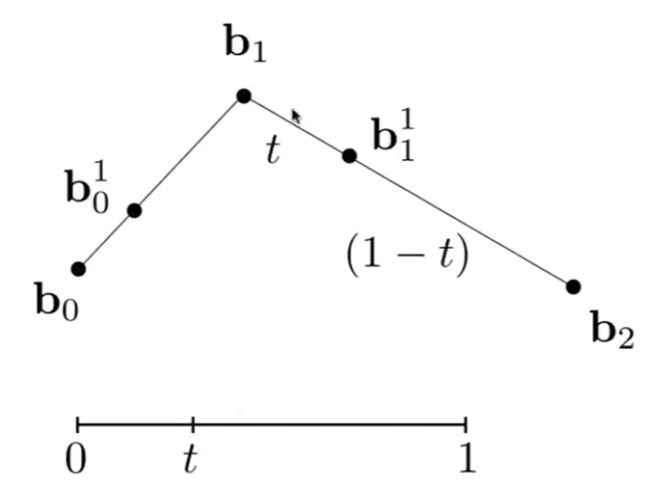
三个点组成 (下面曲线名字为二阶贝塞尔曲线quadratic Bezier)

 

定义曲线起点时间t为0, 终点为1

所以画出这条曲线, 相当于给出在时间0~1, 点在平面上的位置

显示表示几何(拥有参数t)

算法过程 :

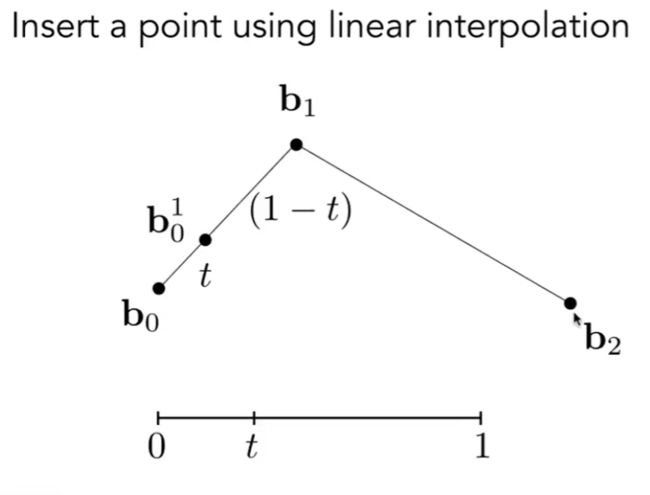
① 假设现在参数时间t =1/3

② 找出b0到b1线段上1/3位置b10

 ③ 同样道理, 找出b1和b2线段上1/3的位置b11

 

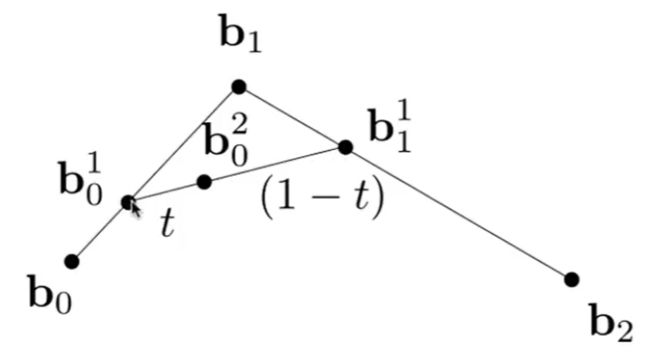
④ 把b10和b11两个点连起来, 找出b10和b11线段上1/3的位置b20

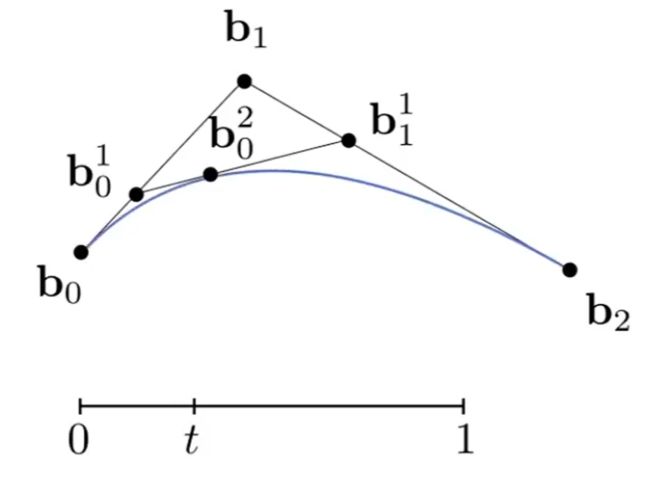
⑤ 这个b20就是在时间t=1/3时, 位于二阶贝塞尔曲线上的点.

⑥ 只要用以上算法, 给t设足够多的值, 枚举出足够多的点, 就可以画出二阶贝塞尔曲线

 

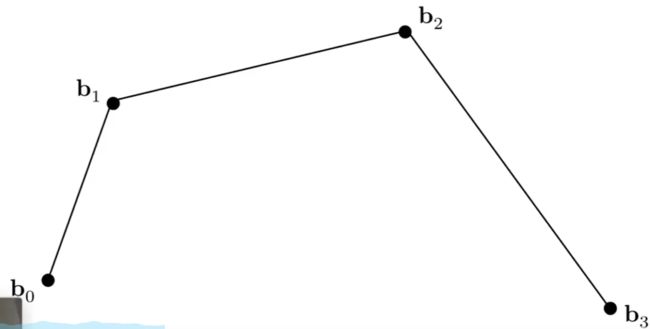
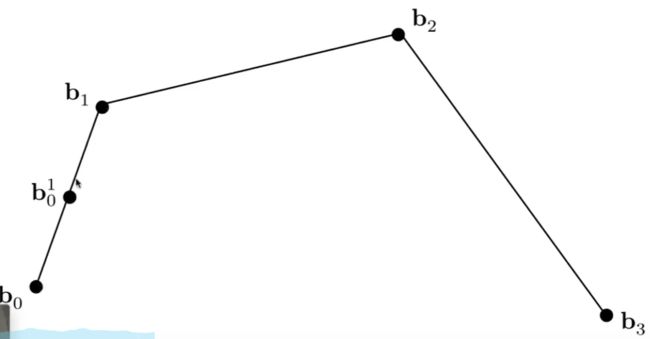
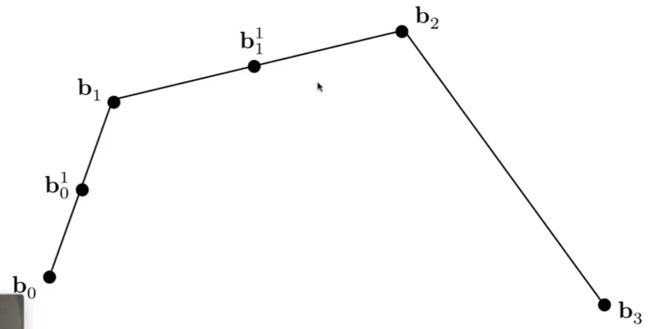
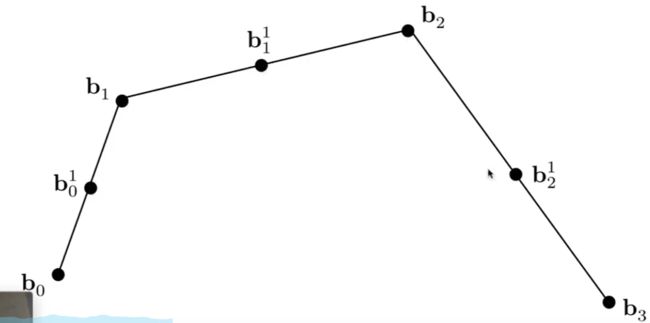
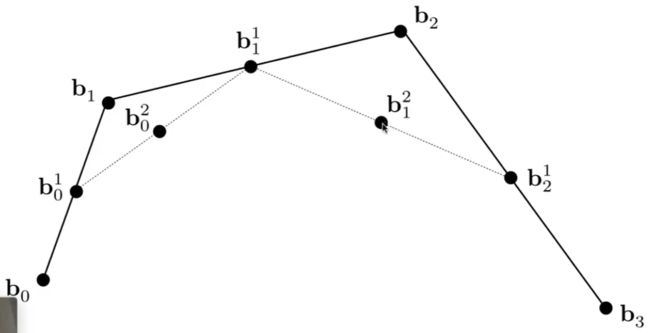
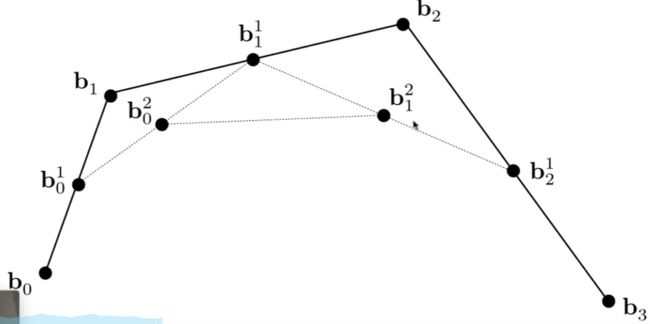
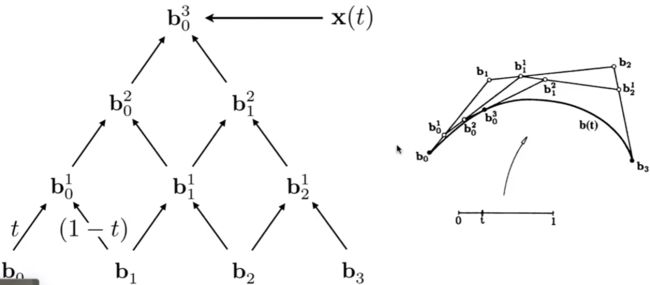
四个点组成的三阶贝塞尔曲线 :

流程图 :

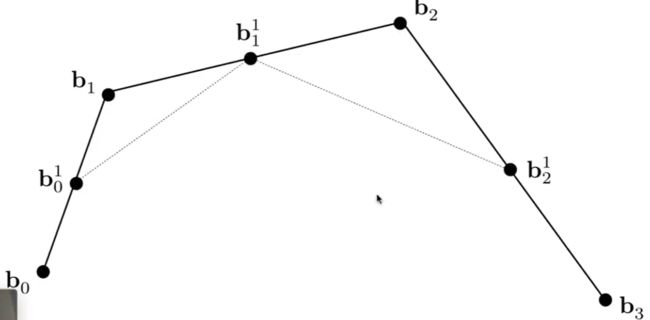
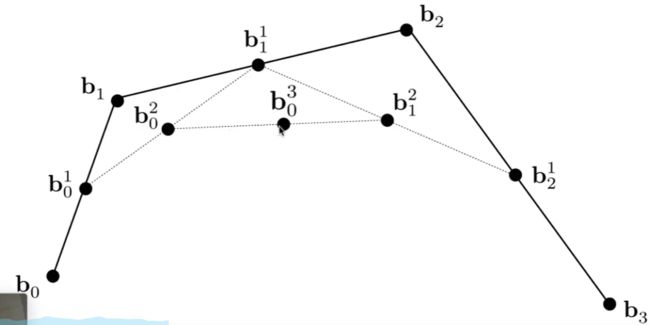
这里假设t =0.5

 

 

 

 

 

 

 

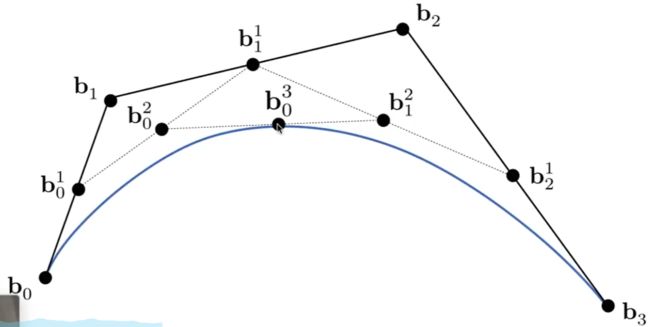
最后就找到了在时间t=0.5下, 位于三阶贝塞尔曲线的点.

枚举出更多的点, 就能得出三阶贝塞尔曲线

 

计算贝塞尔曲线的代数公式

每一个向右的箭头都是乘以t

每一个向左的箭头是乘以（1-t）

每两个点做一个线性插值, 得出一个点.

 

将过程显示写出来 :

当t = 0, 就是b0位置

 

总结 :

总共有n个控制点, 可以得到n-1阶的贝塞尔曲线.

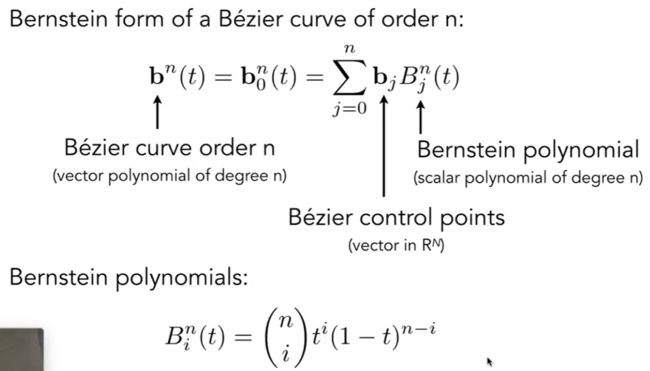
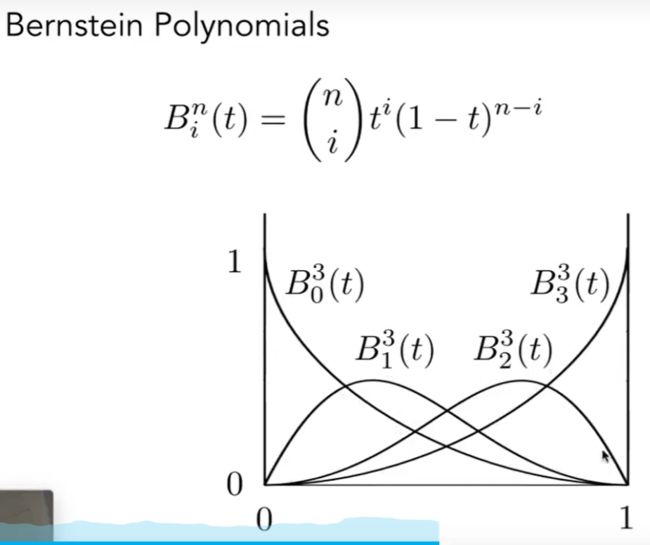
贝塞尔多项式 :

贝塞尔曲线都是之前给定点的线性组合, 它们的系数是伯思斯坦多项式(Bernstein polynomial)

 

将上述公式简化 :

n(左边式子)表示多少阶, 控制点为0阶, 每插值操作一次得到的所有点升1阶.

j 表示第几个控制点.

 举例四个控制点, 将贝塞尔多项式展开

 伯思斯坦多项式(Bernstein polynomial) :

 

贝塞尔曲线的性质 :

下面以三个控制点组成的二阶贝塞尔曲线为例

① t = 0时,一定在起点;         t = 1时, 一定在终点.

② 这只是四个控制点的公式 :(如果不是四个,那么系数不一定是3)

b’(0) :起始的切线方向         b’(1) :终点的切线方向

 ③ 只在仿射变换下才能保证与原来的贝塞尔曲线一致,其它变换不行(投影等等): 通过变换控制点来变换曲线

 

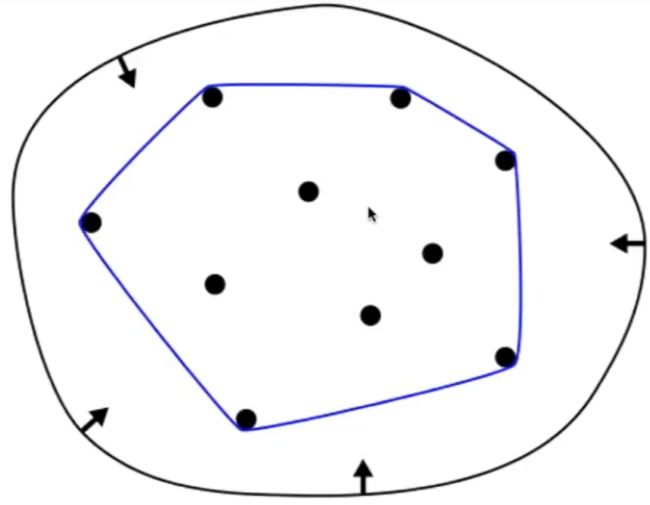
④ 凸包性质

画出的贝塞尔曲线, 必须在由控制点组成的凸包内.

 

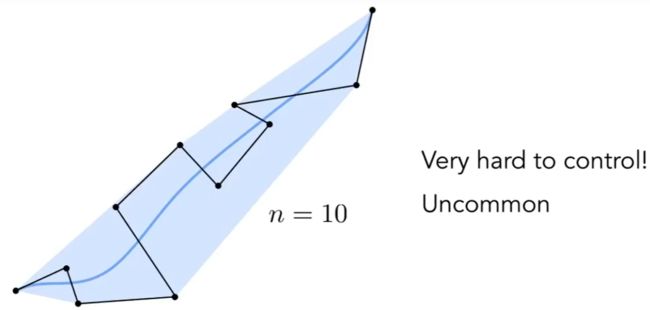
⑤ 高阶贝塞尔曲线(多个控制点组成) :

缺点 :不利于控制它的走向

 

⑥ 为了解决难控制问题 :

提出了分段三次贝塞尔曲线

(通过四个控制点形成的低阶贝塞尔曲线, 将它们连在一起得到更长的高阶贝塞尔曲线).

 

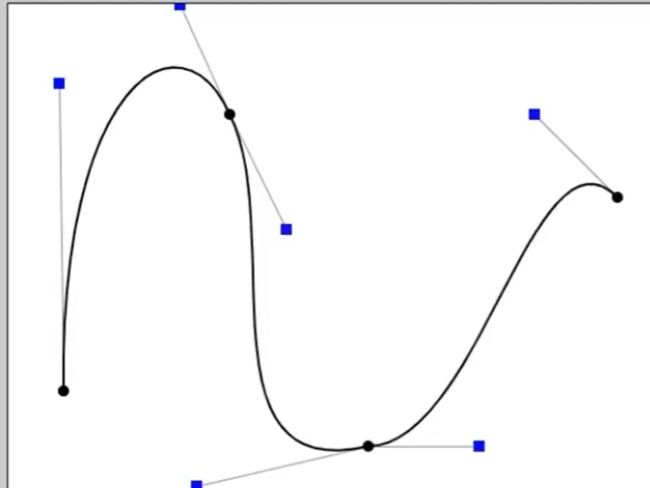
⑦ 如何使终点光滑(往切线方向)

答 :相关的两个控制点离终点距离一样, 且共线.

例子看如下 :(从左往右)第3,4个控制点

 

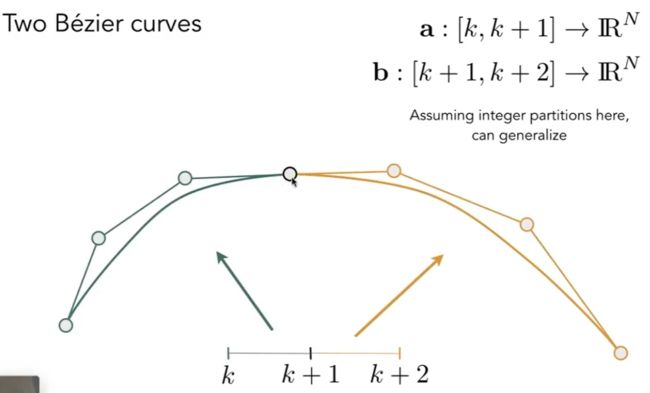
两条贝塞尔曲线 :

 

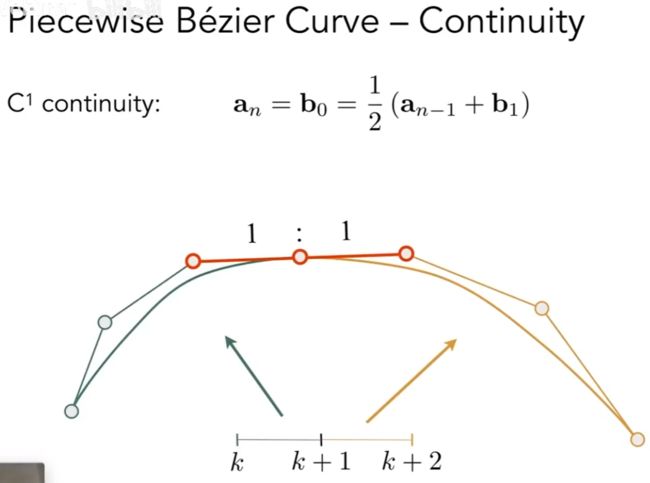
不同的两条贝塞尔曲线的连续定义 :

① 曲线的终点是另一条曲线的起点

② 切线连续,向量(a(n)-a(n-1))与(b(1)-b(0))长度一样, 方向一样

 

B-splines (B样条)

在本节课就不阐述, 需要深入学习进入下方网站.

 

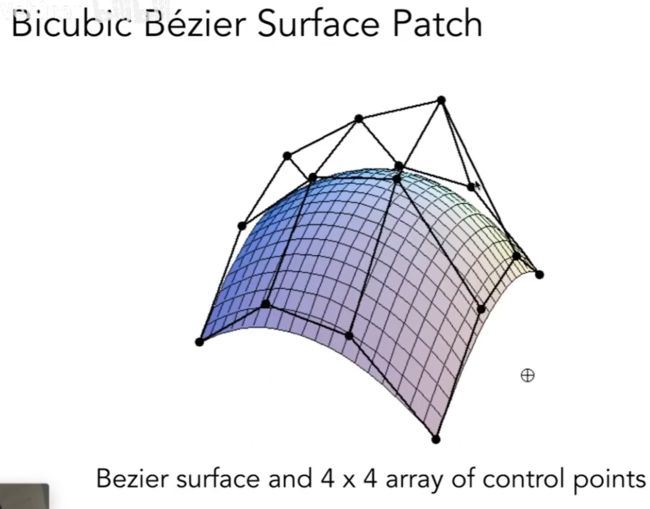
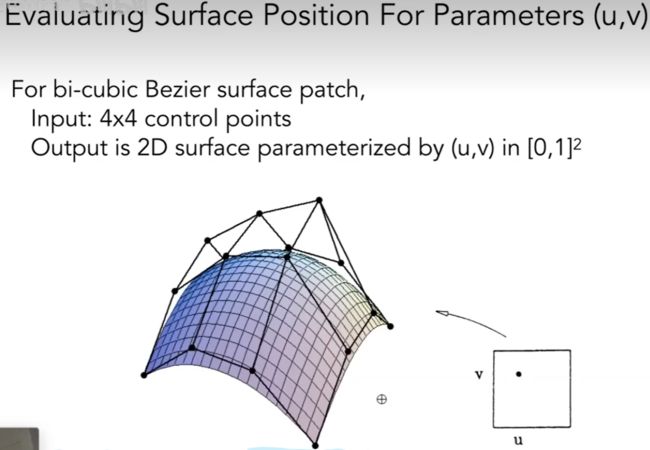
贝塞尔曲面

例子:

 用4*4的控制点形成一个曲面 :

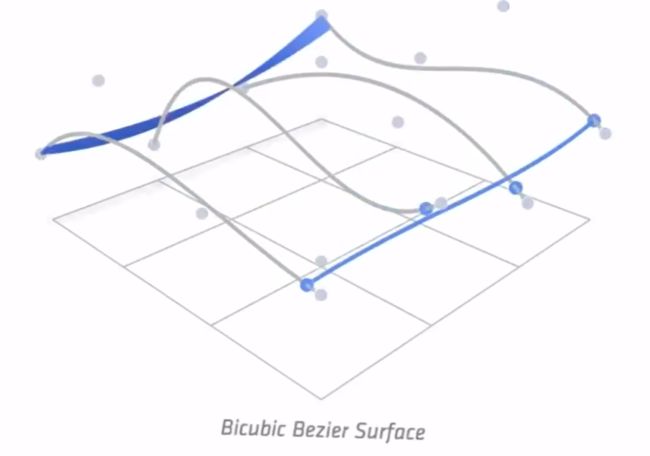
 得到贝塞尔曲面过程 :

  

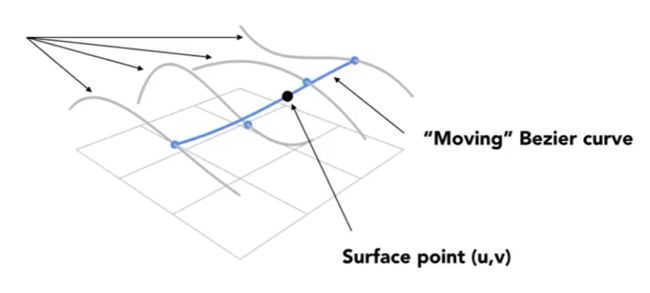
 贝塞尔曲面计算图 :

 

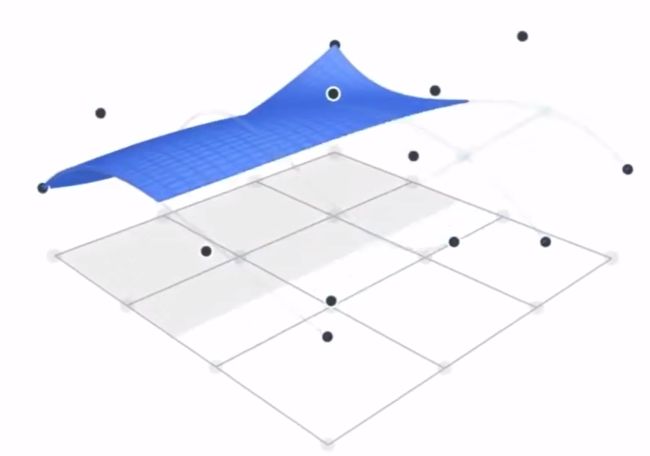
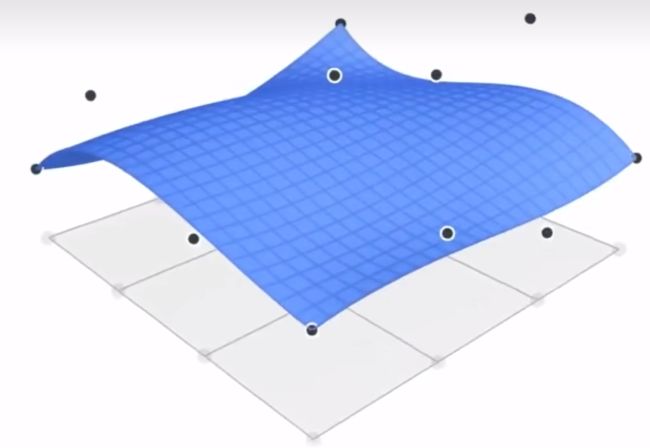
具体做法 :

需要 :

① 4*4的控制点

② 一个2D的(u , v)坐标, 类似于纵向的t1 (求在纵向上每条贝塞尔曲线在 t1时刻的点(蓝线), 下图中的四个点), 横向的t2(求横向上t2时的点, 下图中四个点连成的一条横向的线).