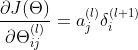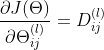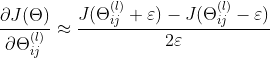BP神经网络
为什么要使用神经网络?
虽然对于分类问题,可以运用Logistic回归,但是对于一些过于复杂的非线性训练集合,既分类问题,Logistic回归的决策边界可能会过于复杂,而且可能会导致过拟合的问题,如下图所示:
对于这个有两个特征变量![]() 和
和![]() 的分类问题,可以用包含许多非线性项的Logistic函数,既假设函数来拟合数据集
的分类问题,可以用包含许多非线性项的Logistic函数,既假设函数来拟合数据集
当多项式足够多时,或许可以划分决策边界, 把正负样本给区分开。
但是许多分类问题中可能特征远不止两项,假设有100个特征变量
这样光是二次项就有5151种可能,将![]()
故二次项的数量呈![]() 的复杂度递增,而三次项的数目就会更多,呈
的复杂度递增,而三次项的数目就会更多,呈![]() 的复杂度递增,故即使只是包含全部的二次项,Logistic回归也并不是一个很好的选择,最后得出的结果可能也会过拟合。
的复杂度递增,故即使只是包含全部的二次项,Logistic回归也并不是一个很好的选择,最后得出的结果可能也会过拟合。
所以,当特征个数![]() 很大时,将这些高阶多项式项数包括到特征里,会使特征空间急剧膨胀,而对于许多实际的机器学习问题,特征变量的个数
很大时,将这些高阶多项式项数包括到特征里,会使特征空间急剧膨胀,而对于许多实际的机器学习问题,特征变量的个数![]() 是很大的,如下例所示:
是很大的,如下例所示:
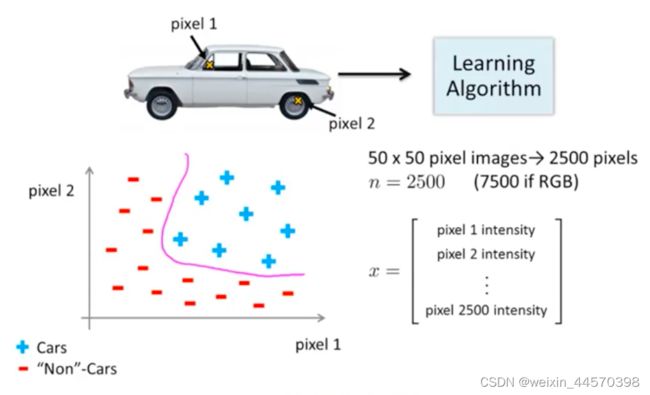
要辨别图像是否为一辆汽车,以其中的两个像素点作为输入特征可以简单地划分是正负样本,但一张图片可能包含许多像素点,假设图片都是![]() 像素,一张图片一共有2500个像素点。因此,特征向量的元素个数
像素,一张图片一共有2500个像素点。因此,特征向量的元素个数![]() 就是2500,如果我们想通过包含所有二次项特征的假设函数来学习得到的非线性假设,那总共就会包含约
就是2500,如果我们想通过包含所有二次项特征的假设函数来学习得到的非线性假设,那总共就会包含约![]() 个特征,特征空间过大严重影响Logistic回归算法的效率。
个特征,特征空间过大严重影响Logistic回归算法的效率。
所以,用包含二次项和三次项的简单Logistic回归来学习当特征个数![]() 很大时的非线性假设并不是一个很好的方法。
很大时的非线性假设并不是一个很好的方法。
神经网络模型
下图是一个简单的只包含单个神经元的神经网络模型,黄色圆圈表示神经元细胞体,用于处理接收到的信息,既一个逻辑单元,通过树突或者输入通道输入特征变量![]() ,
,![]() 和
和![]() ,最后通过轴突输出计算结果,既假设函数,在神经网络里也可以称为激活函数(activation function)。
,最后通过轴突输出计算结果,既假设函数,在神经网络里也可以称为激活函数(activation function)。
![]()
其中特征向量![]() 和参数向量
和参数向量![]() 为
为
在绘制神经网络模型时,一般只绘制输入特征,而不会加上![]() ,因为
,因为![]() 。当在有必要的时候加上
。当在有必要的时候加上![]() 时,把
时,把![]() 称为偏置单元(bias unit)。
称为偏置单元(bias unit)。
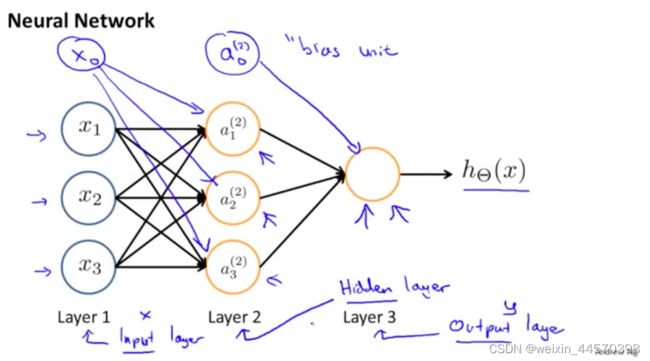
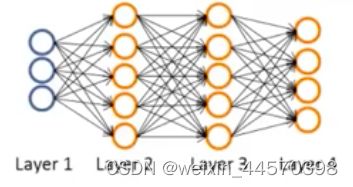
但神经网络其实是一组神经元连接在一起的集合,如下图所示
把用于输入特征变量 的第一层称为输入层(input layer),最后一层用于输出假设函数的称为输出层(output layer),而中间用于处理数据的神经元都被称为隐藏层(hidden layer)。除了输出层之外的每一层都可以加入偏置单元,且都为1。
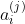 表示第
表示第 层第
层第 个激活项
个激活项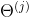 是权重矩阵,既参数矩阵,它控制着从第
是权重矩阵,既参数矩阵,它控制着从第 层到第
层到第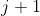 层的映射,因为
层的映射,因为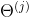 是矩阵所以要大写
是矩阵所以要大写
每个激活项的表达式如下
输出单元的表达如下
因此![]() 是一个
是一个![]() 的矩阵,
的矩阵,![]() ,它控制着第1层输入层到第2层隐藏层的映射
,它控制着第1层输入层到第2层隐藏层的映射
而![]() 是一个
是一个![]() 的矩阵,
的矩阵,![]() , 它控制着第2层隐藏层到第3层输出层的映射
, 它控制着第2层隐藏层到第3层输出层的映射
由此可知![]() ,
,![]() 是第
是第![]() 层激活项加上该层的偏置项的个数,
层激活项加上该层的偏置项的个数,![]() 是第
是第![]() 层激活项的个数。
层激活项的个数。
1、前向传播算法
对神经网络模型进行向量化,将每个激活项进行化简
![]()
那么激活项![]() 为
为
同理可得![]() ,
,![]() 和
和![]() ,
,![]() ,那么
,那么
而特征变量![]() 为
为
因此![]() 可以简化成权重矩阵
可以简化成权重矩阵![]() 和添加进偏置项
和添加进偏置项![]() 的特征向量
的特征向量![]() 相乘
相乘
故![]() 为
为
![]()
把第1层输入层作为第1层激活层![]() ,既
,既
![]()
以此类推,将偏置项![]() 加入
加入![]() ,可得输出层
,可得输出层![]() 为
为
![]()
这就是前向传播算法的向量表示,我自己把它理解为,最后输出层得到的就是神经网络的模型,既假设函数。
这是二元分类的例子,而在多元分类(multi-class classification)问题中,最后输出层输出的是一个向量,![]() 元分类问题就是
元分类问题就是![]() 维向量。如下图所示,要分辨出图像的类别,是轿车,行人,摩托车还是卡车,则是4元分类问题,输出的就是4维向量。
维向量。如下图所示,要分辨出图像的类别,是轿车,行人,摩托车还是卡车,则是4元分类问题,输出的就是4维向量。
![]()
![]()
当该图像是行人时,则目标变量![]() 和假设函数
和假设函数![]() 分别为
分别为
当该图像轿车是时,则目标变量![]() 和假设函数
和假设函数![]() 分别为
分别为
以此类推。
2、激活函数的选择
如果要解决回归问题,毫无疑问选择线性函数;如果我们要解决二元分类问题,隐藏层选择ReLU函数,输出层选择sigmoid函数;如果要解决多元分类问题,隐藏层依然选择ReLU函数,但是输出层选择softmax函数。选择sigmoid函数也可行,但是需要同时修改代价函数。
如果都选择用线性的激活函数,从输入层开始
![]()
![]()
![]()
![]()
![]()
因此最后输出层输出的值依旧是线性的,就等同于线性回归。
3、代价函数
假设有如图所示神经网络
训练集有![]() 个训练样本
个训练样本
![]()
-
 表示这个神经网络的总层数
表示这个神经网络的总层数  表示第
表示第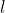 层神经元的数量,既激活项的数量。这个数量不包括偏置项
层神经元的数量,既激活项的数量。这个数量不包括偏置项
神经网络的代价函数是Logistic回归代价函数的一般形式,因为Logistic回归只有一个目标变量![]() ,所以也只会有一个逻辑回归输出单元
,所以也只会有一个逻辑回归输出单元![]() ,而对于神经网络来说可能会有一个
,而对于神经网络来说可能会有一个![]() 维的目标向量
维的目标向量![]() ,所以输出的也是一个
,所以输出的也是一个![]() 维向量
维向量![]()
![]() ,
,![]()
那么![]() 就表示输出层
就表示输出层![]() 维向量中的第
维向量中的第![]() 个输出单元,因此输出层的激活函数为sigmoid函数的神经网络的代价函数
个输出单元,因此输出层的激活函数为sigmoid函数的神经网络的代价函数![]() 为
为
输出层的激活函数为softmax函数的神经网络的代价函数![]() 为
为
4、反向传播算法
在得到神经网络模型的代价函数后,需要找到参数![]() 使得代价函数最小,既求出代价函数的最小值
使得代价函数最小,既求出代价函数的最小值![]() ,无论是利用梯度下降法还是别的高级算法,要求出
,无论是利用梯度下降法还是别的高级算法,要求出![]() ,都需要计算每个参数的偏导数,既求出
,都需要计算每个参数的偏导数,既求出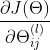 。
。
从输出层开始,从后往前开始求导。输出层为
而![]() 为
为
对![]() 的第一行
的第一行![]() 开始求导,当选用sigmoid函数作为输出层的激活函数时,除了
开始求导,当选用sigmoid函数作为输出层的激活函数时,除了![]() ,其余输出项对
,其余输出项对![]() 求偏导都为0,因此
求偏导都为0,因此
当选用softmax函数作为输出层的激活函数时,
除了第![]() ,其余输出项全部为0,因此
,其余输出项全部为0,因此
接下来对![]() 进行求导
进行求导
其中由之前对![]() 求导可知,
求导可知,
或者
同样先对![]() 求导,而除了
求导,而除了![]() ,其余激活项对
,其余激活项对![]() 的偏导数也都为0,因此
的偏导数也都为0,因此
以此类推
然后对![]() 进行求导
进行求导
其中
先以一个训练样本![]() 为例,利用前向传播算法得出输出层输出向量,既假设函数
为例,利用前向传播算法得出输出层输出向量,既假设函数![]() 的向量
的向量
![]()
![]()
![]()
![]()
![]()
![]()
![]()
接下来为了计算偏导项,将利用反向传播算法(Backpropagation),反向传播算法就是对每一个激活项计算![]() ,
,![]() 代表第
代表第![]() 层第
层第![]() 项的误差,从后往前计算。从输出层开始
项的误差,从后往前计算。从输出层开始
![]()
因此转化为向量形式为
![]()
而之前几层的误差项的计算方式和最后一层输出层有所区别
![]()
![]()
“![]() ”表示向量中的项两两相乘。又因为
”表示向量中的项两两相乘。又因为![]() 为
为
故![]() 可以化简为
可以化简为
![]()
而第一层![]() 为输入层也就是特征向量
为输入层也就是特征向量![]() ,不存在误差,也就没有
,不存在误差,也就没有![]() 。
。
所以误差项的一般形式为
![]()
![]()
向量化后为
对![]() 个训练样本重复以上操作,把偏导矩阵记作
个训练样本重复以上操作,把偏导矩阵记作![]() ,并对所有训练样本所对应参数的偏导矩阵求和
,并对所有训练样本所对应参数的偏导矩阵求和
![]()
最后分两种情况选择是否对正则项求偏导
由此可知所有参数的偏导数为
5、梯度检测
由偏导数的定义可知
为了检测后向传播算法是否正常运行,对![]() 以及偏导数
以及偏导数![]() 的计算是否有误差,如果
的计算是否有误差,如果
则说明后向传播算法正常运行,对偏导数的计算误差不大,![]() 一般选择一个很小的值在
一般选择一个很小的值在![]() 左右。
左右。
但是注意,在用神经网络训练数据时,要把梯度检测给关掉,以为梯度检测的计算量非常大,计算偏导数会非常慢,而反向传播算法的速度就很快,所以为了提高模型的效率,在训练神经网络时,要把梯度检测给关掉。
6、随机初始化
在利用梯度下降法或其他高级算法计算![]() 是,会先初始化参数的值,一般全部设置为0,但是在神经网络中,因为
是,会先初始化参数的值,一般全部设置为0,但是在神经网络中,因为
![]()
如果把初始的参数全部设置为0,既![]() 那么
那么
![]()
因为每层每个激活项的值都相等,每层每个误差项![]() 也相等。那么就会导致输入的特征冗余,且下降每次每个参数
也相等。那么就会导致输入的特征冗余,且下降每次每个参数![]() 都下降相同的程度。
都下降相同的程度。
为了解决这个问题,在神经网络中对参数进行初始化时,要使用随机初始化的思想,对参数![]() 在随机范围
在随机范围![]() 初始化,既
初始化,既
![]()
这里的![]() 和梯度检测
和梯度检测![]() 是不同的
是不同的![]() ,注意区分。
,注意区分。

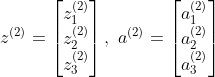
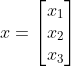
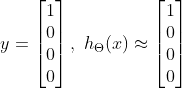
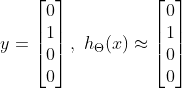
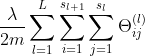
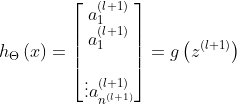
![\frac{\partial J\left ( \Theta \right )}{\partial z^{(l+1)}}=\frac{1}{m}\left [ \sum_{i = 1}^{m} \left (h_{\Theta } \left ( x^{(i)} \right ) - y^{(i)} \right ) \right]](http://img.e-com-net.com/image/info8/81eb641b58844a4399b9ea19612dfe1a.gif)