动手学深度学习v2笔记-Day9-卷积神经网络
动手学深度学习v2
Day 9
原书第六章笔记,会不断修改补充内容,如有任何错误,欢迎指出
0x00 预备知识
建议在这章的学习之前先看完下面三个视频
什么是卷积神经网络CNN?【知多少】
大白话讲解卷积神经网络工作原理
从“卷积”、到“图像卷积操作”、再到“卷积神经网络”,“卷积”意义的3次改变
0x01 平移不变性&&局部性
1.平移不变性
假设我想在一张图片中找到某个物体,那么我的方法一定跟这个物体在图片中的哪个位置无关,否则我解决的就是在某个或者某种特定位置找到这个物体的问题。
之前提到的多层感知机结构的输入一直是一个向量形式,即使我们对图片进行预测的时候,也是将二维图片拉成一维向量进行输入的,但是这样丢失了图片中的空间信息,每个像素点之间的关联也变少了。
那么我们根据平移不变性需要对原来的全连接层进行一定的改动以实现二维图片的输入。
-
首先将全连接层的输入变成矩阵
由
h j = ∑ j w i , j x j h_j = \sum_{j}w_{i,j}x_j hj=j∑wi,jxj
变成
h i , j = ∑ i , j w i , j , k , l x k , l h_{i,j} = \sum_{i,j}w_{i,j,k,l}x_{k,l} hi,j=i,j∑wi,j,k,lxk,l
这样增加了长宽,和长宽分别的权重 -
此时对w进行重新索引如下
v i , j , a , b = w i , j , i + a , j + b v_{i,j,a,b} = w_{i,j,i+a,j+b} vi,j,a,b=wi,j,i+a,j+b -
那么之前的式子变成
h i , j = ∑ i , j v i , j , a , b x i + a , j + b h_{i,j} = \sum_{i,j}v_{i,j,a,b}x_{i+a,j+b} hi,j=i,j∑vi,j,a,bxi+a,j+b
这里目的是构造k,l和i,j的关系
根据平移不变性,我们认为任何输入都不会影响我们识别特征的这个东西,但是目前看上式,输入的ij会影响这个v的值(这里将v理解成卷积核)
- 解决方案
将
v i , j , a , b = v a , b v_{i,j,a,b} = v_{a,b} vi,j,a,b=va,b
带入得出
h i , j = ∑ a , b v a , b x i + a , j + b h_{i,j} = \sum_{a,b}v_{a,b}x_{i+a,j+b} hi,j=a,b∑va,bxi+a,j+b
上式即为二维卷积交叉相关
2.局部性
找某个物体的过程中,我不需要看到太远的距离,只需要看到某一部分就可以。
那么到卷积神经网络中,我们认为在评估最终的输出 h i , j h_{i,j} hi,j 时,不需要关注远离 x i , j x_{i,j} xi,j 的像素点,只看他附近的就可以了,于是
在上式中给一个阈值 Δ \Delta Δ ,当 ∣ a ∣ , ∣ b ∣ > Δ |a|,|b| > \Delta ∣a∣,∣b∣>Δ 时, v a , b = 0 v_{a,b}=0 va,b=0
- 于是最终
h i , j = ∑ a = − Δ Δ ∑ b = − Δ Δ v a , b x i + a , j + b h_{i,j} = \sum_{a=-\Delta}^\Delta\sum_{b=-\Delta}^{\Delta}v_{a,b}x_{i+a,j+b} hi,j=a=−Δ∑Δb=−Δ∑Δva,bxi+a,j+b
3.总结
上述描述了对全连接进行如何变换可以得到卷积层(使用平移不变性&局部性)
交叉相关||互相关 (cross-correlation)
和卷积操作差两个负号 v a , b v_{a,b} va,b 和 v − a , − b v_{-a,-b} v−a,−b 的区别,由于对称性,在实际应用中没有太大区别
在图像处理中,卷积层的好处是大量的减少了参数(比全连接层)
0x02 卷积层
1.二维交叉相关运算
首先选择一个核矩阵(卷积核)
使用这个卷积核来滑动窗口进行卷积运算(哈达玛积)(对应位置元素相乘,最终求和)
输出一个运算后的特征矩阵
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): # 实现二维交叉相关操作
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum() # python语法糖,很烦,新手很难读懂
return Y
2.二维卷积层
图片的像素输入不一定都是正方形(长等于宽)所以卷积核的长宽也不一定相等
输入 X : n h ∗ n w X: n_h * n_w X:nh∗nw
卷积核 W : k h ∗ k w W: k_h * k_w W:kh∗kw
偏差 b b b
输出 Y : ( n h − k h + 1 ) ∗ ( n w − k w + 1 ) Y: (n_h-k_h+1) * (n_w-k_w+1) Y:(nh−kh+1)∗(nw−kw+1) 这里我们可以看出每次的输出都会使输入变小,这个问题我们后续讨论
在卷积层中 W , b W,b W,b 都是可学习的参数
3.简单边缘检测
- 定义一个简单输入模拟图片
X = torch.ones((6, 8))
X[:, 2:6] = 0
print(X)
- 长这样
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
- 定义一个卷积核
K = torch.tensor([[1.0, -1.0]])
- 二维交叉相关操作
Y = corr2d(X, K)
print(Y)
- 结果这样
可以看出将0,1交界处也就是我们所谓的图像中的边缘已经被我们设置的卷积核识别出来了,并且长宽也是上述计算式子应该输出的数值
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
- 输入X的转置
print(corr2d(X.t(), K))
可以看出这个卷积核无法识别到水平方向的边缘
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
4.学习卷积核
用nn来构造二维卷积层,输入输出通道都是1,有一个1*2的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)
- 训练
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2
conv2d.zero_grad()
l.sum().backward()
# 迭代卷积核
conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad # 手动梯度下降
if (i + 1) % 2 == 0:
print(f'epoch {i+1}, loss {l.sum():.5f}')
print(conv2d.weight.data.reshape(1, 2))
- 可以发现10个epoch之后已经降到非常低的水平了,而且学习的结果和(1,-1)接近
epoch 1, loss 9.82232
epoch 2, loss 4.71599
epoch 3, loss 2.37505
epoch 4, loss 1.25658
epoch 5, loss 0.69630
epoch 6, loss 0.40143
epoch 7, loss 0.23881
epoch 8, loss 0.14542
epoch 9, loss 0.09003
epoch 10, loss 0.05638
tensor([[ 1.0153, -0.9673]])
0x03 填充&&步幅
这里是控制输出大小的两个超参数
1.填充
还记得之前提到的,经过卷积核处理后,输出会变小的问题,因此有结论如下:
卷积的输出形状取决于输入形状和卷积核的形状
举个例子,我们对一个6*6的图片应用3*3的卷积核,每次长宽会减少2,那么两层之后,特征图就只剩6-2-2=2的长宽了,这对于我们想构造一个足够深的网络显然是不利的。
带填充的二维交叉相关运算
- 顾名思义,填充就是在原始图片或者特征图上进行周围填充操作
- 一般填充0
- 通常添加 p h p_h ph 行 p w p_w pw 列填充,上下左右各一半
- 输出形状变成 ( n h + p h − k h + 1 ) ∗ ( n w + p w − k w + 1 ) (n_h+p_h-k_h+1) * (n_w+p_w-k_w+1) (nh+ph−kh+1)∗(nw+pw−kw+1)
- 通常情况我们取的填充值为卷积核的长宽各减1
- 通常情况我们取卷积核的长宽均为奇数(可以在两侧各填充相等的数据量,对称性)
import torch
from torch import nn
def comp_conv2d(conv2d, X):
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
return Y.reshape(Y.shape[2:])
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1) # 3*3的卷积核
X = torch.rand(size=(8, 8)) # 输入是8*8的
print(comp_conv2d(conv2d, X).shape)
可以看出输出也是8*8的,在填充之后输入输出维度保持一致
torch.Size([8, 8])
2.步幅
在滑动窗口的时候,之前默认是每次滑动一个像素,步幅就是控制每次滑动多少个像素的超参数
水平步幅为2,垂直步幅为3
-
通常垂直步幅为 s h s_h sh 水平步幅为 s w s_w sw 时,输出形状如下
⌊ ( n h + p h − k h + s h ) / s h ⌋ ∗ ⌊ ( n w + p w − k w + s w ) / s w ⌋ \lfloor (n_h+p_h-k_h+s_h)/s_h \rfloor * \lfloor (n_w+p_w-k_w+s_w)/s_w \rfloor ⌊(nh+ph−kh+sh)/sh⌋∗⌊(nw+pw−kw+sw)/sw⌋
可以发现之前的 s h s_h sh s w s_w sw 值为1 -
可以用padding和stride来指定填充和步幅
-
通常我们很少采用横纵不同的填充和步幅
# 高度填充0 宽度填充1 高度步幅3 宽度步幅4
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
0x04 通道
到目前为止我们讨论的都只是单输入通道,也就是灰度图像,比较简单的任务可以这么处理,但是一旦内容复杂起来,灰度图像很难比得上RGB三通道图像。
1.多输入单输出通道
两个通道的例子
- 每个输入通道有一个卷积核,对应做卷积运算,之后求和做单输出
- 输入 X : c i ∗ n h ∗ n w X: c_i*n_h*n_w X:ci∗nh∗nw
- 卷积核 W : c i ∗ k h ∗ k w W: c_i*k_h*k_w W:ci∗kh∗kw
- 输出 Y : m h ∗ m w Y: m_h*m_w Y:mh∗mw
2.多输入多输出通道
- 在多输入单输出的基础上,每个输入通道用多个卷积核进行卷积,可以输出多个通道结果
- 输入 X : c i ∗ n h ∗ n w X: c_i*n_h*n_w X:ci∗nh∗nw
- 卷积核 W : c o ∗ c i ∗ k h ∗ k w W: c_o*c_i*k_h*k_w W:co∗ci∗kh∗kw
- 输出 Y : c o ∗ m h ∗ m w Y: c_o*m_h*m_w Y:co∗mh∗mw
3.1*1卷积层
如果一个卷积层的卷积核是1*1大小的,那会导致输入和输出的大小不会变化,每次只看一个像素,不会识别空间模式,只起到融合通道的作用
图中有两个卷积核,通过1*1卷积融合三个输入通道后,输出两个融合后的特征图
可以看做,在每个输入通道的每个像素之间做全连接, c i c_i ci 个输入转换为 c o c_o co 个输出
4.总结
- 深度卷积神经网络的开始几层是在学习一些比较基础的特征,比如边、角,通过多输入多输出的组合不断上升到高层次不断组合简单特征,高层学习到的可能就是一些面(更具体更广泛)的信息
- 1*1的卷积对于单像素来说相当于全连接层
- 1*1卷积层可以控制通道数量和模型复杂度
- 输出通道数量是超参数
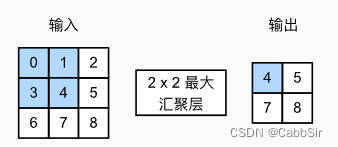
0x05 池化层
在我们检测边缘特征的时候,我们使用的是比较规则的0,1分布图像,但是现实中的图像往往不会有如此清晰规则的边缘信息,那么就希望我们的网络对于这种特征有一定的容错率,pooling层的意义就在于此。
与卷积操作比较相似的是,也需要进行滑动窗口,具体操作就是将这个窗口在图像上滑动,最大池化就是取这个窗口中的最大值保存,平均池化就是取平均值保存(有一种下采样的感觉)。
- 池化层不包含可以学习的参数
- 池化层也有填充和步幅
- 输入通道数 == 输出通道数
手动实现池化操作
import torch
from torch import nn
from d2l import torch as d2l
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y
X = torch.arange(30, dtype=torch.float32).reshape(5, 6)
# 验证操作
print(X)
print(pool2d(X, (2, 2)))
print(pool2d(X, (2, 2), 'avg'))
输出结果
tensor([[ 0., 1., 2., 3., 4., 5.],
[ 6., 7., 8., 9., 10., 11.],
[12., 13., 14., 15., 16., 17.],
[18., 19., 20., 21., 22., 23.],
[24., 25., 26., 27., 28., 29.]])
tensor([[ 7., 8., 9., 10., 11.],
[13., 14., 15., 16., 17.],
[19., 20., 21., 22., 23.],
[25., 26., 27., 28., 29.]])
tensor([[ 3.5000, 4.5000, 5.5000, 6.5000, 7.5000],
[ 9.5000, 10.5000, 11.5000, 12.5000, 13.5000],
[15.5000, 16.5000, 17.5000, 18.5000, 19.5000],
[21.5000, 22.5000, 23.5000, 24.5000, 25.5000]])