深度强化学习满足图神经网络:探索路由优化用例

摘要

近年来，深度强化学习(DRL)在决策问题上取得了巨大的进步。因此，在自动驾驶软件定义网络中，DRL似乎有望解决许多相关的网络优化问题(如路由)。然而，大多数最先进的基于drl的网络技术不能一般化，这意味着它们在训练中看到的网络拓扑中表现良好，但在新的拓扑上表现不佳。这一重要限制背后的原因是，现有的DRL网络解决方案使用标准的神经网络(例如，完全连接、卷积)，不适合学习图结构的信息。在本文中，我们提出将图神经网络(GNN)与DRL结合使用。GNN最近被提出用于图的建模，我们新颖的DRL+GNN架构能够学习和概括任意网络拓扑。为了展示其泛化能力，我们在一个基于sdn的光传输网络(OTN)场景中对其进行了评估，在该场景中，流量需求需要有效分配。我们的结果表明，我们的DQN+GNN代理能够在训练中从未见过的拓扑中取得出色的性能。

1.介绍

近年来，深度强化学习(Deep Reinforcement Learning, DRL)在决策和自动化控制问题上取得了显著进展[21,24]。在这种背景下，网络社区正在研究DRL作为网络优化(如路由)的关键技术，其目标是实现自动驾驶软件定义网络[19]。然而，现有的基于drl的解决方案在应用于不同的网络场景时，仍然不能一般化。这妨碍了DRL代理在面对训练中没有看到的网络状态时做出良好决策的能力。事实上，大多数现有的DRL组网方案只能在训练中看到的相同网络拓扑上操作[8,17]，因此，不能泛化和有效地操作看不见的网络拓扑。这种强大限制背后的主要原因是，计算机网络基本上是用图形表示的。例如，网络拓扑和路由策略通常是这样表示的。然而，最先进的提案[8,18,27,28]使用传统的神经网络(NN)架构(例如，全连接，卷积神经网络)，不太适合对图结构信息[4]建模。最近，图神经网络(GNN)[23]被提出对图进行建模和操作，以实现关系推理和组合泛化。换句话说，gnn有助于学习图元素之间的关系和组成它们的规则。gnn在网络建模和优化领域显示出前所未有的泛化能力[22,26]。

在本文中，我们提出了一种用于网络优化的开创性DRL+GNN架构。特别是，我们的新架构旨在优化网络路由，并能够在从未见过的任意拓扑上泛化。我们的DRL代理中集成的GNN的灵感来自于消息传递神经网络[12]，它成功地应用于解决了一个相关的化学问题。在我们的示例中，GNN被专门设计用于捕获关于通过网络拓扑流动的链路和流量之间关系的有意义的信息。

为了展示提出的DRL+GNN架构的泛化能力，我们在基于sdn的光传输网络(OTN)场景中对其进行了实验评估。特别是，DRL+GNN代理的任务是在通信请求到达时分配它们，使通过网络路由的通信流量最大化。评估结果表明，与最先进的DRL (SoA DRL)算法相比，我们的代理具有较强的泛化能力。特别是，我们在一个网络拓扑中训练了基于DRL的解决方案——DRL+GNN和SoA DRL代理——并在第二个网络拓扑中评估它们。结果表明，我们的DRL+GNN代理在新的拓扑结构中明显优于SoA DRL代理。此外，为了进一步测试提出的基于drl的架构的泛化能力，我们在一个包含136种不同现实世界网络拓扑的集合中对其进行了评估。结果表明，我们的代理能够在训练中从未见过的网络上取得出色的性能。

据我们所知，这是第一个基于drl的提案，它集成了一个GNN来实现网络优化问题的泛化。

2.背景

本文提出的解决方案结合了两种机器学习机制。

首先，我们使用图神经网络来模拟计算机网络场景。

其次，我们使用深度强化学习(Deep Reinforcement Learning)来构建一个代理，它学习如何按照特定的优化目标高效地运行网络。

2.1图神经网络

图神经网络是一种新颖的神经网络家族，旨在操作图结构的信息。它们在[23]中被引入，自[10,16,30]以来已经发展出许多变种。在它们的基本形式中，它们包括将一些初始状态与输入图的不同元素相关联，并考虑这些元素在图中如何连接而将它们组合起来。迭代消息传递算法更新元素的状态，并使用结果状态产生输出。要解决的问题的特殊性将决定哪种GNN变体更适合，这取决于所涉及的图元素(即节点和边)的性质。

消息传递神经网络(MPNN)[12]是一种著名的gnn类型，它应用迭代消息传递算法在图的节点之间传播信息。在消息传递步骤中(参见图1)，每个节点k接收来自其邻居(用N(k)表示)的所有节点的消息。将消息函数m(·)应用于图中节点对的隐藏状态，然后通过聚合函数进行组合，如求和(式1)，最后使用更新函数u(·)计算每个节点的新隐藏状态(式2)。

其中函数m(·)和u(·)可以通过神经网络学习。经过一定次数的迭代后，读取函数r(·)使用最终的节点状态为给定的任务产生输出。这个函数也可以通过神经网络实现，通常的任务是预测单个节点的属性(例如，节点的类)或图的全局属性。

在数据通常以图的形式结构化的多个领域中，gnn已经能够获得相关的性能结果[3,12]。由于计算机网络本质上是用图形来表示的，因此与传统的神经网络结构(如全连接NN、卷积NN等)相比，gnn在网络建模方面具有独特的优势，这是其设计的固有特点。最近的工作显示了它们在预测[22]网络性能方面的潜力，即使是在训练[26]时对网络拓扑进行预测时也是如此。

2.2深度强化学习

DRL算法的目标是学习一种长期策略，使优化问题中的目标函数最大化。DRL代理从白板开始。这意味着他们之前对他们所处的环境没有专业知识。他们通过探索状态和行动空间的迭代过程学习最优策略，并受到奖励函数的指导。状态空间和动作空间由一组状态(S)和一组动作(A)表示。给定一个状态s∈S, agent将执行一个动作a∈A，该动作产生向新的状态s∈S的过渡，并为agent提供奖励r。然后，目标是找到一个在一集结束时累计奖励最大化的策略。章节结束的定义取决于要解决的优化问题。这个优化问题可以建模为马尔可夫决策过程(MDP)。然而，寻找MDP的最优解需要评估所有可能的状态-动作对组合。

解决MDP的另一个选择是使用强化学习(RL)。Q-learning[31]是一个RL算法，它的目标是让代理学习一个策略π: S→A。该算法创建一个包含所有可能的状态和动作组合的表(也称为q表)。在训练开始时，表被初始化(例如，用0或随机值)，在训练期间，agent根据选择一个动作后获得的奖励更新这些值。这些值称为q值，表示从状态s应用动作a后的预期累积奖励，假设代理遵循在事件剩余时间学到的当前策略π。在训练过程中，使用Bellman方程(见方程3)更新Q值，其中r(s,a)为从状态s中选择动作a获得的奖励，Q(s’，a)为Q值函数，γ∈[0,1]为折现因子，表示未来获得奖励的重要性。

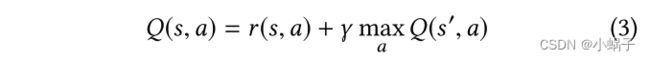深度Q-Network (Deep Q-Network, DQN)[20]是一种基于q-学习的更高级的算法，它使用深度神经网络(Deep Neural Network, DNN)来近似q值函数。随着q表尺寸的增大，q学习很难从高维状态空间和动作空间中学习策略。为了克服这个问题，他们提出使用DNN作为q值函数估计器。这使得我们能够依靠dnn的泛化能力来预估未被发现的状态和动作的q值。因此，一种非常适合理解和概括DRL代理的输入数据的神经网络对于代理在面对以前从未见过的状态(或环境)时的良好表现至关重要。此外，DQN使用经验回放缓冲区来存储过去连续的经验(即存储元组{s,a,r,s '})。在训练神经网络时，通过从经验回放缓冲区中随机采样来打破时间相关性。

3.网络优化场景

为一组流量需求找到最佳路由配置是一个np困难的问题[11]。这使得有必要探索替代解决方案(例如，启发式)，以负担得起的成本最大化性能。在本文中，我们探索了基于gnn的DRL代理在涉及不同网络拓扑的路由场景中操作和一般化的潜力。作为第一种方法，我们考虑光传输网络(OTN)[25]中的路由场景。特别地，我们考虑一个基于sdn的场景，其中DRL代理(位于控制平面)拥有当前网络状态的全局视图，并且必须在每一个流量需求到达时做出路由决策。这是一个相关的优化场景，在过去的几十年里，在光网络领域已经被研究，其中提出了许多解决方案[8,15,28]。

该问题可以描述为网络中一个经典的资源分配问题。在我们的OTN场景中，我们拥有一个拓扑，其中链路具有给定的容量，DRL代理接收需要实时分配的具有不同带宽需求的流量请求。一旦分配了流量需求，就不能释放或替换该需求的资源。因此，问题包括分配网络中的最大流量。

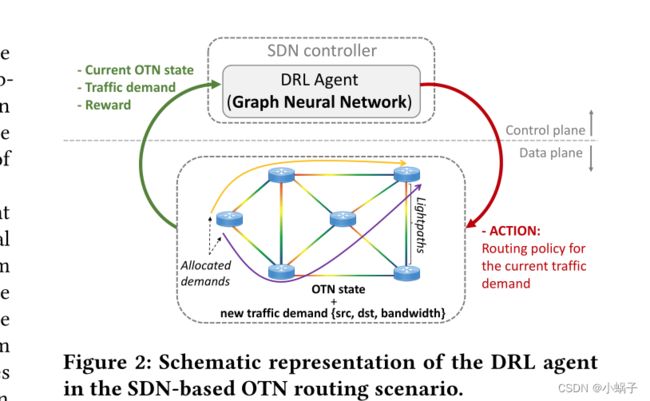
DRL代理运行在电域的层次上，在逻辑拓扑上，节点表示可重构的光添加-删除复用器(ROADM)节点，并连接一些预定义的光路径(见图2)。DRL代理接收一个由元组{src,dst,bandwidth}定义的流量需求，并负责通过一个特定的光路径序列(即端到端路径)路由流量需求，这些光路径连接源和目的地。在图2中，我们可以看到分配两个需求后的网络状态的图形表示。流量需求被视为ODU (Optical Data unit)的请求，其带宽需求见ITU-T建议书G.709[1]。

在这个场景中，路由问题被定义为为每个传入源目的流量需求找到最优路由策略。学习过程由一个目标函数来指导，目标函数的目标是在网络中长期分配最大的流量。当所选的端到端路径中所有光路径都有足够的可用容量时，我们认为需求分配是合理的。注意光路是逻辑拓扑中的链路/边。要求不过期，占位光路，直到一集的结尾。这对DRL代理来说意味着一项具有挑战性的任务，因为它不仅要确定网络上的关键资源(例如，潜在的瓶颈)，而且还要处理未来流量需求产生的不确定性。

4.基于gnn的DRL代理设计

在本节中，我们描述了本文提出的DRL+GNN代理。我们的DRL代理实现了DQN算法[20]，其中q值函数由GNN建模。从现在起，我们的代理称为DQN+GNN代理。在每个时间步，代理接收一个图结构的网络状态观察和一个流量需求作为输入。特别是，网络状态包括具有一些链路级特性(例如利用率)的拓扑结构。然后，GNN的目标是估计对当前网络状态下的新流量需求应用路由动作(a)的Q值Q(s, a)。

在我们的示例中，GNN构造了一个图表示，其中拓扑的链接是图实体。在这种表示中，考虑到输入链路级特性和要评估的路由动作，链路隐藏状态被初始化(详见4.1、4.2和4.3小节)。通过这种表示，可以根据图结构在链路隐藏状态之间运行一个迭代的消息传递过程。

在消息传递阶段的最后，GNN输出q值估计。这个q值在一组有限的动作(a)上进行评估，最后DRL代理选择q值更高的动作。然后在环境中应用选定的操作，产生到新的网络状态的转换。如果动作执行成功(即所有选择的链接都有足够的可用容量来支持新的需求)，则向代理返回正的奖励，否则情节结束，DRL代理收到等于0的奖励。

在培训阶段，使用ϵ-greedy探索策略[20]来选择代理应用的下一个操作。这意味着随机行为的执行概率为柱一，而q值较高的行为的选择概率为1-ϵ。

4.1环境

网络状态是由拓扑链路的特性来定义的，这些特性包括链路容量和链路间的关系。前者表示链路上的可用容量。后者是一种从图论中继承的中心性度量，它表明有多少路径可能穿过链接。特别地，我们用以下方式计算链路之间的连接:对于拓扑中的每一对节点，我们计算k条候选路径(例如，k条最短路径)，并且我们维护每个链路计数器，表示有多少条路径通过链路。因此，每条链路上的间隔是交叉链路的端到端路径数除以总路径数。

4.2Action set

在本节中，我们将描述如何在DQN+GNN代理中表示路由操作。请注意，每个源-目的地节点对可能的路由组合的数量通常会导致大型现实网络中的高维操作空间。这使得DRL代理的路由问题变得复杂，因为它应该估计所有可能的操作(即路由配置)的q值。为了克服这个问题，必须仔细设计动作集以降低维度。另外，为了利用GNN的泛化能力，动作应该以图的形式引入到agent中。这使得动作表示对节点和边缘置换不变量，这意味着，一旦GNN被成功训练，它应该能够理解任意图结构上的动作(即，在不同的网络状态和拓扑)。

考虑到上述情况，我们将每个源-目标对的操作集限制为k个候选路径。为了在路由流量的灵活性和评估所有可能操作的成本之间保持良好的权衡，我们为每个源-目标节点对选择k=4条最短路径(按跳数)的集合。这遵循[28]最初提出的标准。注意，根据要路由的流量需求的源节点和目标节点，操作集是不同的。

为了表示动作，我们在网络状态中引入它。特别地，我们考虑了一个附加的链路级特性，即应用路由动作后在链路上分配的带宽。该值对应当前需要分配的流量请求的带宽需求。同样，动作选择的路径中没有包含的链接也会将此特性设置为零。

由于我们的OTN环境具有各种离散带宽需求的有限数量的流量请求，我们用一个n元素的一热编码向量表示分配的带宽。图3演示了在一个简单的网络场景中链接的隐藏状态中这个特性的表示。从节点1到节点5的一个流量请求，流量需求为8个带宽单位，分配在节点{1,2,3,5}形成的路径上。总而言之，表1提供了链接隐藏状态中包含的特性的描述。这些值代表网络状态和动作，动作是建模qvalue函数Q(s, a)所需的输入。注意，隐藏状态的大小通常比隐藏状态中的特征数量更大。然后，一种常见的方法是用零值填充向量。

 

 链接可用容量

联系的中间状态

动作向量(带宽分配)

补零

4.3GNN架构

GNN模型基于消息传递神经网络[12]模型。在我们的示例中，我们考虑链接实体并在所有链接之间执行消息传递过程。该算法执行了T个消息传递步骤。如图4所示。开始时，算法遍历网络拓扑的所有链路。对于每个链路，它遍历其所有邻居，将链路特征与全连接NN相结合。根据GNN表示法，这些操作的输出称为消息。然后，为同一个节点及其邻居计算的消息使用元素求和进行聚合。最后，利用递归神经网络(RNN)，用新的聚合信息更新链路隐藏状态hLK。这个过程重复T次，在这个阶段的最后，得到的链路状态使用元素和进行聚合。最后，将计算结果通过全连接神经网络进行传递，并对该神经网络的Readout函数进行建模。后一个函数的输出是输入状态和动作的估计q值。

算法1给出了消息传递过程的形式化描述。该算法接收作为输入的链接的特征(xl)和输出q值(q)。从第1行开始的循环用链接的特征初始化链接的隐藏状态。之后，算法在T步中执行消息传递(第3-6行)。详细,每个链接l消息函数的m(·)方程1中描述的需要作为输入的隐藏状态链接hl和隐藏的邻居联系你好我∈N (l)。重复相同的过程对于所有链接的邻居l和执行所有图中的链接(l),遍历所有的链接后,输出向量是使用以聪明元素和聚合,产生新的特征向量为每个链接。然后利用更新函数u(·)将得到的向量Mt+1 l与各自之前的链路隐藏状态ht l结合起来。m(·)函数和u(·)函数由神经网络(分别为全连通神经网络和递归神经网络)学习。最后，更新函数u(·)的输出使用元素求和进行聚合(第7行)，将结果传递给一个全连接的神经网络，该网络对读出器R(·)进行建模。这将输出一个数值，表示输入状态和动作的q值。

4.4DRL Agent Operation

DRL代理通过与环境交互进行操作。在算法2中，我们可以观察到描述DRL代理操作的伪代码。一开始，我们通过将所有链接容量设置为最大值并计算链接之间的链接来初始化环境s。同时，环境产生一个流量需求，由元组{src,dst,bw}定义分配。我们还将累积奖励初始化为0，定义动作集大小并创建体验回放缓冲区(agent .mem)。之后，我们执行一个while循环(第6-19行)，当网络拓扑中有一些无法分配的需求时(即所选路径中至少有一个链路容量不足)，循环结束。第8行计算k=4条最短路径。对于每条路径，我们沿着形成路径的所有链接分配需求，并计算q值(第10-12行)。获得每个状态-操作对的q值后，使用ϵ-greedy探索策略选择下一个要应用的操作a(第13行)。然后，这个动作(即在第k条最短路径上进行分配)被应用到环境中，导致一个新的状态s '，一个奖励r和一个标志Done，表示是否有一些链接没有足够的能力来支持需求。另外，环境返回一个新的流量需求元组{src '，dst '，bw '}。关于状态转换的信息存储在经验回放缓冲区中(第16行)。此信息稍后将用于在agent .replay()调用(第18行)中训练GNN，该调用每M个训练迭代执行一次/。。。

5.实验结果

在本节中，我们培训和评估基于gnn的DRL代理，以在第3节中描述的基于sdn的OTN路由场景中有效分配流量需求。特别是，本节所做的实验主要是评估我们的DQN+GNN agent的泛化能力(第4节)。

5.1评价设置

我们使用Tensorflow实现了DQN+GNN代理。采用OpenAI Gym框架[7]实现DRL网络拓扑环境。源代码以及本文中提出的所有培训和评估结果都是公开的1。

我们在单一拓扑上训练DQN+GNN代理。使用的拓扑是14节点的NSFNet拓扑[13]，在1000个训练集期间对agent进行训练。对于每个迭代，我们分别执行100和50个训练和测试片段。选择测试得分最高的模型来进一步评估不同的拓扑结构，并与最先进的解决方案进行比较。

我们考虑3种类型的流量需求，它们的带宽需求用ODU0信号的倍数[1]表示(分别为8、32和64个ODU0带宽单位)。当DRL代理分配一个请求时，如果分配正确，它会收到一个即时的奖励，即当前流量请求的带宽，否则奖励为0。通过统一选择源目的节点对和流量需求带宽，每一步生成流量需求。这对于DQN+GNN代理来说是一个具有挑战性的优化场景，因为新需求的生成是随机的。因此，它不能利用来自流量分布的有用信息来设计一个适当的长期策略。

为我们的DQN+GNN agent选择合适的梯度优化算法和超参数值进行了初步实验。在我们的实验中，我们选择大小为25的链接的隐藏状态hl。请注意，隐藏状态的大小与它们可能编码的信息量有关。对于更大的网络拓扑，可能需要为隐藏状态向量使用更大的尺寸。在每一次向前传播中，我们使用32个样本批次执行T=8个消息传递步骤。使用的优化器是一个随机梯度下降[5]方法与Nesterov动量[29]。超参数的学习速率为10−4，动量为0.9。对于ϵ-greedy探索策略，我们从柱一=1.0开始，该值在10次训练迭代中保持。之后，柱一每隔两期呈指数衰减。为了稳定学习过程，我们每2集重新训练GNN模型的权重，每次我们使用5批(32个样本)从经验缓冲。经验回放缓冲区的大小被设置为存储5000个样本，它被实现为FIFO队列:一旦它满了，最古老的经验将被删除。

5.2方法

为了评估我们的DQN+GNN agent的性能，我们设计了广泛的评估实验。在第一个实验中，我们的目标是比较我们的DQN+GNN代理与最先进的基于drl的解决方案的性能和泛化能力。为此，我们参考[28]中提出的基于drl的解决方案。我们评估两种基于drl的解决方案在网络拓扑中没有在训练中看到。在第二个实验块中，我们评估了基于从Internet Topology Zoo数据集[14]中提取的真实网络拓扑的DRL+GNN架构的性能和泛化能力。

我们将我们的代理与最先进的基于drl的解决方案[28]、负载平衡路由策略(LB)和理论流体模型(标记为理论流体)进行比较。LB策略在k=4条候选最短路径中随机选择一条路径。流体模型是一种理论方法，它认为交通需求可以按可用容量的比例分成k=4个候选路径。该路由策略的目的是避免链路拥塞。例如，可用容量低的路径将承载来自新需求的一小部分流量。注意，这个模型是不可实现的，因为在实际的OTN场景中，ODU需求不能分割。但是，我们使用它作为参考来衡量我们的DRL代理在不同网络场景中的性能。

5.3训练

我们在14节点NSFNet拓扑[13]的OTN路由场景中训练DRL代理，其中我们认为链路代表容纳200个ODU0信号的光路。请注意，容量在链路的两个方向上共享，不同流量需求的带宽用ODU0信号的倍数表示(即8、32或64个ODU0带宽单位)。在训练过程中，代理接收流量需求，并将其分配到操作集中k=4条最短路径中的一条上。我们运行1000次训练迭代，将状态转换、执行的操作和获得的奖励存储在经验回放缓冲区中。我们通过从经验缓冲区中采样来训练GNN，并使用q值作为输出标签(定义在公式3中)。为了进行评估，我们运行了50集，并计算所有集获得的平均累积奖励。

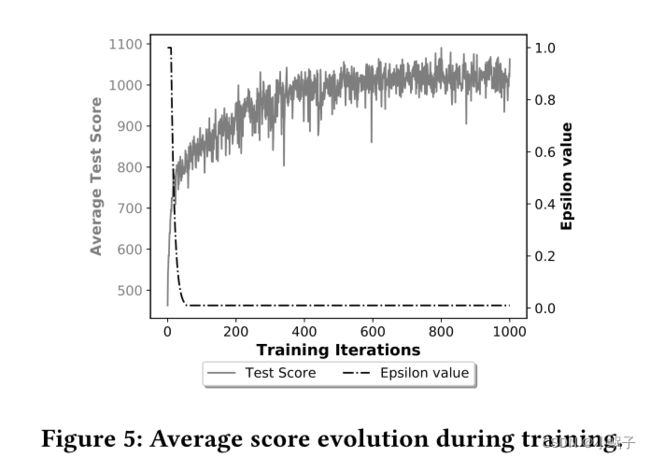
在图5中，我们展示了DQN+GNN agent在50集的平均评价得分。我们可以观察到，在大约600次训练迭代后，学习保持稳定。我们还展示了在培训期间用于ϵ-greedy探索策略的柱一参数的演变。我们可以观察到，当柱夫一开始衰减时(即在第10次迭代前后)，代理的得分会不断稳定地增加。这表明，在这一点上，GNN已经能够产生足够好的q值估计，使更智能的探索状态和行动，这有助于代理加快学习过程。

训练中的平均分数演变

5.4对最先进的基于drl的解决方案进行评估

在本次评价实验中，我们选取了训练中得分最高的DQN+GNN agent。我们将其与最先进的基于drl的解决方案进行比较。特别地，我们调整了[28]中提出的解决方案，使其在链路在两个方向共享其容量的场景中运行。

我们在两个网络场景中训练最先进的DRL代理的两个不同实例:14节点的NSFNet和24节点的Geant2拓扑[2]。在我们的评估中，我们做了1000个随机流量生成的实验，以提供有代表性的结果。请注意，本文中提出的DQN+GNN代理和最先进的DRL解决方案都是在相同的随机生成需求列表上进行评估的。

我们进行了两个实验来比较我们的DQN+GNN的性能与最先进的DRL得到的结果。在第一个实验中，我们将DQN+GNN代理与在NSFNet上训练的最先进的DRL代理、LB路由策略和理论流体模型进行评估。我们评估了NSFNet拓扑上的四种路由策略，并比较了它们的性能。在图6a中，我们可以观察到一个包含1000多个评价实验结果的bloxplot，图6c显示了相对于流体模型获得的相对分数的累积分布函数(CDF)。从这些结果中，我们可以断言，我们的DQN+GNN代理在大约80%的实验中优于最先进的基于drl的解决方案。在第二个实验中，我们评估了相同的模型(DQN+GNN、LB和theory Fluid)，但在这个实验中，我们使用了在Geant2上训练的最先进的DRL agent。得到的箱线图如图6b和6d评价样本的CDF。同样，我们代理在60%的情况下性能更好。因此，我们可以说我们的DQN+GNN代理比传统的基于drl的解决方案具有更好的性能。

我们进行了另外两个实验来比较我们的DQN+GNN代理的泛化能力。在第一个实验中，我们评估我们的DQN+GNN代理(在NSFNet上训练)与最先进的DRL代理(在Geant2上训练)，并在NSFNet拓扑上评估它们。在图7a中，我们可以观察到一个包含1000多个评价实验的评价结果的箱线图。图7c显示了该代理相对于在Geant2上训练的最先进的DRL代理的相对得分的CDF。从这些结果中，我们可以观察到我们的DQN+GNN代理明显优于最先进的DRL代理。例如，在大约80%的实验中，性能改进超过20%。在第二个实验中，我们评估相同的DQN+GNN代理(在NSFNet上训练)和最先进的DRL代理(在NSFNet上训练)，并评估Geant2拓扑上的两个代理。由此产生的箱线图可以在图7b和图7d中对应的CDF中看到。结果表明，在这种情况下，我们的代理也优于最先进的DRL代理。在这种情况下，与最先进的方案相比，在80%的实验中，我们的DRL代理实现了45%以上的性能改进。这些结果表明，虽然提出的DQN+GNN代理能够在不可见的Geant2拓扑中一般化并取得出色的性能(图7b和7d)，但最先进的DRL代理在应用于训练中没有看到的拓扑时表现较差。这就暴露了后一种基于drl的解决方案与本文提出的agent相比缺乏泛化能力。