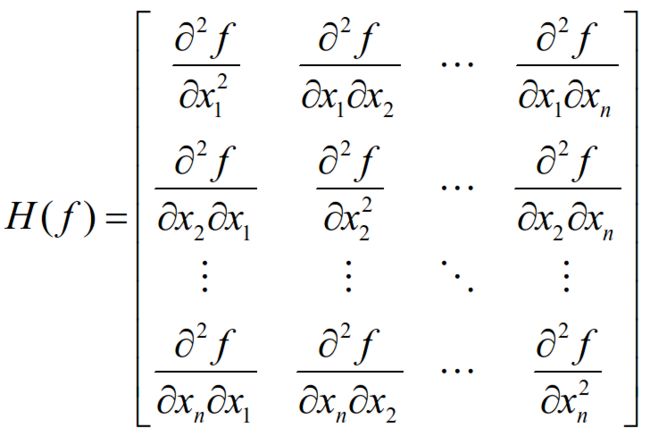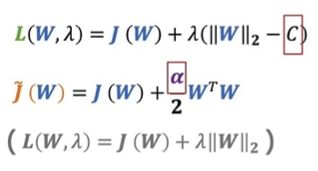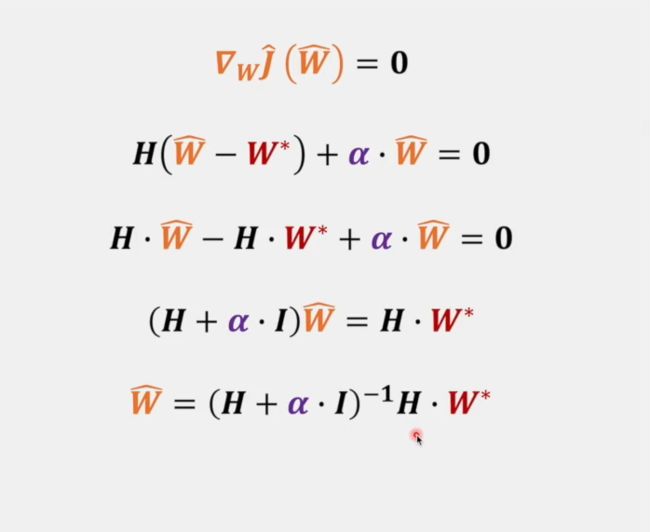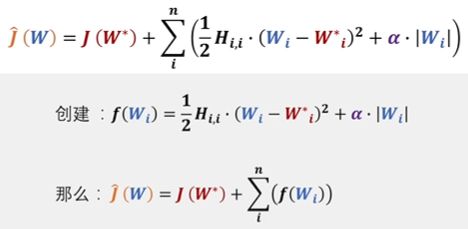【学习笔记】深刻理解L1和L2正则化
深刻理解L1和L2正则化
学习视频:BV1Z44y147xA、BV1gf4y1c7Gg、BV1fR4y177jP
up主:王木头学科学
L1、L2正则化即使用L1、L2范数来规范模型参数。
凡是减少泛化误差,而不是减少训练误差的方法,都可以称为正则化方法。
通俗来说,即凡是能减少过拟合的方法,都是正则化方法。
补充概念
范数
可以理解为把空间中两个点的距离这个概念给拓展。
如权重W为一个高维的向量,或高维空间中的一个点。这个点到原点的距离
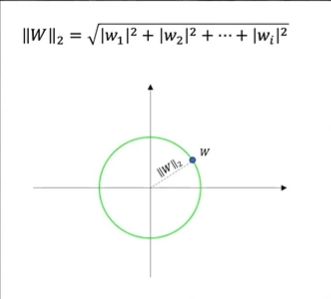
若为欧式距离,则为L2范数,其公式和图像如下:
即使用高维的勾股定理计算距离。如果将L2范数相同的点都画出来,则会形成一个以原点为圆心,半径为L2范数的圆。
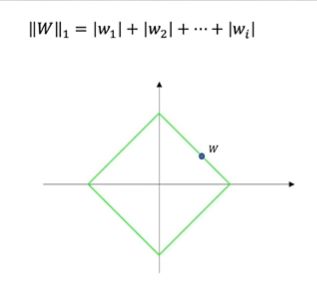
若为曼哈顿距离,即对坐标值直接取绝对值,则为L1范数,其公式和图像如下:
将L1范数相同的点画出来,组成的图形为一个中心在原点且偏转45°的正方形。
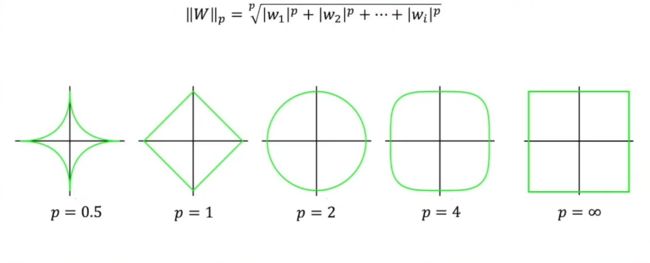
在正则化中,通常只用到L1、L2范数,但还有其他范数,如Lp范数。
当 0
凸集
参考【学习笔记】直观理解拉格朗日函数中内容。
黑塞(Hessian)矩阵
黑塞矩阵(Hessian Matrix),又译作海森矩阵、海瑟矩阵、海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。黑塞矩阵常用于牛顿法解决优化问题,利用黑塞矩阵可判定多元函数的极值问题。在工程实际问题的优化设计中,所列的目标函数往往很复杂,为了使问题简化,常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。
为什么我们要引入L1、L2正则化?
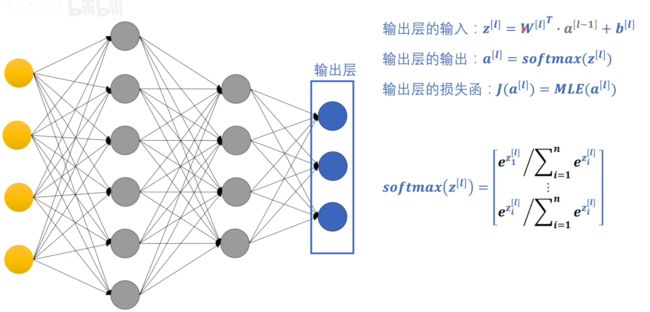
我们知道,通过训练迭代,一定能找到一组 W W W 和 b b b 使得输出层的损失函数最小。但就算我们得到的损失值是相同的,其对应的 W W W 和 b b b 也并不是唯一的,以下图为例:
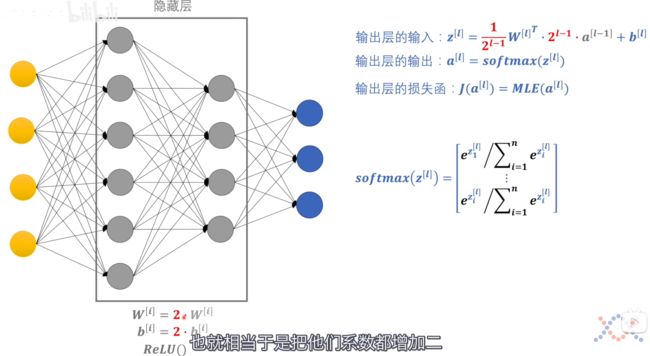
如果我们将隐藏层中的系数都增加到原来的两倍,则最后相当于输入层的输入里的变量系数增加了 2 l − 1 2^{l-1} 2l−1 倍,我们同时将 W W W 缩小 2 l l − 1 2^{ll-1} 2ll−1 倍,最后的结果依然是 z [ l ] z^{[l]} z[l],其对应的损失函数的值是不变的。
这就代表我们训练出来的 W W W 和 b b b 的值非常依赖于他们的初始值。如果初始值较大,则最后达到损失函数最小值得出来的 W W W 和 b b b 的值较大;而另一种情况,在损失函数收敛到相同的最小值时,可能得到的 W W W 和 b b b 的绝对值相对来说较小。
如果我们得到的参数较大,那么神经网络在面对新数据时,将会得到一个较大的结果。新数据中的误差和噪声经过大参数相乘以后将会被放大,这会严重影响最后的判断结果。所以我们才要将参数限定在一定的范围内。
由于神经网络模型主要由权重 W W W 所影响,所以正则化只关注权重而不关注偏置 b b b。
拉格朗日乘数法角度
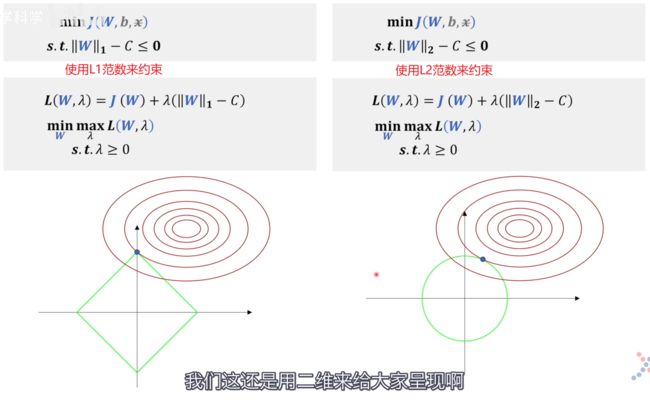
限制权重 W W W 的范围相当于是给参数规定可行域范围,而这正是拉格朗日乘数法所擅长的。
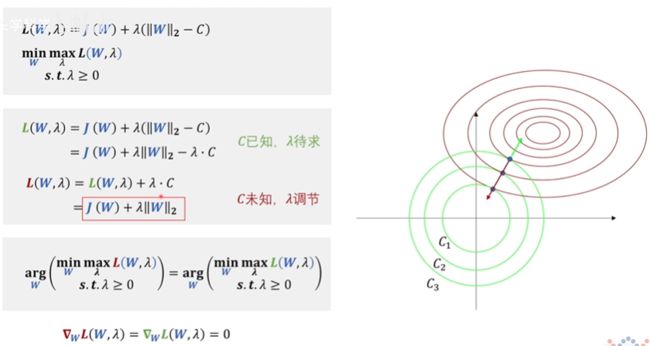
红色的 L ( W , λ ) L(W,\lambda) L(W,λ) 是我们熟知的L2正则化的公式。由于绿色的 L ( W , λ ) L(W,\lambda) L(W,λ) 和红色的 L ( W , λ ) L(W,\lambda) L(W,λ) 二者求梯度相同且需等于0,我们根据此来求 W W W 的值。虽然二者的最值可能不同(红色 m a x L ( W , λ ) max L(W, \lambda) maxL(W,λ) 不一定等于绿色 m a x L ( W , λ ) max L(W,\lambda) maxL(W,λ)),但是得到的参数 W W W 却是相同的。
所以 L2 正则化 和 用拉格朗日乘数法给 W W W 加一个约束范围 这两个问题是等价的。
直观理解,两个公式中的 C C C 即代表相同 L2 范数到原点的距离,即绿色圆的半径。可是在红色的 L ( W , λ ) L(W,\lambda) L(W,λ) 中我们消去了 C C C ,那么该如何控制绿色圆的半径呢?
答案就是通过 λ \lambda λ 来调节约束条件梯度的大小与方向,使得其与损失函数的梯度大小相等、方向相反,这样他们相加才能等于0,得到最后一行的公式,亦可知
λ = 损 失 函 数 的 梯 度 约 束 条 件 的 梯 度 \lambda = \frac{损失函数的梯度} {约束条件的梯度} λ=约束条件的梯度损失函数的梯度
得到了 λ \lambda λ ,就可以确定具体的极值点在哪里。
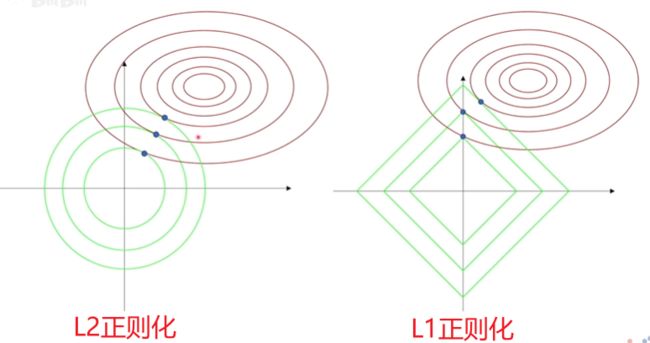
由图像我们可以直观的看出,L1正则化的极值点多在坐标轴上,这也是L1正则化带来稀疏性的体现,在数值上,即 W W W 在某些项有值,而其他项均为0;在特征上,他将特征与特征之间的关系进行解耦,使得只有特定的特征起作用,让问题简化,减少了过拟合的可能。
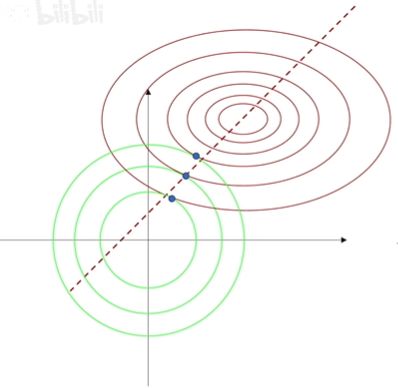
在神经网络中,最值不一定是一个点,而可能是一条路径。只要最终我们收敛在这条路径上任何一个点,都算是达到最值点了。
权重衰退角度
在训练过程中,我们依靠梯度下降法对权重进行更新。引入正则化后,损失函数加入正则项 α 2 W T W \frac{\alpha}{2} W^TW 2αWTW (其与 λ ∥ W ∥ 2 \lambda \Vert W \Vert_2 λ∥W∥2 等价),在梯度更新中也加入了正则项的梯度 η ⋅ α ⋅ W \eta \cdot \alpha \cdot W η⋅α⋅W ,经过调整后得到红色框中的式子。
根据权重 W W W 的系数 ( 1 − η ⋅ α ) (1-\eta \cdot \alpha) (1−η⋅α) 可以看出,在学习率和 α \alpha α 两个超参数相乘大于0小于1时,权重 W W W 在每次更新时,都会进行缩小,这便是权重衰减。
这时我们再去理解这两个式子,式(1)中 C C C 为超参数,相当于我们已经知道权重在哪个范围内取值比较好;
式(2)中 α \alpha α 为超参数,相当于我们不知道权重在哪个范围内取值较好,而是设定像学习率一样的衰减率,通过不断训练,一步一步学习,最后找到一个合适的范围。
总之,权重衰减即增加了一个惩罚项,在每次学习过程中不断惩罚权重,以保证权重不会取值太大。
L2正则化
L2正则化相对来说简单一些,我们先以它为例。
损失函数 J ( W ) J(W) J(W) 经过泰勒展开得到第一行的式子。
其中 H H H 为黑塞矩阵,代表损失函数的二阶导数。 W ∗ W^* W∗ 为损失函数的最值,故 ∇ W J ( W ∗ ) = 0 \nabla_W J(W^*) = 0 ∇WJ(W∗)=0 。
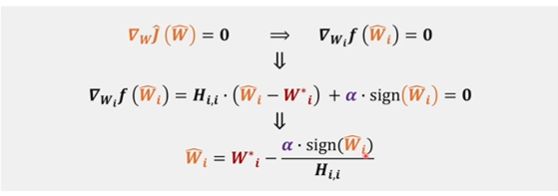
针对这个公式:
∇ w J ^ ( W ) = H ( W − W ∗ ) + α ⋅ W \nabla_w \hat J(W) = H(W-W^*)+\alpha \cdot W ∇wJ^(W)=H(W−W∗)+α⋅W
假设 W = W ^ W=\hat W W=W^ 时,达到正则化后的损失函数的最值,即 ∇ w J ^ ( W ^ ) = 0 \nabla_w \hat J(\hat W) = 0 ∇wJ^(W^)=0,则可推出:
对于 W ∗ W^* W∗ 前的系数 ( H + α ⋅ I ) − 1 H (H+\alpha \cdot I)^{-1}H (H+α⋅I)−1H 我们还需要进行变换,这里需要用到黑塞矩阵的性质。由于黑塞矩阵是对称矩阵,而所有对称矩阵都可以表示为 H = Q Λ Q T H = Q\Lambda Q^T H=QΛQT ,其中 Λ \Lambda Λ 是对角矩阵,而 Q Q Q 是正交基矩阵,即
Λ = [ λ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ λ n ] Q = [ e 1 0 ⋯ 0 0 e 2 ⋯ 0 ⋯ ⋯ ⋯ ⋯ 0 0 ⋯ e n ] Q T = Q − 1 ⇒ Q T Q = Q Q T = I \Lambda = \begin{bmatrix} \lambda_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_n \end{bmatrix} \\ Q = \begin{bmatrix} e_1 & 0 & \cdots & 0 \\ 0 & e_2 & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & e_n\end{bmatrix} \\ Q^T = Q^{-1} \Rightarrow Q^TQ = QQ^T = I Λ=⎣⎢⎡λ1⋮0⋯⋱⋯0⋮λn⎦⎥⎤Q=⎣⎢⎢⎡e10⋯00e2⋯0⋯⋯⋯⋯00⋯en⎦⎥⎥⎤QT=Q−1⇒QTQ=QQT=I
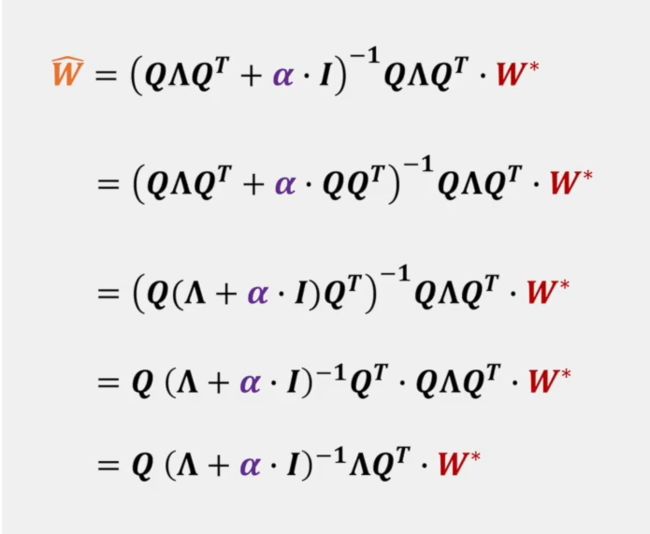
替换后可得以上式子。其中 Q Q Q 我们可以忽略,它只是表示你在哪个坐标系下进行表达。最总得到数量关系为:
W ^ i = λ i λ i + α W i ∗ \color{orange}\hat W_i \color{black} = \frac{\lambda_i}{\lambda_i + \alpha}\color{red}W^*_i W^i=λi+αλiWi∗
L1正则化
我们的目的是要找到 J ^ ( W ) \hat J(W) J^(W) 的最值,但是第一行我们无法继续处理,所以我们需要一些简化,对此,我们假设如下:
如下的推理为近似定量的结果。
我们将括号内的式子放入 f ( W i ) f(W_i) f(Wi) 做一下简化,要求 J ^ ( W ) \hat J(W) J^(W) 的最值,就要求导求它的梯度,即
其中 s i g n ( W ^ i ) sign(\hat W_i) sign(W^i) 为 W ^ i \hat W_i W^i 的符号,他不和具体的 W ^ i \hat W_i W^i 的数值有关系。我们主要看最后一行的式子:
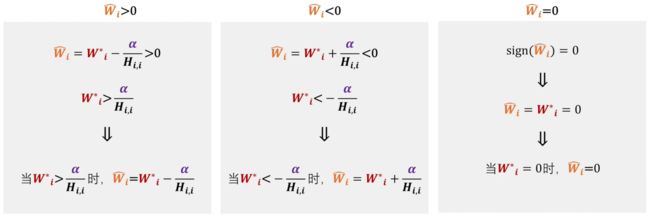
对于 W ^ i \hat W_i W^i 的取值情况有三种:
对于 − α H i , i < W i ∗ < α H i , i -\frac{\alpha}{H_{i,i}} \lt W^*_i \lt \frac{\alpha}{H_{i,i}} −Hi,iα<Wi∗<Hi,iα 的情况,我们设蓝色的 W i W_i Wi 为变量,红色的 W ∗ W^* W∗ 为参数,在上述范围内,求橙色的 W ^ i \hat {W}_i W^i 的值。
最终我们将上述分析结果整理,得到以下式子:
其中,这一部分很好的体现了L1正则化为什么能带来稀疏性,它将在此范围的的损失函数的最小值值强行拉至0这一点上。
贝叶斯概率角度
有时间待补充…
总结
总的来说L1用于降维,将对分类影响最小的特征权重降为0。L2是对 W W W 各维度缩减,防止 W W W 不停按比例放大。