使用柏林噪声生成游戏地图（一维和二维实现）

大家好，我是CuddleSabe，目前大四在读，深圳准入职算法工程师，研究主要方向为多模态（VQA、ImageCaptioning等），欢迎各位佬来讨论！
我最近在有序地计划整理CV入门实战系列及NLP入门实战系列。在这两个专栏中，我将会带领大家一步步进行经典网络算法的实现，欢迎各位读者（da lao）订阅

导学

自然界中很多事物是分形的。它们有着很多层次细节。最平常的例子是山峰轮廓。它包含着高度上的很大变化（山峰），中等变化（丘陵），小的变化（砾石），微小变化（石头）…你可以继续想象。观察几乎所有事物：片状分布于田间草，海中的波浪，蚂蚁的运动方式，树枝的运动，大理石的花纹，风。所有这些现象表现出了同一种的大小的变化形式。柏林噪声函数通过直接添加一定范围内，不同比例的噪声函数来重现这种现象。

白噪声

当我们使用随机数去填充一个二维数组的时候，我们会得到一个如下的白噪声:

白噪声看起来就像电视机上面的雪花一样，其中不包含任何信息，没有办法达到我们用来生成地图的需求。

回顾正弦函数的一些定义

我们针对正弦函数有如下定义，还记得吗：

• 振幅 (amplitude)
• 频率 (frequency)
• 波长(wavelength)

相信对于诸如sin，cos等周期函数的上面定义，大家已经很熟悉了。但是有一个问题：针对非周期函数，我们如何定义上述参数？
这里我们针对非周期函数做出如下参数定义：

• 振幅 (amplitude)：所使用的随机函数理论上能生成的最大值
• 频率 (frequency) ：分周期函数的采样点的间隔
• 波长(wavelength)：频率的倒数

生成噪声曲线的过程

其中的采样如上图所示，在生成随机函数曲线之前，我们需要获得一些采样点（一般为均匀间隔，可以使用整数）；在获得采样点之后，我们再对函数进行非线性插值获得一个光滑的曲线。注意，我们现在只获得了一个曲线而不是柏林噪声，我们仍需要继续生成不同频率和振幅的曲线并将它们相加才能获得我们最终想要的东西（神奇的分形思想！！）

总过程描述如下（以一维为例）：

均匀采样获得采样点

确定频率和振幅参数

使用获得的参数对采样点进行随机数赋值

得到一条函数曲线

将所有函数曲线相加

一维柏林噪声

经过上述过程描述，相信大家已经对其思想有一个基本了解了。但我们仍需确定一件事情：如何确定频率和振幅参数？
这里我们定义一个新的参数：Persistence（持续度）（0-1）
我们给持续度赋值后，可以得到：

• 频率 = $2^i$
• 振幅 = $持久{度}^i$
  其中$i$代表了现在是生成的第几条函数。
  可以看到，随着$i$的增大，振幅会越来越大，函数的频率也会越来越高，波峰越来越小。且持久度越小，最后得到的结果总体波动较小。可视化结果如下：
  
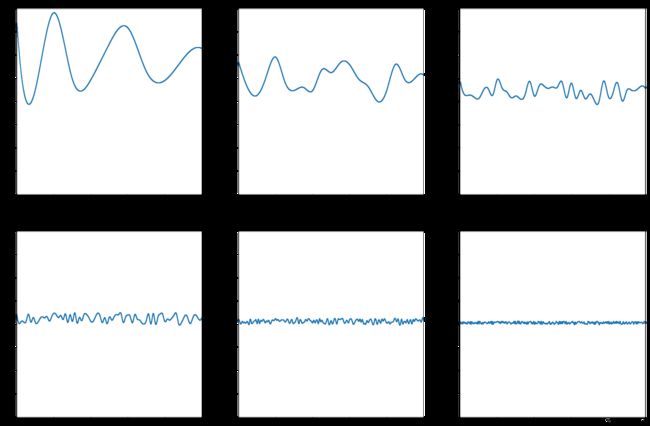
  我们将其相加，得到最终结果：
  
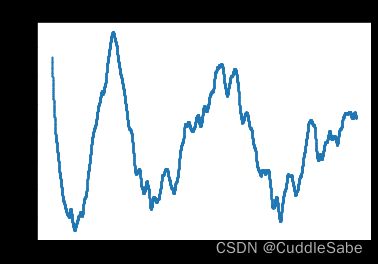
  可以看到，一开始生成的几条曲线振幅较大，频率较小。如果将其比作山的话，其代表了山的总体趋势。而后面的几条曲线则分别代表了诸如小山谷、石头等变化较小的部分。

经过上述分析，我们现在编写一维柏林噪声的代码。

start = 0
end = 10
persistence = 1/2
fineness = 0.001
layer_num = 6

def cubic_interpolate(input_x, input_y, fineness, frequent, amplitude):
    x = []
    y = []
    length = len(input_x)
    cubic_func = interp1d(input_x, input_y, kind = 'cubic')
    num = int((end - start)/ fineness)
    for inter_x in list(np.linspace(start, end, num)):
        inter_y = cubic_func(inter_x)
        x.append(inter_x)
        y.append(inter_y)
    return x, y

plt.figure( figsize=(30,20) )
perlin_y = list(np.zeros(int((end-start)/fineness)))

for i in range(layer_num):
    plt.subplot(2, 3, i+1)
    amplitude = persistence**i
    frequent = 2**i
    wavelength = 1 / frequent
    num = int((end - start)/ wavelength + 1)
    x = np.linspace(start, end, num)
    y = []
    for index, data in enumerate(x):
        random.seed(data)
        noise_y = random.uniform(0, amplitude)
        y.append(noise_y)
    cubic_x, cubic_y = cubic_interpolate(x, y, fineness, frequent, amplitude)
    layer_smooth_func = interp1d(cubic_x, cubic_y, kind = 'cubic')
    for index, perlin_x in enumerate(list(np.linspace(start, end, int((end-start)/fineness)))):
        perlin_y[index] += layer_smooth_func(perlin_x)
    plt.title("a={:.2f} f={:d}".format(amplitude, frequent))
    plt.scatter(cubic_x, cubic_y, s=1)
    plt.axis([start, end, -1, 1])
plt.show()

plt.title("Perlin Noise(Cubic)")
plt.scatter(list(np.linspace(start, end, int((end-start)/fineness))), perlin_y, s=1)
plt.show()

二维柏林噪声生成地图

同理，我们可以将其拓展到二维地图的生成，代码如下：

%matplotlib inline
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
import numpy as np
import random
import cv2

persistence = 1 /2
block = 3
layer_num = 5

layers = []
for i in range(1, layer_num+1):
    layers.append(np.zeros((3**i, 3**i)))
for layer in layers:
    print(layer.shape)

def random_fill(layer, amplitude):
    for i in range(layer.shape[0]):
        for j in range(layer.shape[1]):
            layer[i][j] = random.uniform(0, amplitude)

for i, layer in enumerate(layers):
    random_fill(layer, persistence**i)
    layers[i] = cv2.resize(layer, (block**layer_num, block**layer_num), interpolation=cv2.INTER_CUBIC)

game_map = np.zeros((block**layer_num, block**layer_num))
for layer in layers:
    game_map += layer

plt.imshow((game_map*255).astype("int8"))

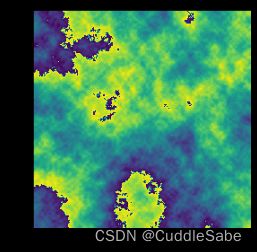
上述持久度参数设置为1/2，叠加层数分别为3和5。可以看出，其生成效果已经非常近似于海战游戏地图。（大家可以多调节参数看看效果w）