AQI空气质量分析与预测
AQI分析与预测
背景信息
AQI全称是Air Quality Index,指空气质量指数,用来衡量空气清洁或者污染的程度,值越小,表示空气质量越好。
本文的分析目标
一、描述性统计
- 哪些城市的空气质量较好/较差?
- 空气质量在地理位置分布上,是否具有一定的规律?
二、推断统计
- 临海城市的空气质量是否优于内陆城市?
三、相关系数分析
- 空气质量主要受哪些因素的影响?
四、区间估计
- 全国城市空气质量普遍处于哪种水平?
五、统计建模
- 怎样预测一个城市的空气质量?
本文理论基础可参考:描述性统计、参数估计和假设检验
https://xxmdmst.blog.csdn.net/article/details/115410809
本文目录:
文章目录
- AQI分析与预测
-
- 背景信息
- 本文的分析目标
- 导包并读取数据集
- 分析流程
- 数据清洗
-
- 缺失值处理
- 异常值
-
- 异常值探索
-
- 异常数据可视化
- 3倍标准差找出异常值
- 基于箱线图的规则找出异常值
- 异常值处理的方式
-
- 对数转换
- 边界值替换
- 分箱离散化
- 重复值处理
- 数据分析
-
- 哪些城市的空气质量较好/较差?
-
- 空气质量最好的5个城市
- 空气质量最差的5个城市
- 全国城市的空气质量
-
- 城市空气质量的等级统计
- 全国空气质量等级分布
- 临海城市的空气质量是否优于内陆城市?
-
- 数量统计
- 分布统计
- 差异检验:两样本t检验
- 关于t分布
- 空气质量主要受哪些因素影响?
-
- 多图矩阵
- 相关系数
- 空气质量指数均值的验证
- 对空气质量进行预测
-
- 数据转换
- 基础模型
- 临界值替换异常值
- 特征选择
- 分箱离散化
- 残差图分析
- 结论
导包并读取数据集
导包并读取数据:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")
plt.rcParams["font.family"] = "SimHei"
plt.rcParams["axes.unicode_minus"] = False
data = pd.read_csv("data/data.csv")
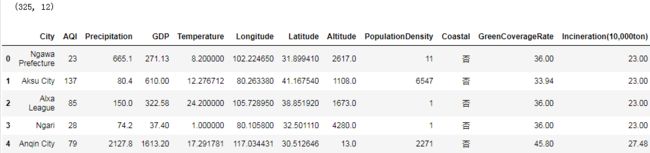
print(data.shape)
data.head()
数据集描述:
- City:城市名
- AQI:空气质量指数
- Precipitation:降雨量
- GDP:人均生产总值
- Tempearture:温度
- Longitude/Latitude:经/纬度
- Altitude:海拔高度
- PopulationDensity:人口密度
- Coastal:是否沿海
- GreenCoverageRate:绿化覆盖率
- Incineration(10,000ton):焚烧量(w吨)
数据集下载地址:https://gitcode.net/as604049322/blog_data
分析流程
- 明确需求与目的
- 数据收集:内部数据、购买数据、爬取数据、调查问卷等。
- 数据预处理
- 数据清洗:缺失值、异常值、重复值
- 数据转换
- 数据分析:
- 描述分析
- 推断分析
- 数据建模:特征工程、超参数调整等。
- 数据可视化
- 编写报告
数据清洗
缺失值处理
对于缺失值,我们可以使用如下方式处理:
- 删除缺失值:适合缺失值数量相对很少时。
- 填充缺失值:
- 数值变量
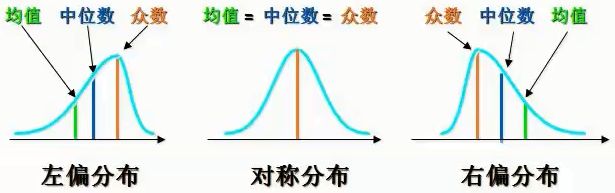
- 均值填充:适合非偏态分布的数据。
- 中值填充:适合偏态分布的数据。
- 类别变量
- 众数填充
- 空值单独作为一个类别
- 数值变量
偏态分布:
参考:https://xxmdmst.blog.csdn.net/article/details/115410809#t3
额外处理:
- 缺失值小于20%可以直接填充
- 缺失值在20%-80%时,填充变量后同时增加一列,标记该列是否缺失,参与后续建模。
- 缺失值大于80%,不使用原始列,标记该列是否缺失,参与后续建模。
查看缺失值数量:
data.isnull().sum(axis=0)
City 0
AQI 0
Precipitation 4
GDP 0
Temperature 0
Longitude 0
Latitude 0
Altitude 0
PopulationDensity 0
Coastal 0
GreenCoverageRate 0
Incineration(10,000ton) 0
dtype: int64
查看含缺失值列数据的偏度和分布:
print(data.Precipitation.skew())
sns.histplot(data.Precipitation, stat="density", kde=True)
plt.title("分布密度图")
0.27360760671177387
数值型变量,数据呈现一定的右偏,所以使用中位数填充比均值填充更佳。
对缺失值进行中位数填充:
data.Precipitation.fillna(data.Precipitation.median(), inplace=True)
data.isnull().sum()
City 0
AQI 0
Precipitation 0
GDP 0
Temperature 0
Longitude 0
Latitude 0
Altitude 0
PopulationDensity 0
Coastal 0
GreenCoverageRate 0
Incineration(10,000ton) 0
dtype: int64
异常值
异常值探索
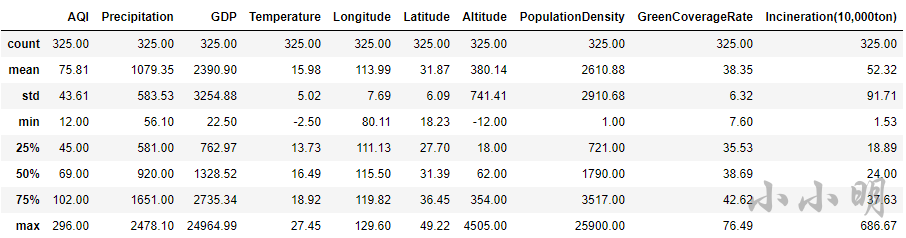
查看数据集的统计信息:
data.describe().round(2)
查看数据集的偏度:
data.skew(numeric_only=True)
AQI 1.198754
Precipitation 0.273608
GDP 3.761428
Temperature -0.597343
Longitude -1.407505
Latitude 0.253563
Altitude 3.067242
PopulationDensity 3.125853
GreenCoverageRate -0.381786
Incineration(10,000ton) 4.342614
dtype: float64
可以看到GDP和人口密度等都出现了严重的右偏分布,意味着存在极大的异常值。
异常数据可视化
我们可视化这两列的分布情况:
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
sns.histplot(data.GDP, stat="density", kde=True, ax=ax[0])
sns.histplot(data.PopulationDensity, stat="density", kde=True, ax=ax[1])
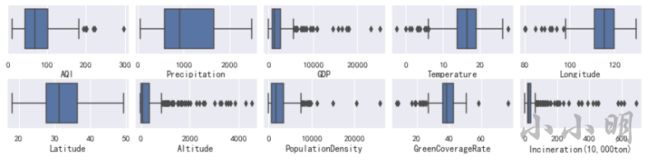
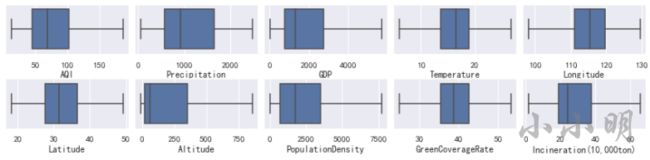
我们可以通过箱线图查看除了经纬度以外所有数值列的异常值情况:
fig, ax = plt.subplots(2, 5)
# wspace左右距离,hspace上下距离
plt.subplots_adjust(wspace=0.05, hspace=0.5)
fig.set_size_inches(15, 3)
for i, c in enumerate(data.select_dtypes("number").columns):
row, col = i//5, i % 5
sns.boxplot(data=data, x=c, ax=ax[row, col])
通过箱线图可以看到只有降雨量不存在异常值。
3倍标准差找出异常值
根据正态分布的特性,在均值3倍标准差范围内的数据,包含约99.7%的数据。我们可以将3倍标准差范围以外的数据全部视为异常值。
参考:https://xxmdmst.blog.csdn.net/article/details/115410809#t15
例如查看GDP的异常值:
mean, std = data.GDP.mean(), data.GDP.std()
lower, upper = mean - 3 * std, mean + 3 * std
print(f"均值:{mean:.2f},标准差:{std:.2f},3倍标准差范围:({lower:.2f}, {upper:.2f})")
data.query("GDP < @lower | GDP > @upper").GDP
均值:2390.90,标准差:3254.88,3倍标准差范围:(-7373.73, 12155.53)
16 22968.60
63 18100.41
202 24964.99
207 17502.99
215 14504.07
230 16538.19
256 17900.00
314 15719.72
Name: GDP, dtype: float64
可以将其封装为一个方法:
def query_3std_outlier(data, column, gt_zero=True):
mean, std = data[column].mean(), data[column].std()
lower, upper = mean - 3 * std, mean + 3 * std
lower = 0 if gt_zero and lower < 0 else lower
print(f"均值:{mean:.2f},标准差:{std:.2f},3倍标准差范围:({round(lower,2)}, {upper:.2f})")
return data.query(f"{column} < @lower | {column} > @upper")[column]
查看人口密度的异常值:
query_3std_outlier(data, "PopulationDensity")
均值:2610.88,标准差:2910.68,3倍标准差范围:(0, 11342.92)
7 20547
66 11366
256 25900
312 15055
Name: PopulationDensity, dtype: int64
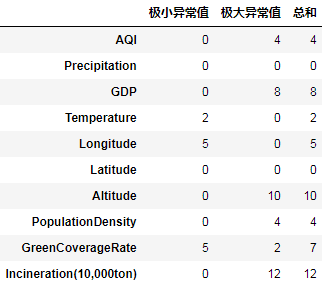
可以通过以下代码查看每个数值列基于3倍标准差的异常值个数:
def func(s):
mean, std = s.mean(), s.std()
lower, upper = mean - 3 * std, mean + 3 * std
a, b = (s < lower).sum(), (s > upper).sum()
return pd.Series((a, b, a+b), index=("极小异常值", "极大异常值", "总和"))
data.select_dtypes(include='number').agg(func).T
基于箱线图的规则找出异常值
箱线图判断异常值的标准是,四分位距IQR=Q3-Q1,上下边界:Q3+1.5IQR,Q1-1.5IQR。基于此编写方法:
def query_box_outlier(data, column, gt_zero=True):
q1, q3 = np.quantile(data[column], [0.25, 0.75])
IQR = q3-q1
lower, upper = q1 - 1.5 * IQR, q3 + 1.5 * IQR
lower = 0 if gt_zero and lower < 0 else lower
print(
f"Q1:{q1:.2f},Q3:{q3:.2f},IQR:{IQR:.2f},正常数据范围:({round(lower,2)}, {upper:.2f})")
print("异常值:", data.query(
f"{column} < @lower | {column} > @upper")[column].tolist())
例如查看GDP的箱线图异常值:
query_box_outlier(data, "GDP")
Q1:762.97,Q3:2735.34,IQR:1972.37,正常数据范围:(0, 5693.90)
异常值: [22968.6, 10912.17, 7700.0, 6275.06, 8003.92, 18100.41, 5751.2, 10053.58, 6130.68, 9720.77, 6148.4, 8011.5, 9300.07, 6137.74, 24964.99, 17502.99, 7280.0, 14504.07, 6225.3, 16538.19, 8518.26, 10905.06, 5810.03, 17900.0, 6446.08, 8510.13, 7315.19, 15719.72]
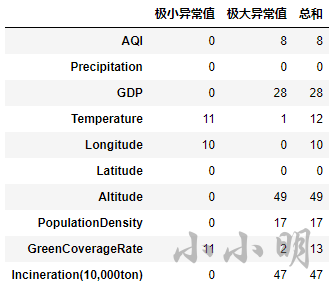
很明显按照箱线图的标准判断出的异常值比3倍标准差多很多。
下面按照箱线图的标准计算一下各列的异常值的数量:
def func(s):
q1, q3 = np.quantile(s, [0.25, 0.75])
IQR = q3-q1
lower, upper = q1 - 1.5 * IQR, q3 + 1.5 * IQR
a, b = (s < lower).sum(), (s > upper).sum()
return pd.Series((a, b, a+b), index=("极小异常值", "极大异常值", "总和"))
data.select_dtypes(include='number').agg(func).T
异常值处理的方式
异常值处理常见的处理方式有:删除异常数据、视为缺失值、对数转换、使用边界值替换、分箱离散化。本节不实际进行处理,简单演示下各种操作方法,后续再模型预测时,再测试各种方法处理异常值后的预测效果。
对数转换
由于右偏分布在取对数后,往往呈现正态分布,所以我们可以对右偏分布进行取对数转换。
例如,GDP变量呈现严重的右偏分布,看下对数转换前后的数据分布情况:
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
sns.histplot(data.GDP, stat="density", kde=True, ax=ax[0])
sns.histplot(np.log(data.GDP), stat="density", kde=True, ax=ax[1])
边界值替换
有基于正态分布3倍标准差和箱线图两种方式判断异常值,下面我们基于箱线图的标准进行边界值替换。
查看处理前的数据:
data.select_dtypes("number").agg(["max", "min"])
对所有列用边界值替换处理后再查看:
data_c = data.copy()
for c, s in data.select_dtypes("number").iteritems():
q1, q3 = np.quantile(s, [0.25, 0.75])
IQR = q3-q1
lower, upper = q1 - 1.5 * IQR, q3 + 1.5 * IQR
data_c[c] = s.clip(lower, upper)
data_c.select_dtypes("number").agg(["max", "min"]).round(2)
再次查看箱线图:
fig, ax = plt.subplots(2, 5)
# wspace左右距离,hspace上下距离
plt.subplots_adjust(wspace=0.05, hspace=0.5)
fig.set_size_inches(15, 3)
for i, c in enumerate(data.select_dtypes("number").columns):
row, col = i//5, i % 5
sns.boxplot(data=data_c, x=c, ax=ax[row, col])
可以看到,替换后箱线图已经不再有异常值。
分箱离散化
有时,特征对目标值的影响未必是线性的增加,而是阶梯式的影响,此时可以使用分箱方式,对特征进行离散化处理。
后面建模部分将使用KBinsDiscretizer一次性对多列分箱并编码。
重复值处理
# 发现重复值。
print(data.duplicated().sum())
# 查看哪些记录出现了重复值。
data[data.duplicated(keep=False)]
结果:
2
重复值需要进行去重仅保留一条:
data.drop_duplicates(inplace=True)
print(data.duplicated().sum())#去重后检查
结果:
0
数据分析
哪些城市的空气质量较好/较差?
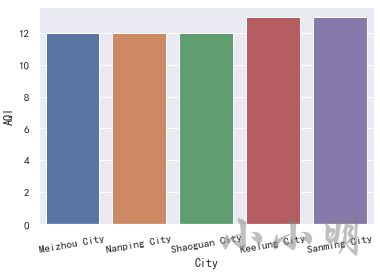
空气质量最好的5个城市
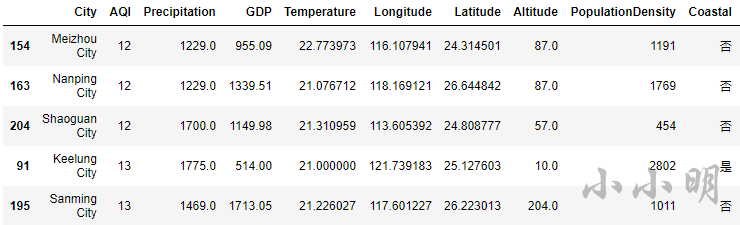
t = data.nsmallest(5, "AQI")
display(t)
plt.xticks(rotation=10)
sns.barplot(x="City", y="AQI", data=t)
可以看到,空气质量最好的5个城市为 梅州、南平、韶关、基隆、三明。
空气质量最差的5个城市
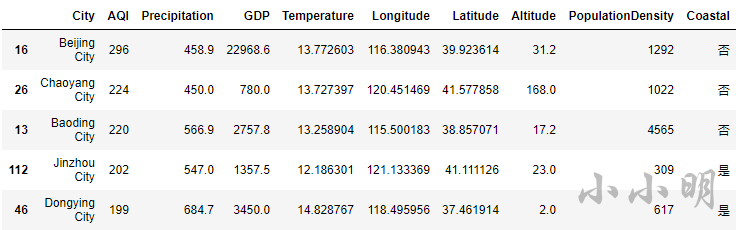
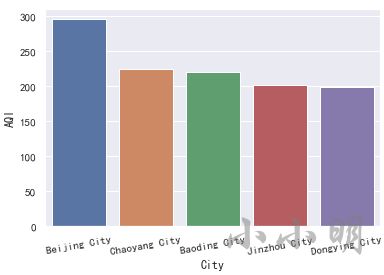
t = data.nlargest(5, "AQI")
display(t)
plt.xticks(rotation=10)
sns.barplot(x="City", y="AQI", data=t)
可以看到,空气质量最差的5个城市为 北京、朝阳、保定、锦州、东营。
全国城市的空气质量
城市空气质量的等级统计
空气质量指数的取值范围定为0~500,空气质量的等级划分标准为:
| AQI指数 | 等级 | 描述 |
|---|---|---|
| ≤50(0-50) | 一级 | 优 |
| ≤100(51-100) | 二级 | 良 |
| ≤150(101-150) | 三级 | 轻度污染 |
| ≤200(151-200) | 四级 | 中度污染 |
| ≤300(201-300) | 五级 | 重度污染 |
| >300(301-500) | 六级 | 严重污染 |
查看AQI的最大值:
data.AQI.max()
296
说明全国空气质量最差的城市没有达到严重污染的程度,后续分箱无需考虑严重污染。
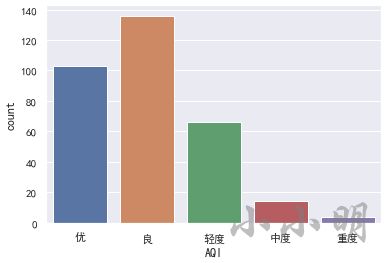
下面我们按照上述等级划分标准分箱,并统计全国空气质量每个等级的数量:
level = pd.cut(data.AQI, [0, 50, 100, 150, 200, 300],
labels=['优', '良', '轻度', '中度', '重度'])
display(level.value_counts(sort=False))
sns.countplot(x=level)
优 103
良 136
轻度 66
中度 14
重度 4
Name: AQI, dtype: int64
可以看到,各城市的空气质量以优与良为主,轻度污染占一部分,中度以上污染的城市占少数。
全国空气质量等级分布
下面我们绘制全国各城市空气质量等级分布图:
data["level"] = level
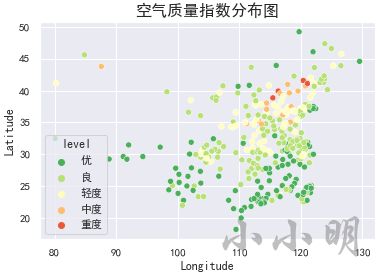
sns.scatterplot(x="Longitude", y="Latitude", hue="level",
palette="RdYlGn_r", data=data)
plt.title("空气质量等级分布图", size=16)
plt.show()
从上图大致的地理位置来看,西部城市整体上好于东部城市,南部城市普遍好于北部城市。
临海城市的空气质量是否优于内陆城市?
数量统计
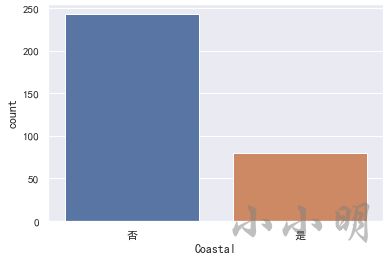
首先看下临海城市与内陆城市的数量:
print(data.Coastal.value_counts())
sns.countplot(x="Coastal", data=data)
否 243
是 80
Name: Coastal, dtype: int64
分布统计
Coastal的值为是表示沿海城市,否表示内陆城市。
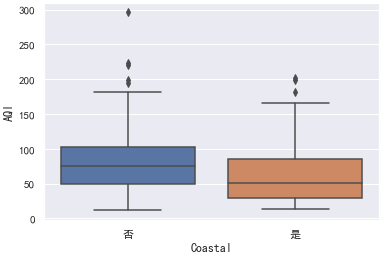
箱线图可以清楚看到均值、Q1分位点、Q3分位点以及临界值:
sns.boxplot(x="Coastal", y="AQI", data=data)
超过临界值,在1.5倍IQR之外的是异常值。
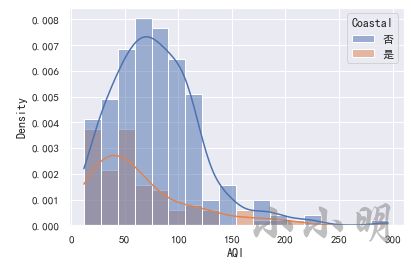
看分布密度,可以使用直方图:
sns.histplot(data, x="AQI", hue="Coastal", stat="density", kde=True)
小提琴图则能同时展示箱线图和分布的密度:
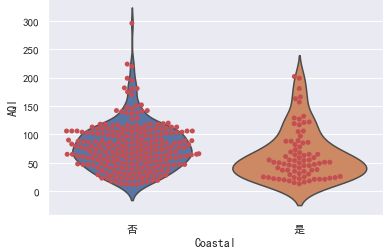
sns.violinplot(x="Coastal", y="AQI", data=data)
可以将小提琴图内部的箱线图替换为分簇散点图,可以更清晰观察数据分布情况:
sns.violinplot(x="Coastal", y="AQI", data=data, inner=None)
sns.swarmplot(x="Coastal", y="AQI", color="r", data=data)
根据中心极限定理,样本的均值有95%的概率会在1.96倍标准差以内,95%置信度的置信区间就是该范围。
参考:https://xxmdmst.blog.csdn.net/article/details/115410809#t16
基于此,我们可以假设样本符合正态分布计算均值和置信区间:
for x, aqi in data.AQI.groupby(data.Coastal):
x = "沿海" if x == "是" else "内陆"
mean, std = aqi.mean(), aqi.std()
se = std / np.sqrt(aqi.shape[0])
min_ = mean - 1.96 * se
max_ = mean + 1.96 * se
print(f"{x}95%置信度的置信区间为({min_:.2f},{max_:.2f}),均值为{mean:.2f}")
结果:
内陆95%置信度的置信区间为(69.91,88.18),均值为79.05
沿海95%置信度的置信区间为(54.17,73.96),均值为64.06
scipy提供了计算正态分布置信区间的方法:
from scipy import stats
for x, aqi in data.AQI.groupby(data.Coastal):
x = "沿海" if x == "是" else "内陆"
mean = aqi.mean()
min_, max_ = stats.norm.interval(0.95, mean, stats.sem(aqi))
print(f"{x}95%置信度的置信区间为({min_:.2f},{max_:.2f}),均值为{mean:.2f}")
不过实际上样本数量较少,相对正态分布而言样本更符合t分布,基于t分布计算置信区间:
for x, aqi in data.AQI.groupby(data.Coastal):
x = "沿海" if x == "是" else "内陆"
mean = aqi.mean()
min_, max_ = stats.t.interval(0.95, df=len(
aqi) - 1, loc=mean, scale=stats.sem(aqi))
print(f"{x}95%置信度的置信区间为({min_:.2f},{max_:.2f}),均值为{mean:.2f}")
内陆95%置信度的置信区间为(73.78,84.31),均值为79.05
沿海95%置信度的置信区间为(54.02,74.11),均值为64.06
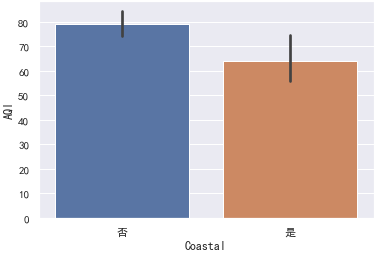
当然我们可以直接绘制柱形图展示均值和置信区间,无需自己计算:
sns.barplot(x="Coastal", y="AQI", data=data)
注:柱形图上方的竖线表示置信区间。
对于样本数据的各种分布统计图,都可以很明显的看到沿海城市的AQI整体上低于内陆城市,为了确凿的说明这个结论我们可以使用假设检验。
差异检验:两样本t检验
下面我们进行两样本t检验,检验沿海与内陆城市的AQI均值差异是否显著。
from scipy import stats
coastal = data.query("Coastal=='是'").AQI
inland = data.query("Coastal=='否'").AQI
进行两样本t检验前,需要先知道两样本的方差是否一致。所以首先进行方差齐性检验:
stats.levene(coastal, inland)
结果:
LeveneResult(statistic=0.08825036641952543, pvalue=0.7666054880248168)
方差齐性检验的原假设为方差相等(齐性),显然p-value超过显著性水平0.05,说明两样本的方差是相等的。
下面进行两样本t检验:
#equal_var=True表示两样本方差一致
r = stats.ttest_ind(coastal, inland, equal_var=True)
r
结果:
Ttest_indResult(statistic=-2.7303827520948905, pvalue=0.006675422541012958)
两样本t检验的原假设为均值相等,P值小于显著性水平,所以拒绝原假设,接受备择假设,即内陆AQI和沿海城市AQI的均值不相等。
由于统计量由左样本减右样本得到,统计量小于0说明 临海的均值小于内陆。
下面我们假设临海空气质量的均值小于内陆空气质量的均值,则这是一个右边假设检验,可以通过以下方法根据前面两样本t检验得到的统计量得到P值:
p = stats.t.sf(r.statistic, df=len(coastal)+len(inland)-2)
p
结果:
0.9966622887294936
说明有99.7%的信心可以认为沿海的空气质量整体好于内陆空气质量(均值小于内陆)。
关于t分布
设 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X \sim N(0,1), Y \sim \chi^{2}(n) X∼N(0,1),Y∼χ2(n),且 X , Y X, Y X,Y 相互独立 ,则称随机变量 t = X Y / n \Large{t=\frac{X}{\sqrt{Y / n}}} t=Y/nX服从自由度为 n 的 t 分布,记为 t ∼ t ( n ) \Large {t \sim t(n)} t∼t(n)
1908年英国统计学学者Gosset 以“Student” 为笔名发表了他的研究成果 ,其中引入了t 分布的概念 ,所以 t 分布被称为 Student t distribution 。
t分布的概率密度为:
t n ( x ) = Γ ( n + 1 2 ) n π Γ ( n 2 ) ( 1 + x 2 n ) − n + 1 2 ( − ∞ < x < + ∞ ) \Large{t_{n}(x)=\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n \pi }\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}}(-\infty
其中 Γ \Gamma Γ 是 Γ \Gamma Γ 函数: Γ ( s ) = ∫ 0 + ∞ e − x x s − 1 d x \Large {\Gamma(s)=\int_{0}^{+\infty} e^{-x} x^{s-1} d x} Γ(s)=∫0+∞e−xxs−1dx
或 Γ ( s ) = 2 ∫ 0 + ∞ e − x 2 x 2 s − 1 d x \Large {\Gamma(s)=2 \int_{0}^{+\infty} e^{-x^{2}} x^{2 s-1} d x} Γ(s)=2∫0+∞e−x2x2s−1dx
由于 t n ( x ) t_n(x) tn(x)是偶函数,其图形关于 y 轴对称,并且 E(X)=0 ( 若密度函数关于 x=c 对称 ,则 E(X)=c)
lim n → ∞ ( 1 + x 2 n ) − n + 1 2 = e lim n → ∞ x 2 n ( − n + 1 2 ) = e − x 2 2 \Large{\lim _{n \rightarrow \infty}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}}=e^{\lim_{n \rightarrow \infty} \frac{x^{2}}{n}\left(-\frac{n+1}{2}\right)}=e^{-\frac{x^{2}}{2}}} limn→∞(1+nx2)−2n+1=elimn→∞nx2(−2n+1)=e−2x2
lim n → ∞ t n ( x ) = 1 2 π e − x 2 2 = φ ( x ) \Large{\lim _{n \rightarrow \infty} t_{n}(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}}=\varphi(x)} limn→∞tn(x)=2π1e−2x2=φ(x)
系数必须趋于 1 2 π \frac{1}{\sqrt{2 \pi}} 2π1, 否则不是概率密度 。
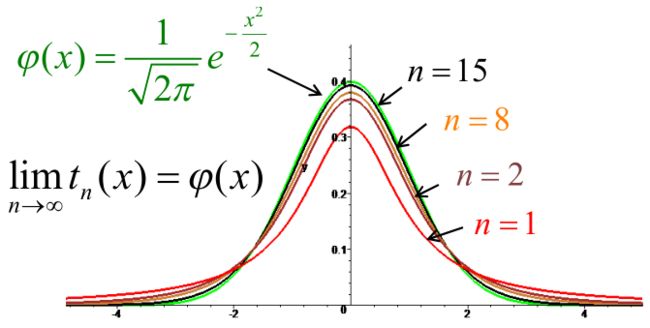
即 n 趋于无穷大时 ,t 分布以标准正态分布 N(0,1) 为极限分布 。
当 n 较小时,t 分布与N(0,1) 相差较大 。
t n ( x ) = Γ ( n + 1 2 ) n π Γ ( n 2 ) ( 1 + x 2 n ) − n + 1 2 \Large{t_{n}(x)=\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n \pi }\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}}} tn(x)=nπΓ(2n)Γ(2n+1)(1+nx2)−2n+1 的函数图像:
空气质量主要受哪些因素影响?
一般我们会有如下疑问:
- 人口密度大,是否会对空气质量造成负面影响?
- 绿化率高,是否能提高空气质量?
多图矩阵
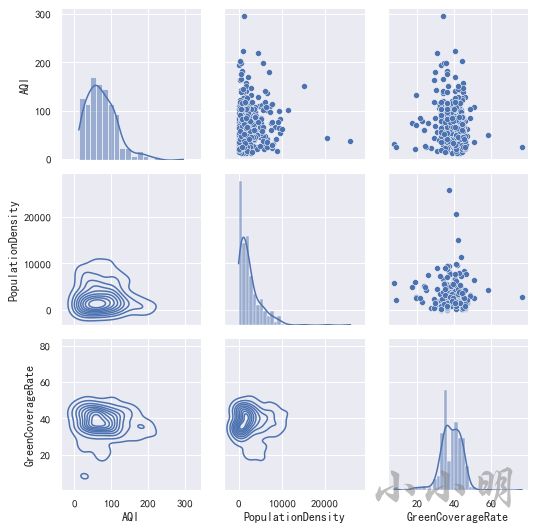
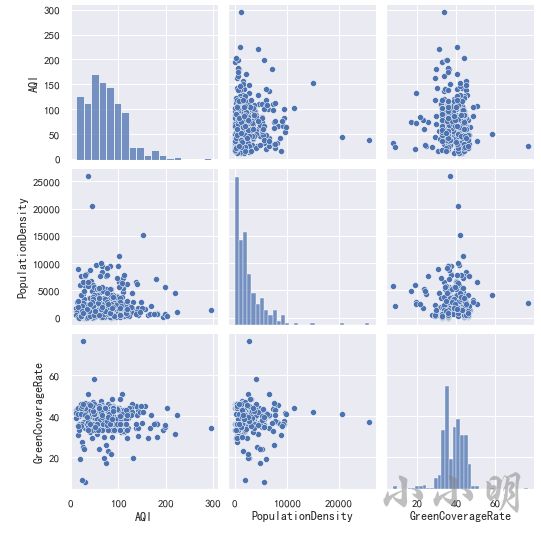
首先查看空气质量、人口密度和绿化率之间的矩阵图:
g = sns.PairGrid(data[["AQI", "PopulationDensity", "GreenCoverageRate"]])
g.map_upper(sns.scatterplot)
g.map_lower(sns.kdeplot)
g.map_diag(sns.histplot, kde=True)
也可以直接绘制散点图矩阵:
#参数 kind="reg"给散点图绘制一条回归线
sns.pairplot(data[["AQI", "PopulationDensity", "GreenCoverageRate"]])
从散点图矩阵中可以看到,三个变量两两之间并没有明显的线性关系,可以说几乎不相关。
相关系数
变量X与变量Y的协方差定义为:
Cov ( X , Y ) = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) n − 1 \large{\operatorname{Cov}(X, Y)=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{n-1}} Cov(X,Y)=n−1∑i=1n(xi−xˉ)(yi−yˉ)
x ˉ \bar{x} xˉ表示变量X的均值。
协方差体现两个变量之间的分散性以及两个变量变化步调是否一致。当协方差的两个变量相同时,协方差就是方差。
相关系数的定义:
r ( X , Y ) = Cov ( X , Y ) σ X σ Y \large{r(X, Y)=\frac{\operatorname{Cov}(X, Y)}{\sigma_{X} \sigma_{Y}}} r(X,Y)=σXσYCov(X,Y)
= ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 \large{=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}} =∑i=1n(xi−xˉ)2∑i=1n(yi−yˉ)2∑i=1n(xi−xˉ)(yi−yˉ)
σ X \sigma_{X} σX表示变量X的标准差。
相关系数的绝对值的取值范围是[0,1],可以根据相关系数衡量两个变量的相关性,正数代表正相关,负数代码负相关。绝对值的大小体现相关的程度:
-
0.8-1:极强相关
-
0.6-0.8:强相关
-
0.4-0.6:中等程度相关
-
0.2-0.4:弱相关
-
0-0.2:极弱相关或无相关
例如,计算空气质量与降雨量的相关系数:
x = data.AQI
y = data.Precipitation
# 计算AQI与Precipitation的协方差。
a = (x - x.mean()) * (y - y.mean())
cov = np.sum(a) / (len(a) - 1)
print("协方差:", cov)
# 计算AQI与Precipitation的相关系数。
corr = cov / np.sqrt(x.var() * y.var())
print("相关系数:", corr)
结果:
协方差: -10098.209013903044
相关系数: -0.40184407003013883
可以使用内置方法计算:
print("协方差:", x.cov(y))
print("相关系数:", x.corr(y))
结果:
协方差: -10098.209013903042
相关系数: -0.4018440700301393
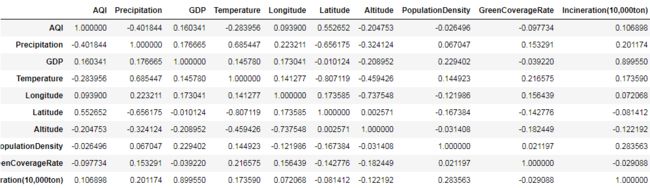
计算DataFrame中的所有数值列之间的相关系数:
data.corr()
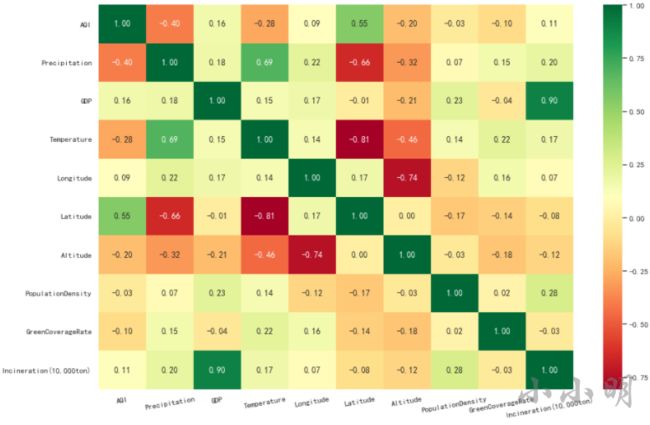
使用热力图呈现相关系数更佳:
plt.figure(figsize=(15, 10))
ax = sns.heatmap(data.corr(), cmap="RdYlGn", annot=True, fmt=".2f")
plt.xticks(rotation=10)
plt.show()
从上述相关性热力图中,我们可以看到,AQI与人口密度和绿化覆盖率几乎不相关。
AQI与纬度(0.55)和降雨量(-0.4)的相关性最高。说明:
- 纬度越低,空气质量越好。
- 降雨量越多,空气质量越好。
注:越往南方纬度越低,赤道的纬度是0。
此外,我们还可以发现一些其他的细节:
- GDP与焚烧量正相关,相关系数0.9。
- 温度与降雨量正相关,相关系数0.69。
- 纬度与温度负相关,相关系数-0.81,即南方城市普遍比北方城市温度高。
- 经度与海拔负相关,相关系数-0.74,即西部城市普遍比东部城市海拔高。
- 纬度与降雨量负相关,相关系数-0.66,即南方城市普遍比北方城市降雨多。
空气质量指数均值的验证
传言说,全国所有城市的空气质量指数均值为71左右,请问,这个消息可靠吗?
下面作出原假设:全部城市的AQI均值为71,进行假设检验:
print("样本均值 :", data.AQI.mean())
print(stats.ttest_1samp(data.AQI, 71))
结果:
样本均值 : 75.3343653250774
Ttest_1sampResult(statistic=1.8117630617496872, pvalue=0.07095431526986647)
可以看到,P值大于显著性水平0.05,故我们没有充足的证据拒绝原假设,于是接受原假设全部城市的AQI均值为71。
下面计算一下置信区间:
stats.t.interval(0.95, df=len(data) - 1, loc=data.AQI.mean(), scale=stats.sem(data.AQI))
结果: (70.6277615675309, 80.0409690826239)
因此,我们可以认为全国所有城市的平均空气质量,95%的可能在(70.63, 80.04)范围内。
对空气质量进行预测
问题:已知某市的降雨量、温度、经纬度等指标,如何预测其空气质量?
数据转换
为了进行模型计算,我们首先需要将一些文本型变量转换为离散数值变量。
data.Coastal = data.Coastal.map({"是": 1, "否": 0})
data.Coastal.value_counts()
0 243
1 80
Name: Coastal, dtype: int64
注意:只有两个类别时,转换为任意两个数值都可以。如果存在三个以上的分类,一般情况下应使用独热编码(例如pd.get_dummies)对变量进行转换,因为一般情况下三个类别之间并不存在线性关系。
基础模型
首先建立一个基本的线性回归模型,后续操作在此基础上改进:
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 特征数据后续要进行异常数据替换,所以保留列信息
X = data.drop(["City", "AQI", "level"], axis=1)
y = data.AQI.values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
lr = LinearRegression()
lr.fit(X_train, y_train)
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))
结果:
0.4538897765064037
0.4040770562383651
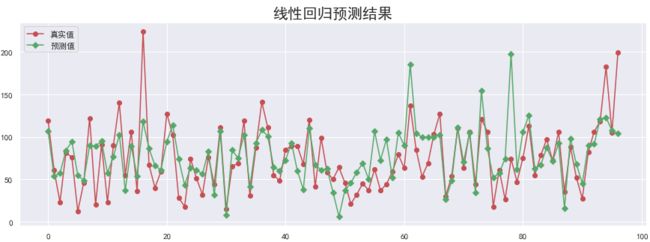
真实值与预测值对比图:
y_hat = lr.predict(X_test)
plt.figure(figsize=(15, 5))
plt.plot(y_test, "-r", label="真实值", marker="o")
plt.plot(y_hat, "-g", label="预测值", marker="D")
plt.legend(loc="upper left")
plt.title("线性回归预测结果", fontsize=20)
plt.show()
下面我们将尝试优化模型提高模型效果。
临界值替换异常值
数据中存在异常值,可能影响模型的效果,我使用前面在异常值处理一节中使用的方法对异常值进行临界值替换。
首先我们使用训练集的临界值替换异常值:
for c in X_train.columns.drop("Coastal"):
s = X_train[c]
q1, q3 = np.quantile(s, [0.25, 0.75])
IQR = q3-q1
lower, upper = q1 - 1.5 * IQR, q3 + 1.5 * IQR
s.clip(lower, upper, inplace=True)
X_test[c].clip(lower, upper, inplace=True)
注意:测试集应视为未知数据,所以我们只能使用训练集的数据计算临界值,再对训练集和测试集中的异常值进行替换。
再次查看模型效果:
lr.fit(X_train, y_train)
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))
结果:
0.4631142291492417
0.44614202658395546
可以看到模型相对之前有轻微的改进。
特征选择
前面我们使用了全部的特征进行训练,但实际上特征并非越多越好,有些特征对模型质量几乎没有改善,应该删除提高模型的训练速度。
下面我们使用RFECV来实现特征选择,RFECV分为两部分:
- RFE(Recursive feature elimination) :递归特征消除,用来对重要的特征进行评级。
- CV(Cross Validation) :交叉验证,在特征评级后,通过交叉验证,选择最佳数量的特征。
具体过程如下:
- RFE阶段。
- 初始的特征集为所有可用的特征。
- 使用当前特征集进行建模,然后计算每个特征的重要性。
- 删除最不重要的一个(或多个)特征,更新特征集。
- 跳转到步骤2,直到完成所有特征的重要性评级。
- CV阶段。
- 根据RFE阶段确定的特征重要性,依次选择不同数量的特征。
- 对选定的特征集进行交叉验证。
- 确定平均分最高的特征数量,完成特征选择。
下面开始进行递归特征消除,并进行交叉验证:
from sklearn.feature_selection import RFECV
# estimator: 要操作的模型。
# step: 每次删除的变量数。
# cv: 使用的交叉验证折数。
# n_jobs: 并发的数量。
# scoring: 评估的方式。
rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2")
rfecv.fit(X_train, y_train)
print("剩余的特征数量:", rfecv.n_features_)
# 返回经过特征选择后,使用缩减特征训练后的模型。
print(rfecv.estimator_)
# 返回每个特征的等级,数值越小,特征越重要。
print(rfecv.ranking_)
print("被选择的特征布尔数组:", rfecv.support_)
mean_test_score = rfecv.cv_results_["mean_test_score"]
print("交叉验证的评分:", mean_test_score)
结果:
剩余的特征数量: 9
LinearRegression()
[1 1 1 1 1 1 2 1 1 1]
被选择的特征布尔数组: [ True True True True True True False True True True]
交叉验证的评分: [-0.06091362 0.1397744 0.19933237 0.16183209 0.18281661 0.20636585
0.29772708 0.307344 0.30877162 0.30022701]
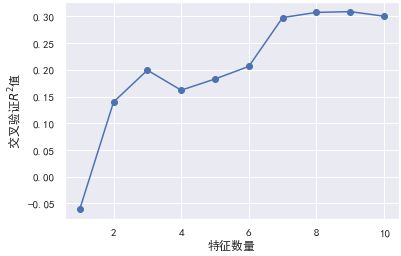
绘图表示,在特征选择的过程中,使用交叉验证获取R平方的值:
plt.plot(range(1, len(mean_test_score) + 1), mean_test_score, marker="o")
plt.xlabel("特征数量")
plt.ylabel("交叉验证$R^2$值")
从图中可以看到,9个特征时模型可以达到最佳的效果。那么我们可以删除该特征。
先看看被删除的特征列:
del_cols = X_train.columns[~rfecv.support_].values
print("剔除的变量:", del_cols)
剔除的变量: ['PopulationDensity']
然后看看删除该特征后,模型的评分:
X_train_eli = X_train.drop(columns=del_cols)
X_test_eli = X_test.drop(columns=del_cols)
print(rfecv.estimator_.score(X_train_eli.values, y_train))
print(rfecv.estimator_.score(X_test_eli.values, y_test))
结果:
0.46306656191488604
0.44502255894082043
从结果可以看到,剔除该特征后,模型的评分几乎不变化(下降0.1%左右)。
分箱离散化
由于有些变量对目标的影响并不是连续的,而是阶梯式的,所以我们可以考虑使用KBinsDiscretizer对有这种特征的数据作分箱离散化。
KBinsDiscretizer是K个分箱的离散器,用于将数值(通常是连续变量)变量进行区间离散化操作。
KBinsDiscretizer的参数如下:
- n_bins:分箱(区间)的个数。
- encode:离散化编码方式。分为:onehot,onehot-dense与ordinal。
- onehot:使用独热编码,返回稀疏矩阵。
- onehot-dense:使用独热编码,返回稠密矩阵。
- ordinal:使用序数编码(0,1,2……)。
- strategy:分箱的方式。分为:uniform,quantile,kmeans。
- uniform:每个区间的长度范围大致相同。
- quantile:每个区间包含的元素个数大致相同。
- kmeans:使用一维kmeans方式进行分箱。
下面我对经度,纬度,温度 和 降雨量 进行分箱离散化,读者们可以自己凭感觉测试其他的参数。
from sklearn.preprocessing import KBinsDiscretizer
k = KBinsDiscretizer(n_bins=[4, 6, 5, 14],
encode="onehot-dense", strategy="uniform")
# 经纬度,温度,降雨量
discretize = ["Longitude", "Latitude", "Temperature", "Precipitation"]
# 将目标特征进行分箱李四化
X_train_dis = k.fit_transform(X_train_eli[discretize])
print(X_train_dis.shape[1])
# 将剔除离散化特征的其他特征与离散化后的特征进行重新组合
X_train_dis = np.c_[X_train_eli.drop(columns=discretize).values, X_train_dis]
# 对测试集进行同样的离散化操作。
X_test_dis = k.transform(X_test_eli[discretize])
X_test_dis = np.c_[X_test_eli.drop(discretize, axis=1).values, X_test_dis]
29
上面的代码将经度、维度、温度和降雨量分别拆分成4、6、5、14个区间,使用独热编码意味着每个区间都会成为单独的一列,所以总共有29列。
然后我们对转换后的数据进行训练:
lr.fit(X_train_dis, y_train)
print(lr.score(X_train_dis, y_train))
print(lr.score(X_test_dis, y_test))
0.6892388692774563
0.654606234835567
可以看到模型在经过分箱离散化操作后,预测效果大幅度提高。
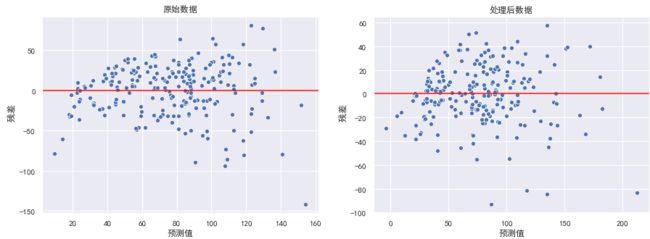
残差图分析
残差就是模型的预测值与真实值之间的差异,可以绘制残差图对模型进行评估,横坐标为预测值,纵坐标为真实值。
对于一个模型,误差应该的随机性的,而不是有规律的。残差也随机分布于中心线附近,如果残差图中残差是有规律的,则说明模型遗漏了某些能够影响残差的解释信息。
异方差性,是指残差具有明显的方差不一致性。
绘制残差图:
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
data = [X_train, X_train_dis]
title = ["原始数据", "处理后数据"]
for d, a, t in zip(data, ax, title):
model = LinearRegression()
model.fit(d, y_train)
y_hat_train = model.predict(d)
residual = y_hat_train - y_train
a.set_xlabel("预测值")
a.set_ylabel(" 残差")
a.axhline(y=0, color="red")
a.set_title(t)
sns.scatterplot(x=y_hat_train, y=residual, ax=a)
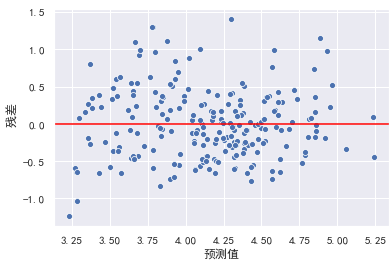
在左图中,可以看出随着预测值的增大,残差也有增大的趋势。此时我们可以使用对y值取对数的方式处理。
model = LinearRegression()
y_train_log = np.log(y_train)
y_test_log = np.log(y_test)
model.fit(X_train, y_train_log)
y_hat_train = model.predict(X_train)
residual = y_hat_train - y_train_log
plt.xlabel("预测值")
plt.ylabel(" 残差")
plt.axhline(y=0, color="red")
sns.scatterplot(x=y_hat_train, y=residual)
此时异方差性得到解决,模型效果也可能会得到进一步提升。
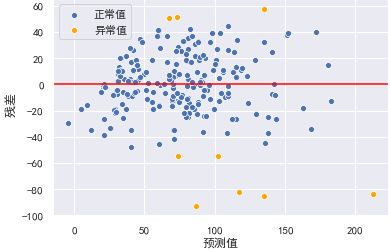
检查离群点:对于多元线性回归,其回归线已经成为超平面,无法通过可视化来观测。但我们可以通过残差图,通过预测值与实际值之间的关系,来检测离群点。我们认为偏离2倍标准差的点为离群点:
y_hat_train = lr.predict(X_train_dis)
residual = y_hat_train - y_train.values
r = (residual - residual.mean()) / residual.std()
plt.xlabel("预测值")
plt.ylabel(" 残差")
plt.axhline(y=0, color="red")
sns.scatterplot(x=y_hat_train[np.abs(r) <= 2],
y=residual[np.abs(r) <= 2], color="b", label="正常值")
sns.scatterplot(x=y_hat_train[np.abs(r) > 2], y=residual[np.abs(r) > 2], color="orange", label="异常值")
结果:
剔除异常值后,训练模型并查看效果:
X_train_dis_filter = X_train_dis[np.abs(r) <= 2]
y_train_filter = y_train[np.abs(r) <= 2]
lr.fit(X_train_dis_filter, y_train_filter)
print(lr.score(X_train_dis_filter, y_train_filter))
print(lr.score(X_test_dis, y_test))
结果:
0.7354141753913532
0.6302724058812207
可以看到在剔除残差的标准差超过2倍的数据后,模型效果得到了进一步的提升。
结论
- 2015年空气质量最好的5个城市为 梅州、南平、韶关、基隆、三明。
- 2015年空气质量最差的5个城市为 北京、朝阳、保定、锦州、东营。
- 2015年各城市的空气质量以优与良为主,轻度污染占一部分,中度以上污染的城市占少数。
- 总体上,西部城市好于东部城市,南部城市好于北部城市。
- 是否临海,降雨量与纬度对空气质量的影响较大。
- 我国城市平均空气质量指数大致在(70.63~80.04)这个区间内,该区间的可能性概率为95%。