时序 transformer

时列 transformer

介绍

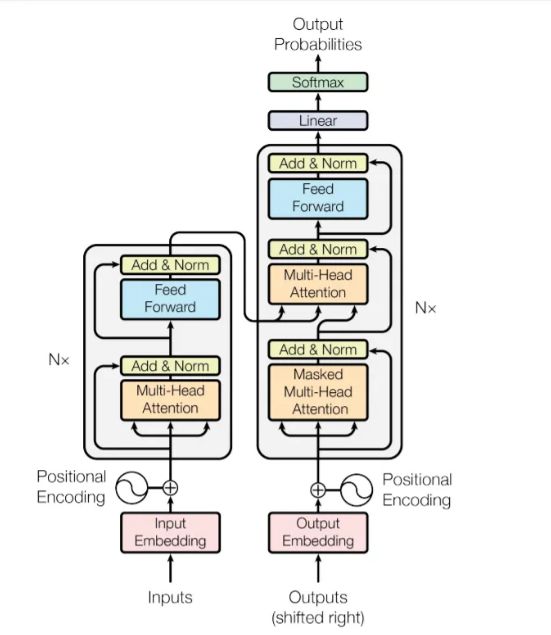
Attention Is All You Need 中提到。它是更健壮的卷积吗？ 从更少的参数中挤出更多的学习能力仅仅是一种黑客手段吗？ 它应该稀疏吗？ 原始作者是如何提出这种架构的？

• 它比RNN更好，因为它不会重复出现，并且可以使用先前的时步功能而不会造成细节损失
• 它是多种任务中性能最高的体系结构，包括但不限于：NLP，视觉，回归（可扩展）

从现有的RNN模型切换到Attention体系结构非常容易。 输入的形状相同！

预处理

在时间序列任务中使用 transformer 与在NLP或计算机视觉中使用 transformer 是不同的。我们既不标记数据，也不将它们切割成16x16的图像块。相反，我们遵循一种更为经典/老派的方法来准备训练数据。

有一点是绝对正确的，那就是我们必须把数据输入到与输入相同的值范围内，以消除偏差。这通常在[0，1]或[-1，1]范围内。通常，建议对所有输入特性应用相同的预处理管道，以消除这种偏差。个别用例可能不受此限制，不同的模型和数据是唯一的！考虑一下数据的来源。

流行的时间序列预处理技术包括：

• 只需缩放为[0，1]或[-1，1]
• 标准缩放比例（去除均值，除以标准偏差）
• 幂变换（使用幂函数将数据推入更正态分布，通常用于偏斜数据/存在异常值的情况）
• 离群值去除
• 成对差异或计算百分比差异
• 季节性分解（试图使时间序列固定）
• 工程化更多特征（自动特征提取器，存储到百分位数等）
• 在时间维度上重采样
• 在要素维度中重新采样（而不是使用时间间隔，而对要素使用谓词来重新安排时间步长（例如，当记录的数量超过N个单位时）
• 滚动值
• 集合体
• 这些技术的结合

同样，预处理决策与问题和手头的数据紧密相关，但这是一个很好的入门清单。

如果您的时间序列可以通过进行季节性分解等预处理而变得平稳，则可以使用较小的模型（例如 ）（通过更快速的训练并且所需的代码和工作量更少）来获得良好的质量预测 NeuralProphet 或 Tensorflow Probability 。

深度神经网络可以在训练期间自行学习线性和周期性分量（我们将在以后使用Time 2 Vec）。 就是说，我建议不要将季节性分解作为预处理步骤。

其他决策（例如计算聚合和成对差异）取决于数据的性质以及您要预测的内容。

将序列长度视为一个超参数，这导致我们得到类似于RNN的输入张量形状： (batch size, sequence length, features)。

这是设置为3的所有尺寸的图形。

可学习的时间表示 time2vextor

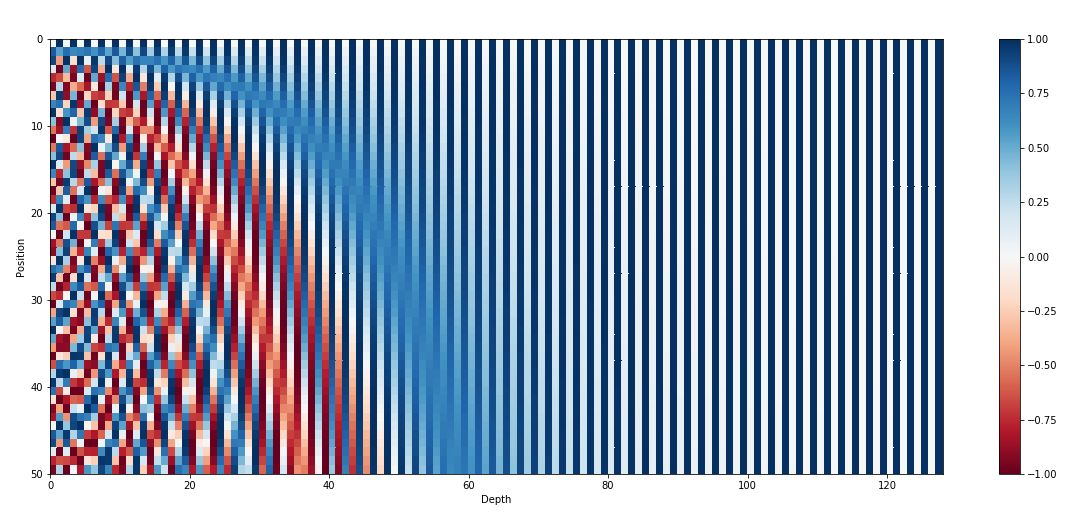
为了使工作正常，您需要在输入要素上附加时间的含义。 在原始的NLP模型中，将叠加的正弦函数集合添加到每个输入嵌入中。 现在我们需要一个不同的表示形式，因为我们的输入是标量值，而不是不同的单词/标记。

Positional Encoding Visualization from kazemnejad’s blog.

The Time 2 Vec paper 派上用场了。 这是一种可学习且互补的，与模型无关的时间重置。 如果您过去曾经学习过傅立叶变换，这应该很容易理解。

只需将每个输入要素分解为线性分量（line）和所需的多个周期性（正弦）分量即可。 通过将分解定义为函数，我们可以使权重通过反向传播来学习。

Time 2 Vec Decomposition Equation

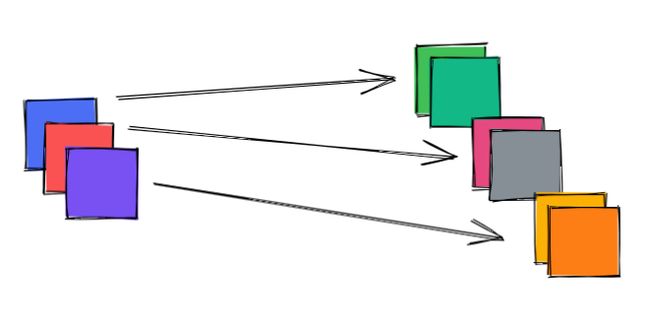
对于每个输入要素，我们以时间独立（时间分布层）的方式应用同一层。 这种可学习的嵌入与时间无关！ 最后，连接原始输入。

这是 的学习时间嵌入的示意图，它们 不同 每个输入要素类别（每个要素1个学习的线性分量和1个学习的周期性分量） 。

这并不意味着每个时间步都将具有相同的嵌入值，因为time2vec嵌入的计算取决于输入值！

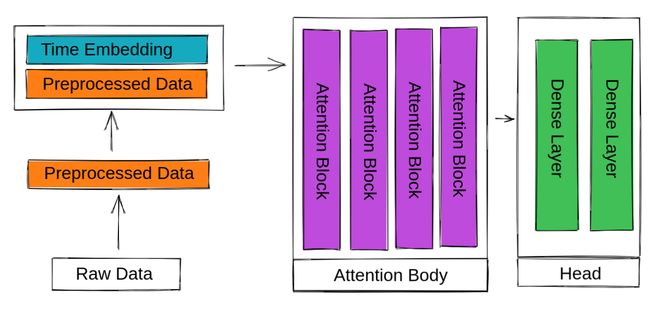
最后，我们将所有这些连接在一起以形成注意模块的输入。

class Time2Vec(keras.layers.Layer):
    def __init__(self, kernel_size=1):
        super(Time2Vec, self).__init__(trainable=True, name='Time2VecLayer')
        self.k = kernel_size
    
    def build(self, input_shape):
        # trend
        self.wb = self.add_weight(name='wb',shape=(input_shape[1],),initializer='uniform',trainable=True)
        self.bb = self.add_weight(name='bb',shape=(input_shape[1],),initializer='uniform',trainable=True)
        # periodic
        self.wa = self.add_weight(name='wa',shape=(1, input_shape[1], self.k),initializer='uniform',trainable=True)
        self.ba = self.add_weight(name='ba',shape=(1, input_shape[1], self.k),initializer='uniform',trainable=True)
        super(Time2Vec, self).build(input_shape)
    
    def call(self, inputs, **kwargs):
        bias = self.wb * inputs + self.bb
        dp = K.dot(inputs, self.wa) + self.ba
        wgts = K.sin(dp) # or K.cos(.)

        ret = K.concatenate([K.expand_dims(bias, -1), wgts], -1)
        ret = K.reshape(ret, (-1, inputs.shape[1]*(self.k+1)))
        return ret
    
    def compute_output_shape(self, input_shape):
        return (input_shape[0], input_shape[1]*(self.k + 1))

构建模型

我们将使用多头自我注意（将Q，K和V设置为取决于通过不同密集层/矩阵的输入）。 下一部分是可选的，取决于模型和数据的规模，但我们还将完全放弃解码器部分。 这意味着，我们将只使用一个或多个注意力障碍层。

在最后一部分中，我们将使用几个（一个或多个）密集层来预测我们想要预测的内容。

每个注意块均包括自我注意，层规范化和前馈—转发块。 每个块的输入尺寸等于其输出尺寸。

from tensorflow_addons.layers import MultiHeadAttention

class AttentionBlock(keras.Model):
    def __init__(self, name='AttentionBlock', num_heads=2, head_size=128, ff_dim=None, dropout=0, **kwargs):
        super().__init__(name=name, **kwargs)

        if ff_dim is None:
            ff_dim = head_size

        self.attention = MultiHeadAttention(num_heads=num_heads, head_size=head_size, dropout=dropout)
        self.attention_dropout = keras.layers.Dropout(dropout)
        self.attention_norm = keras.layers.LayerNormalization(epsilon=1e-6)

        self.ff_conv1 = keras.layers.Conv1D(filters=ff_dim, kernel_size=1, activation='relu')
        # self.ff_conv2 at build()
        self.ff_dropout = keras.layers.Dropout(dropout)
        self.ff_norm = keras.layers.LayerNormalization(epsilon=1e-6)

    def build(self, input_shape):
        self.ff_conv2 = keras.layers.Conv1D(filters=input_shape[-1], kernel_size=1) 

    def call(self, inputs):
        x = self.attention([inputs, inputs])
        x = self.attention_dropout(x)
        x = self.attention_norm(inputs + x)

        x = self.ff_conv1(x)
        x = self.ff_conv2(x)
        x = self.ff_dropout(x)

        x = self.ff_norm(inputs + x)
        return x

class ModelTrunk(keras.Model):
      def __init__(self, name='ModelTrunk', time2vec_dim=1, num_heads=2, head_size=128, ff_dim=None, num_layers=1, dropout=0, **kwargs):
        super().__init__(name=name, **kwargs)
        self.time2vec = Time2Vec(kernel_size=time2vec_dim)
        if ff_dim is None:
            ff_dim = head_size
        self.dropout = dropout
        self.attention_layers = [AttentionBlock(num_heads=num_heads, head_size=head_size, ff_dim=ff_dim, dropout=dropout) for _ in range(num_layers)]

        
    def call(self, inputs):
        time_embedding = keras.layers.TimeDistributed(self.time2vec)(inputs)
        x = K.concatenate([inputs, time_embedding], -1)
        for attention_layer in self.attention_layers:
            x = attention_layer(x)

        return K.reshape(x, (-1, x.shape[1] * x.shape[2])) # flat vector of features out

（可选）在头部之前，您可以应用某种类型的合并（例如，全局平均1D）。

技巧包（训练 transformer 注意事项）

使用“Transformers and Attention”以充分利用模型时需要考虑的事项。

• 从小开始

不要为超参数而疯狂。 从一个单一的，谦虚的注意力层，几个头部和低尺寸开始。 观察结果并相应调整超参数-不要过大！ 缩放模型以及数据。 但是，没有什么可以阻止您计划庞大的超参数搜索工作:)。

• 学习率热身

导致更大稳定性的注意力机制的关键部分是学习率预热。 从一个小的学习率开始，然后逐渐提高直到达到基数，然后再次降低。 您可能会因指数式的疯狂而烦恼-不断衰减的时间表和复杂的公式，但是我仅举一个简单的示例，您只需大声阅读以下代码就可以理解：

def lr_scheduler(epoch, lr, warmup_epochs=15, decay_epochs=100, initial_lr=1e-6, base_lr=1e-3, min_lr=5e-5):
    if epoch <= warmup_epochs:
        pct = epoch / warmup_epochs
        return ((base_lr - initial_lr) * pct) + initial_lr

    if epoch > warmup_epochs and epoch < warmup_epochs+decay_epochs:
        pct = 1 - ((epoch - warmup_epochs) / decay_epochs)
        return ((base_lr - min_lr) * pct) + min_lr

    return min_lr

callbacks += [keras.callbacks.LearningRateScheduler(partial(lr_scheduler, ...), verbose=0)]

• Use Adam (or variants)

非加速梯度下降优化方法不适用于Transformers。 Adam 是进行训练的最佳初始优化器选择。 请密切注意更新（可能更好）的优化技术，例如AdamW或NovoGrad！

references

The Time Series Transformer

[1] Attention Is All You Need, Ashish Vaswani and Noam Shazeer and Niki Parmar and Jakob Uszkoreit and Llion Jones and Aidan N. Gomez and Lukasz Kaiser and Illia Polosukhin, 2017

eries-transformer-2a521a0efad3)

[1] Attention Is All You Need, Ashish Vaswani and Noam Shazeer and Niki Parmar and Jakob Uszkoreit and Llion Jones and Aidan N. Gomez and Lukasz Kaiser and Illia Polosukhin, 2017

[2] Time2Vec: Learning a Vector Representation of Time, Seyed Mehran Kazemi and Rishab Goel and Sepehr Eghbali and Janahan Ramanan and Jaspreet Sahota and Sanjay Thakur and Stella Wu and Cathal Smyth and Pascal Poupart and Marcus Brubaker, 2019