Pytorch笔记：线性回归、softmax回归

1 线性回归

        线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。

1.1 线性模型

        首先我们建立一个模型，这个模型是房价预测模型，以此模型简单介绍线性回归模型。

        一般的线性模型如下所示：

        网络结构：

                 

  

 1.2 数据集

 1.3 损失函数

         损失函数（loss function）或代价函数（cost function）是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。在应用中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。对于这个模型，我们主要是采用了平方函数作为损失函数。

        选用平方损失的原因如下：
        假设数据满足高斯分布的情况下，将y = wx+b 中的y和期望带入高斯分布函数，取对数化简后为 常数-（平方损失函数/方差），是近似平方损失的函数且方差随数据变化是个定值。固定X使得W为参数时的似然估计最优解得到的概率，等同于真实W下的概率。所以最大化似然函数值转换为最小化平方损失函数。所以线性回归实质是寻找一组最接近的权值，也就是最大化似然函数值。平方损失函数，是最大化函数值的一个简便的式子。

1.4 优化方法

        1.4.1 梯度下降

        梯度的方向实际就是函数在此点上升最快的方向！而我们需要得到最小的损失，因此要朝着下降最快的方向走，也就是负的梯度方向，因此称为梯度下降。

        1.4.2 小批量随机梯度下降（mini-batch stochastic gradient descent）

        为了计算一次梯度需要遍历所有数据，数据集太大时花费巨大，因此便有了小批量随机梯度下降。

        对于MBGD的优点就显而易见了，每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。

        1.4.3 总结

        ① 梯度下降通过不断沿着梯度下降的方向更新参数求解；
        ② 小批量随机梯度下降是深度学习默认的求解算法；
        ③ 两个重要的超参数是批量大小和超参数。

1.5 算法实现

import random
import torch
from d2l import torch as d2l
 
 
# ***************************************** 构造数据集 ***************************************
def synthetic_data(w, b, num_examples):
    """生成y=wx+b+噪声的数据集"""
    x = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(x, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return x, y.reshape((-1, 1))
 
 
# **************************************** 读取数据集 *******************************************
def data_iter(batch_size, features, labels):
    num_example = len(features)
    indices = list(range(num_example))
    random.shuffle(indices)   # 打乱顺序，随机读取
    for i in range(0, num_example, batch_size):
        batch_indices = torch.tensor(indices[i:min(i + batch_size, num_example)])
        yield features[batch_indices], labels[batch_indices]
 
 
# *************************************** 初始化模型参数 *********************************************
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
 
 
# *************************************** 定义模型 ***************************************************
def linreg(x, w, b):
    return torch.matmul(x, w) + b       # 线性回归模型
 
 
# *************************************** 定义损失 ***************************************************
def squared_loss(y_hat, y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2  # 均方损失
 
 
# *************************************** 定义优化算法 ************************************************
def sgd(params, lr, batch_size):
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()
 
 
# *************************************** 训练 *******************************************************
def train():
    true_w = torch.tensor([2, -3.4])
    true_b = 4.2
    features, labels = synthetic_data(true_w, true_b, 1000)
 
    batch_size = 10
    lr = 0.03
    num_epochs = 3
    net = linreg
    loss = squared_loss
    for epoch in range(num_epochs):
        for x, y in data_iter(batch_size, features, labels):
            l = loss(net(x, w, b), y)        # 计算小批量损失
            l.sum().backward()                           # 对小批量损失求和
            sgd([w, b], lr, batch_size)                  # 更新梯度
        with torch.no_grad():   # 在该模块下，所有计算得出的tensor的requires_grad都自动设置为False，可以节约内存
            train_l = loss(net(features, w, b), labels)
            print(f'epoch{epoch + 1}, loss{float(train_l.mean()):f}')
 
    print(f'w的估计误差：{true_w - w.reshape(true_w.shape)}')
    print(f'b的估计误差：{true_b - b}')
 
 
if __name__ == "__main__":
    train()

运行结果：

PS E:\pytorch> & E:/Python/python.exe e:/pytorch/linear.py
epoch1, loss0.056585
epoch2, loss0.000264
epoch3, loss0.000052
epoch4, loss0.000051
w的估计误差：tensor([-0.0004, -0.0002], grad_fn=)
b的估计误差：tensor([0.0006], grad_fn=)

2 softmax与分类问题

 2.1 回归与分类

        回归可以看作是对单分类的预测。

2.2 softmax

         softmax回归是一个单层神经网络，softmax回归的输出层是一个全连接层，网络结构如下图所示。

              

2.3 softmax运算

        softmax运算可以解决以下两个问题：

        1.输出层的输出值的范围不稳定，我们难以直观上判断这些值的意义。

        2.真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量

        尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。因此，softmax回归是一个线性模型。

2.4 损失函数 

        交叉熵损失函数：

 2.5 代码实现

import matplotlib
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
from IPython import display
matplotlib.use("Tkagg")
d2l.use_svg_display()


def get_dataloader_workers():
    return 4

#加载数据集
def load_data_fashion_mnist(batch_size,resize=None):
    trans=[transforms.ToTensor()]
    if resize:
        trans.insert(0,transforms.Resize(resize))
    # 这个transforms.Compose()类的主要作用是串联多个图片变换的操作
    trans=transforms.Compose(trans)
    # 下载数据集
    mnist_train=torchvision.datasets.FashionMNIST(root="./data",train=True,transform=trans,download=False)
    mnist_test=torchvision.datasets.FashionMNIST(root="./data",train=False,transform=trans,download=False)
     # 返回构造的迭代器对象
    return (data.DataLoader(mnist_train,batch_size,shuffle=True,num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test,batch_size,shuffle=False,num_workers=get_dataloader_workers()))

batch_size=256
train_iter,test_iter=load_data_fashion_mnist(batch_size)


num_inputs=784#28*28空间拉长，softmax回归需要空间向量，这样子会损失一部分空间信息，交给后面的卷积
num_outputs=10#10个类别 
w=torch.normal(0,0.01,size=(num_inputs,num_outputs),requires_grad=True)
b=torch.zeros(num_outputs,requires_grad=True)
#运算
def softmax(x):
    x_exp=torch.exp(x)
    partition=x_exp.sum(1,keepdim=True)
    return x_exp/partition#广播机制

def net(x):
    return  softmax(torch.matmul(x.reshape((-1,w.shape[0])),w)+b)

def cross_entropy(y_hat,y):
    return -torch.log(y_hat[range(len(y_hat)),y])

def accuracy(y_hat,y):#找出预测正确的样本
    if(len(y_hat.shape)>1 and   y_hat.shape[1]>1):#输入是矩阵
        y_hat=y_hat.argmax(axis=1)#将预测结果概率值最大的值取出，# len(y_hat.shape)输出为y_hat的行向量的个数
    cmp=y_hat.type(y.dtype)==y#y_hat转化为y的类型 
    return float(cmp.type(y.dtype).sum())#求和

class Accumulator:#累加器
    def __init__(self,n):
        self.data=[0.0]*n
    def add(self,*args):
        self.data=[a+float(b) for a,b in zip(self.data,args)]
    def reset(self):
        self.data=[0.0]*len(self.data)
    def __getitem__(self,idx):
        return self.data[idx]
    
def evaluate_accuracy(net,data_iter):
    if isinstance(net,torch.nn.Module):
        net.eval()#将模型设置成评估模式
    metric=Accumulator(2)# 累加器，正确预测数metric[0]、预测总数metric[1]
    for x,y in data_iter:
        metric.add(accuracy(net(x),y),y.numel())
    return metric[0]/metric[1]  # 返回的是分类正确的样本数量/总样本数量


#单个epoch训练
def train_epoch_ch3(net,train_iter,loss,updater):
    # 如果是torch.nn.Module则开始训练
    if isinstance(net,torch.nn.Module):
        net.train()
    metric=Accumulator(3)#大小为3的累加器储存数据 
    # 接下来扫一遍数据
    for x,y in train_iter:
        y_hat=net(x)
        l=loss(y_hat,y)
        if isinstance(updater,torch.optim.Optimizer):#两种实现，
            #如果是pytorch的optimizer的话，先把梯度置为0
            updater.zero_grad()
            l.backward()
            updater.step()
            metric.add(float(l)*len(y),accuracy(y_hat,y),y.size().numel())#记录分类
        else:
            l.sum().backward()
            updater(x.shape[0])
            metric.add(float(l.sum()),accuracy(y_hat,y),y.numel())
    return metric[0]/metric[2],metric[1]/metric[2]#正确与错误的概率，返回的是  loss/样本数   所有正确的样本/样本数
 


class Animator:#不重要,实时显示用的
    def __init__(self,xlabel=None,ylabel=None,legend=None,xlim=None,ylim=None,xscale='linear',yscale='linear',
                fmts=('-','m--','g-.','r:'),nrows=1,ncols=1,figsize=(3.5,2.5)):
        if legend is  None:
            legend=[]
        d2l.use_svg_display()
        self.fig,self.axes=d2l.plt.subplots(nrows,ncols,figsize=figsize)
        if nrows*ncols==1:
            self.axes=[self.axes,]
        self.config_axes=lambda:d2l.set_axes(self.axes[0],xlabel,ylabel,xlim,ylim,xscale,yscale,legend)
        self.x,self.y,self.fmts=None,None,fmts
        
    def add(self,x,y):
        if not hasattr(y,"_len_"):
            y=[y]
        n=len(y)
        if not hasattr(x,"_len_"):
            x=[x]*n
        if not self.x:
            self.x=[[] for _ in range(n)]
        if not self.y:
            self.y=[[] for _ in range(n)]
        for i,(a,b) in enumerate(zip(x,y)):
            if a is not None and b is not None:
                self.x[i].append(a)
                self.y[i].append(b)
        self.axes[0].cla()
        for x,y,fmt in zip(self.x,self.y,self.fmts):
            self.axes[0].plot(x,y,fmt)
        self.config_axes()
        display.display(self.fig)
        # d2l.plt.draw()
        # d2l.plt.pause(0.001)
        display.clear_output(wait=True)

# 训练
def train_ch3(net,train_iter,test_iter,loss,num_epochs,updater):
    animator=Animator(xlabel='epoch',xlim=[1,num_epochs],ylim=[0.3,0.9],legend=['trans loss','trans acc','test acc'])
    for epoch in range(num_epochs):
        train_metrics=train_epoch_ch3(net,train_iter,loss,updater)
        test_acc=evaluate_accuracy(net,test_iter)
        animator.add(epoch+1,train_metrics+(test_acc,))
    train_loss,train_acc=train_metrics
    assert  train_loss<0.5,train_loss
    assert train_acc<=1 and train_acc>0.7, train_acc
    assert test_acc<=1 and test_acc>0.7,test_acc
    
lr=0.1
def updater(batch_size):
    return d2l.sgd([w,b],lr,batch_size)

num_epochs=10
train_ch3(net,train_iter,test_iter,cross_entropy,num_epochs,updater)
d2l.plt.show()

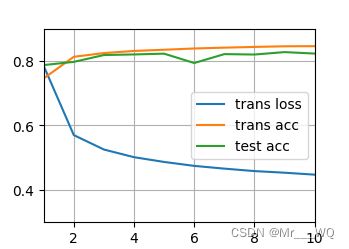
运行结果：

 

2.6 总结

        1.softmax回归是一个多分类模型；

        2.使用softmax操作子得到每一个类的预测置信度；

        3.使用交叉熵来衡量预测和标号的区别。