Educode--数据挖掘算法原理与实践：k-近邻
第1关：knn算法概述
任务描述
本关任务：使用python实现方法，找出目标样本最近的k个样本。
相关知识
为了完成本关任务，你需要掌握：1.knn算法思想，2.距离度量。
knn算法思想
k-近邻（k-nearest neighbor ,knn）是一种分类与回归的方法。我们这里只讨论用来分类的knn。所谓k最近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最近的k个邻居来代表。
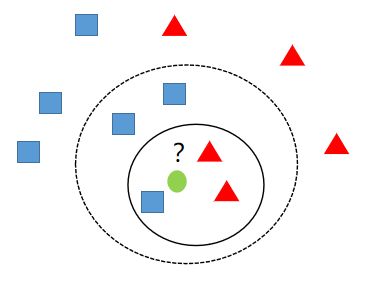
knn算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。knn方法在类别决策时，只与极少量的相邻样本有关。
如上图，当k=3时离绿色的圆最近的三个样本中，有两个红色的三角形，一个蓝色的正方形，则此时绿色的圆应该分为红色的三角形这一类。而当k=5时，离绿色的圆最近的五个样本中，有两个红色的三角形，三个蓝色的正方形，则此时绿色的圆应该分为蓝色的正方形这一类。
距离度量
我们已经知道，如何判别一个样本属于哪个类型，主要是看离它最近的几个样本中哪个类型的数量最多，则该样本属于数量最多的类型。这里，有一个问题：何为最近？
关于何为最近，大家应该自然而然就会想到可以用两个样本之间的距离大小来衡量，我们常用的有两种距离：
- 欧氏距离：欧氏距离是最容易直观理解的距离度量方法，我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。
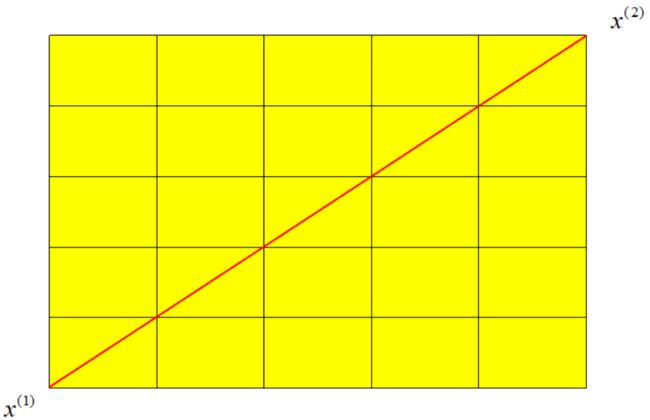
二维平面上欧式距离计算公式：
d12=(x1(1)−x1(2))2+(x2(1)−x2(2))2
n维平面上欧氏距离计算公式：
d12=i=1∑n(xi(1)−xi(2))2
- 曼哈顿距离：顾名思义，在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”。
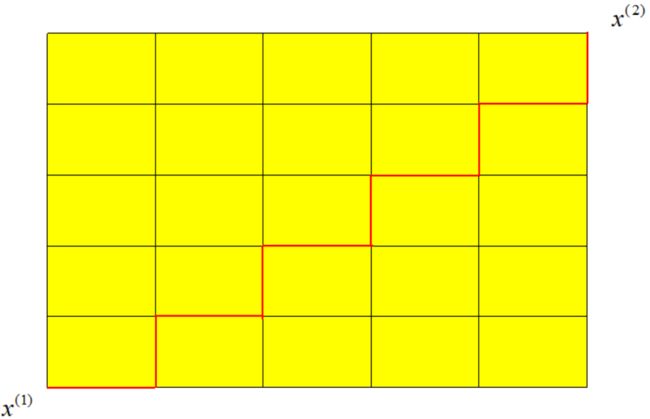
二维平面上曼哈顿距离计算公式：
d12=∣x1(1)−x1(2)∣+∣x2(1)−x2(2)∣
n维平面上曼哈顿计算公式：
d12=i=1∑n∣xi(1)−xi(2)∣
其中，上标圆括号内数字代表第几个样本，下标数字代表样本的第几个特征。
编程要求
根据提示，在右侧编辑器Begin-End处补充代码，实现topK方法。
测试说明
程序会调用你实现的方法，找出目标样本最近的k个样本的标签。如目标样本最近的5个样本为0，0，1，1，1则返回列表[0,0,1,1,1]。若返回结果与真实结果一致则视为通关。
开始你的任务吧，祝你成功！
实现代码：
#encoding=utf8
import numpy as np
def topK(i,k,x,y):
'''
input:
i(int):第i个样本
k(int):最近邻样本个数
x(ndarray):数据特征
y(ndarray):数据标签
output:
topK(list):样本i的最近k个样本标签
'''
#*********Begin*********#
#计算样本到所有样本的距离
distance = np.sqrt(np.power(np.tile(x[i],(x.shape[0],1))-x,2).sum(axis=1))
#除样本本身外的最近的k个样本的索引
nearest = np.argsort(distance)[1:k+1]
#除样本本身外的最近的k个样本的标签
topK = [y[j] for j in nearest]
#*********End*********#
return topK
代码截图：
第2关：动手实现knn算法
任务描述
本关任务：使用python实现knn算法，并对手写数字进行识别。
相关知识
为了完成本关任务，你需要掌握：1.加权投票，2.knn算法流程。
数据集介绍
手写数字数据集一共有1797个样本，每个样本有64个特征。每个特征的值为0-255之间的像素，我们的任务就是根据这64个特征值识别出该数字属于0-9十个类别中的哪一个。
我们可以使用sklearn直接对数据进行加载，代码如下：
from sklearn.datasets import load_digits#加载手写数字数据集digits = load_digits()#获取数据特征与标签x,y = digits .data,digits .target
当然，每一个样本就是一个数字，我们可以把它还原为8x8的大小进行查看：
import matplotlib.pyplot as pltimg = x[0].reshape(8,8)plt.imshow(img)
然后我们划分出训练集与测试集，训练集用来训练模型，测试集用来检测模型性能。代码如下：
from sklearn.model_selection import train_test_split#划分训练集测试集，其中测试集样本数为整个数据集的20%train_feature,test_feature,train_label,test_label = train_test_split(x,y,test_size=0.2,random_state=666)
加权投票
通过上一关，我们已经知道如何找出最近的k个样本，但是，现在还有一个问题要我们来解决：如果有两个类型的样本数一样且最多，那么最终该样本应该属于哪个类型？
其实，knn算法最后决定样本属于哪个类别，其实好比就是在投票，哪个类别票数多，则该样本属于哪个类别。而如果出现票数相同的情况，我们可以给每一票加上一个权重，用来表示每一票的重要性，这样就可以解决票数相同的问题了。很明显，距离越近的样本所投的一票应该越重要，此时我们可以将距离的倒数作为权重赋予每一票。
如上图，虽然蓝色正方形与红色三角形数量一样，但是根据加权投票的规则，绿色的圆应该属于蓝色正方形这个类别。
knn算法流程
knn算法不需要训练模型，只是根据离样本最近的几个样本类型来判别该样本类型，所以流程非常简单：
计算出新样本与每一个样本的距离找出距离最近的k个样本根据加权投票规则得到新样本的类别
编程要求
根据提示，在右侧编辑器Begin-End处补充代码，实现knn算法。
测试说明
程序会调用你的实现的方法对手写数字进行识别，正确率大于0.95则视为通关。
开始你的任务吧，祝你成功！
实现代码：
#encoding=utf8
import numpy as np
def knn_clf(k,train_feature,train_label,test_feature):
'''
input:
k(int):最近邻样本个数
train_feature(ndarray):训练样本特征
train_label(ndarray):训练样本标签
test_feature(ndarray):测试样本特征
output:
predict(ndarray):测试样本预测标签
'''
#*********Begin*********#
#初始化预测结果
predict = np.zeros(test_feature.shape[0],).astype('int')
#对测试集每一个样本进行遍历
for i in range(test_feature.shape[0]):
#测试集第i个样本到训练集每一个样本的距离
distance = np.sqrt(np.power(np.tile(test_feature[i],(train_feature.shape[0],1))-train_feature,2).sum(axis=1))
#最近的k个样本的距离
distance_k = np.sort(distance)[:k]
#最近的k个样本的索引
nearest = np.argsort(distance)[:k]
#最近的k个样本的标签
topK = [train_label[i] for i in nearest]
#初始化进行投票的字典，字典的键为标签，值为投票分数
votes = {}
#初始化最大票数
max_count = 0
#进行投票
for j,label in enumerate(topK):
#如果标签在字典的键中则投票计分
if label in votes.keys():
votes[label] += 1/(distance_k[j]+1e-10)#防止分母为0
#如果评分最高则将预测值更新为对应标签
if votes[label] > max_count:
max_count = votes[label]
predict[i] = label
#如果标签不在字典中则将标签加入字典的键，同时计入相应的分数
else:
votes[label] = 1/(distance_k[j]+1e-10)
if votes[label] > max_count:
max_count = votes[label]
predict[i] = label
#*********End*********#
return predict
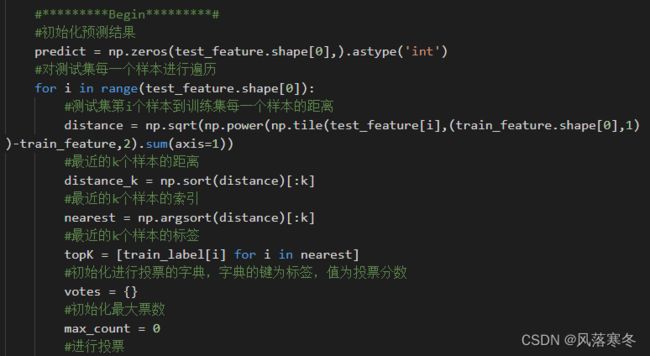
代码截图：
