【线性代数】矩阵的特征值分解(对角化、谱分解)
目录
- 1 前言
- 2 矩阵的特征值分解
-
- 2.1 从定义的角度理解
- 2.2 从变换的角度理解(来自参考文献[3])
- 3 对角矩阵(补充)
-
- 3.1 对角矩阵的定义
- 3.2 对角矩阵线性变换的几何意义
- 4 矩阵对角化
- 5 相似矩阵与特征值
- 6 参考文献
1 前言
矩阵的特征值分解又可以称作矩阵的对角化、谱分解。目的是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法(百度百科)。其在机器学习和图机器学习中有非常广泛的应用。本节主要介绍矩阵的特征分解的解法,意义,实际应用。除此之外,矩阵的特征值分解与矩阵的特征值和特征向量有关联,相关内容可以参考【线性代数】理解特征值和特征向量。
内容为自己的学习总结,其中多有借鉴他人的地方,最后一并给出链接。如果相关内容影响了相关作者,请私信联系,我将会加以修改。
2 矩阵的特征值分解
矩阵的特征值分解是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。
2.1 从定义的角度理解
从特征值分解的定义,可以了解到矩阵的特征值分解就是将矩阵的特征值和特征向量分开。从特征值和特征向量的定义: A x = λ x Ax=\lambda x Ax=λx,可以明确 A 、 λ 、 x A、\lambda 、x A、λ、x三者之间建立了一种关系。但是仅用单独的一个 λ 、 x \lambda、x λ、x是无法表示矩阵 A A A,因为这个式子不是完备的。对于一个秩为 m m m的矩阵 A A A ,应该存在 m m m个这样的式子,完备式子应该是:
A ( x 1 , x 2 , … , x m ) = ( λ 1 x 1 , λ 2 x 2 , … , λ m x m ) = ( x 1 , x 2 , … , x m ) [ λ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ λ m ] 上面的式子可以写作 A X = X Λ A\left(x_{1}, x_{2}, \ldots, x_{m}\right)=\left(\lambda_{1} x_{1}, \lambda_{2} x_{2}, \ldots, \lambda_{m} x_{m}\right)\\[8mm] =\left(x_{1}, x_{2}, \ldots, x_{m}\right)\left[\begin{array}{ccc} \lambda_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_{m} \end{array}\right] \\[10mm] 上面的式子可以写作~~~~~~A X=X \Lambda\\ A(x1,x2,…,xm)=(λ1x1,λ2x2,…,λmxm)=(x1,x2,…,xm)⎣ ⎡λ1⋮0⋯⋱⋯0⋮λm⎦ ⎤上面的式子可以写作 AX=XΛ
进一步的做变换 A = X Λ X − 1 进一步的做变换~~~A=X \Lambda X^{-1} 进一步的做变换 A=XΛX−1
这种形式就可以看成矩阵 A A A被分解了。
2.2 从变换的角度理解(来自参考文献[3])
从运动变换的角度理解,矩阵乘以向量可以分三步:
- 首先将这个向量使用特征向量组成的正交基向量进行分解
- 然后目标向量在每个特征向量方向上的分量分别进行拉伸操作
- 对所有特征向量方向上的拉伸结果进行合并
举个例子:
如果使用这个矩阵对向量进行变换操作,我们会发现
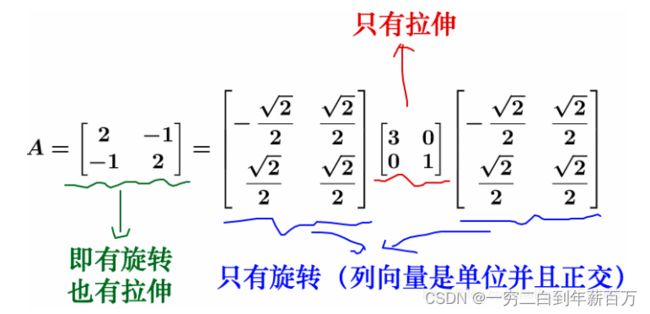
特征值分解其实就是将矩阵的变换操作分解了,将旋转与拉伸分离开来,最后达到上述意义的效果。
为什么说方阵才能进行特征值分解:
这是因为只有方阵或者说实对称方阵才能够在矩阵空间提取出符合完全正交基的特征向量,这样对于任何一个目标向量进行变换时,才能使用特征向量对目标向量进行完全表示。如果不能提取出满足条件的特征向量,则特征值分解的公式是不成立的!
对于不能进行特征值分解的时,可以采用奇异值分解。
特征值和特征向量是为了研究向量在经过线性变换后的方向不变性而提出的
- 一个矩阵和该矩阵的非特征向量相乘是对该向量的旋转变换
- 一个矩阵和该矩阵的特征向量相乘是对该向量的伸缩变换,其中伸缩程度取决于特征值大小
3 对角矩阵(补充)
3.1 对角矩阵的定义
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为 0 0 0的矩阵,写作 d i a g ( a 1 , a 2 , . . . , a n ) diag(a_1, ~a_2,...,~a_n) diag(a1, a2,..., an)。对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。
3.2 对角矩阵线性变换的几何意义
对角矩阵是对基向量进行拉伸,也就是我们常说的坐标轴单位向量进行拉伸(收缩),从几何直观上来讲,只有坐标轴上的向量还在原来的方向上。(可以参考【线性代数】理解特征值和特征向量中给出的例子)。
4 矩阵对角化
5 相似矩阵与特征值
相似矩阵定义:设 A A A, B B B都是 n n n阶矩阵,若有可逆矩阵 P P P, 使 P − 1 A P = B P^{-1}AP=B P−1AP=B ,则称 B B B是 A A A的相似矩阵。
物理意义 :相似矩阵的几何意义是同一个线性变换在不同的基下的表达形式。
相似矩阵的性质:
- 相似矩阵有相同的行列式
- 有相同的秩、相同的迹、相同的特征方程、特征值、相同的Jondan标准型、相同的特征多项式、相同的最小多项式
这些统称为相似不变量,“相似矩阵有若干相似不变量”,特征值是最重要的相似不变量,利用这个相似不变量可以方便的得出上面所有的不变量。
不变量的几何意义:
- 相同行列式:相似矩阵的线性映射,膨胀系数不变
- 相同的秩:相似矩阵的线性映射,对空间的维数的影响一致
- 相同的特征方程:相似矩阵的线性映射,对向量的主变化方向和变化速度影响一致
6 参考文献
[1]特征值(eigenvalue)特征向量(eigenvector)特征值分解(eigenvalue decomposition)
[2]一文解释 矩阵特征分解
[3]矩阵的特征值分解
[4]Diagonalization 矩阵对角化
[5]实对称矩阵相同特征值对应的特征向量正交吗?