机器学习----熵,信息增益与决策树(Decision Tree)
文章目录
- 1. 简介
- 2. 熵
- 3. 信息增益
- 4. 决策树算法
- 5. 决策树剪枝策略
-
- (1)目的
- (2)方法
- 6. 代码实现
1. 简介
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
2. 熵
表示随机变量不确定性的度量,熵越大越不稳定。
公式:H(x)=-∑pi*logpi(i=1,2,…,n),log经常取以2位底
pi为随机变量X在样本空间的分布,即第i个类型出现的概率。
H(x)越大,说明熵值越大,越混乱。
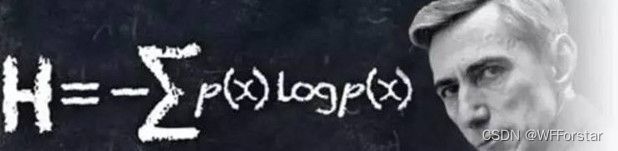
对二分类问题来说:
当pi=0或pi=1时,熵值最小为0;
当pi0.5时,熵值最大为1;
3. 信息增益
信息增益是一个统计量,用来描述一个属性区分数据样本的能力。信息增益越大,那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量。
用人话来说,就是用分离完特征数据后的熵值减分离前的熵值,来比较熵的减少程度。
4. 决策树算法
ID3:信息增益 (容易过拟合)
C4.5:信息增益率 一定程度上解决了信息带来的问题
CART:GINI系数
GINI系数公式:

Gini系数与熵的含义类似,越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯,只是计算方法不同。
5. 决策树剪枝策略
(1)目的
为了解决过拟合问题,理论上决策树可以完全分开数据。
(2)方法
预剪枝:边建立决策树边进行剪枝操作(推荐使用)
具体:限制深度,限制叶子节点个数,限制叶子节点样本数,信息增量等
后剪枝:建立完决策后进行剪枝操作
具体:通过一定的标准
6. 代码实现
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz
# data
def create_data():
iris = load_iris() # 导入鸢尾花数据集
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]]) # 选择100行数据,第一列,第二列与最后一列label作为数据集
# print(data)
return data[:,:2], data[:,-1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
clf = DecisionTreeClassifier()
clf.fit(X_train, y_train)
clf.score(X_test, y_test) # 1代表最高分
tree_pic = export_graphviz(clf, out_file='mytree.pdf',filled=True)
with open('mytree.pdf') as f:
dot_graph = f.read()
graphviz.Source(dot_graph)