f-loam代码分析
两年前,南洋理工的王晗等人在loam的基础上,为减少计算量,提出了一个也是纯激光SLAM的工程,也在IROS上发表一篇文章《F-LOAM : Fast LiDAR Odometry and Mapping》。整体来看和loam的算法没有太大差异,只是工程上进行缩减,在我自己的数据包上实际测试效果也还不错吧。
A 传感器模型与特征提取
机械式三维激光雷达通过旋转一个尺寸为M的垂直排列的激光束阵列来感知周围的环境。它用M个平行读数扫描垂直面。在每个扫描间隔期间,激光阵列在水平面上以恒定速度旋转,同时激光测量按顺时针或逆时针顺序进行。
如上所述,三维机械激光雷达返回的点云在垂直方向上是稀疏的,在水平方向上是稠密的。因此,水平方向的特征更加明显,在水平方向上进行错误特征检测的可能性较小。对于每一个点云,我们聚焦在水平面上,并通过计算局部曲面的平滑度。
C 姿态估计
通过从边缘和平面特征图中收集附近的点来估计全局线和平面。对于每个边缘特征点, 从全局边缘特征图中计算其附近点的协方差矩阵。当点分布在一条直线上时,协方差矩阵包含一个更大的特征值。将与最大特征值相关的特征向量视为直线方向,直线的位置视为附近点的几何中心。类似地,对于每个平面特征点,这里可以得到一个具有位置和曲面范数的全局平面。注意,与全局边不同,全局平面的范数作为与最小特征值相关的特征向量。
f-loam是基于LOAM和ALOAM改进而来,计算时间缩小3倍,精度也有一定提高。本系统只是小提升。 其主要的原理和流程没有变化。首先是点云预处理、然后提取边缘和平面特征,分别进行匹配估计位姿,最后位姿融合。当然这里还提供了mapping和localization的模块,但mapping部分只是将估计的位姿,拼接点云,并没有后端优化等模块。
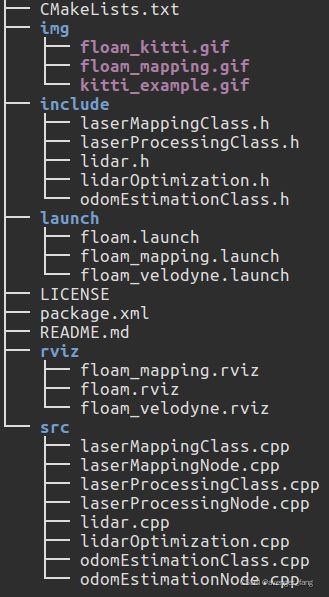
从以上的代码结构来看,主要有以下功能文件
- lidar.cpp: 系统的参数配置,比如雷达线束数量、扫描周期等
- laserProcessingClass.cpp、laserProcessingNode.cpp:输入原始的多线点云,进行点云预处理节点,与loam一致,包括边缘、平面特征提取
- odomEstimationNode.cpp、odomEstimationClass.cpp:里程计位姿估计节点,根据边缘点、平面点特征,构建点线、点面残差,利用ceres联合滑窗优化,估计位姿。得到机器人在里程计坐标系下的位姿,这里的里程计坐标系就是通常SLAM的map坐标系,它们是重合的。
- laserMappingNode.cpp、laserMappingClass.cpp:点云地图构建节点,根据odom信息拼接经过特征提取的点云,略微不一样的地方在使用栅格点云来表示地图。
- lidarOptimization.cpp:odom评价
由此可以看到,此工程没有后端优化的过程,经过前端匹配scan to local map得到残差进行优化直接得到了位姿估计。
综合以下解析整理。开源SLAM系统:FLOAM源码解析 | 攻城狮の家最近在github上看到了此套系统,看简介说是基于LOAM和ALOAM改进而来,计算时间缩小3倍,精度也有一定提高。本系统只是小提升,并没有相关论文发表。作者加入了一些场景识别的改进,发表在2020年ICRA上,叫ISCLOAM,代码也开源到github,后续单独写一篇进行记录。 我在kitti上跑了一下: 红色的表示ground_truth,绿色的是odom轨迹。 项目地址如下:https:http://xchu.net/2020/08/17/49floam/
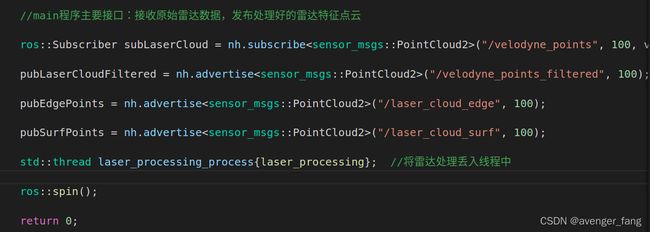
(1)laserProcessingNode.cpp
laser_processing_process线程中循环执行,取点云数据->提取边缘和平面特征->发布相关点云。首先是取点云数据。
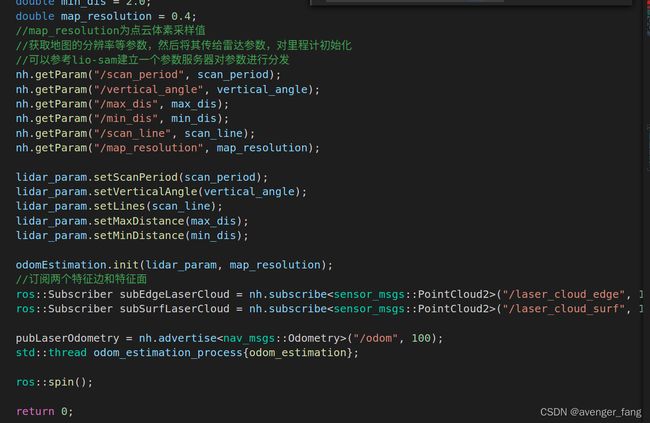
(2)odomEstimationNode.cpp
位姿估计节点主要接收边缘和平面特征,分别构建点到直线,点到平面的残差项,并通过ceres求解旋转四元数q和位移t,最后发出经过优化求解的里程计位姿。
用一个滑窗来维护corner和surface特征的local map,第一帧点云直接加入local map进行初始化。后续点云帧进来就构建约束。
构建点到直线的约束。寻找最近的5个点,对点云协方差矩阵进行主成份分析: 若这5个点分布在直线上,协方差矩阵的特征值包含一个元素显著大于其余两个,与该特征值相关的特征向量表示所处直线的方向; 若这5个点分布在平面上,协方差矩阵的特征值存在一个显著小的元素,与该特征值相关的特征向量表示所处平面的法线方向。参考2016,IROS,fast and robust 3d feature extraction from sparse point clouds.
//添加因子,将当前帧转到里程计坐标系下之后与local map构建残差
void OdomEstimationClass::addEdgeCostFactor(const pcl::PointCloud::Ptr& pc_in, const pcl::PointCloud::Ptr& map_in, ceres::Problem& problem, ceres::LossFunction *loss_function){
int corner_num=0;
for (int i = 0; i < (int)pc_in->points.size(); i++)
{
pcl::PointXYZI point_temp;//输入的坐标为基于雷达的坐标系
//很容易理解,就是将当前点配准转到local map坐标系
pointAssociateToMap(&(pc_in->points[i]), &point_temp);
std::vector pointSearchInd;
std::vector pointSearchSqDis;
//与当前点最近邻搜索5个附近点
kdtreeEdgeMap->nearestKSearch(point_temp, 5, pointSearchInd, pointSearchSqDis);
if (pointSearchSqDis[4] < 1.0) //若最远的点都是小于1m的,则认为它是邻近点
{
std::vector nearCorners;
Eigen::Vector3d center(0, 0, 0);//初始化中心点为0
for (int j = 0; j < 5; j++)
{
Eigen::Vector3d tmp(map_in->points[pointSearchInd[j]].x,
map_in->points[pointSearchInd[j]].y,
map_in->points[pointSearchInd[j]].z); //返回这五个点的具体坐标
center = center + tmp; //一步步累加为了后面求均值
nearCorners.push_back(tmp);//将附近的点放到邻近角点向量中
}
center = center / 5.0; //累加后取均值作为最终的一个邻近点,与当前点的邻近点
Eigen::Matrix3d covMat = Eigen::Matrix3d::Zero(); //给定协方差,初值2为0
for (int j = 0; j < 5; j++)
{
Eigen::Matrix tmpZeroMean = nearCorners[j] - center;//各方向给的距离中心的偏差值的平方向量作为方差
covMat = covMat + tmpZeroMean * tmpZeroMean.transpose(); //协方差矩阵相加
}//添加五个点的协方差
Eigen::SelfAdjointEigenSolver saes(covMat);//矩阵特征值分解和特征向量获取
Eigen::Vector3d unit_direction = saes.eigenvectors().col(2); //得到特征向量Z方向的特征值
Eigen::Vector3d curr_point(pc_in->points[i].x, pc_in->points[i].y, pc_in->points[i].z);
//主成分分析,若有一个特征值明显大于另外一个特征值,说明是一条直线
if (saes.eigenvalues()[2] > 3 * saes.eigenvalues()[1])//通过特征值做对比判断
{
Eigen::Vector3d point_on_line = center; //将当前帧的邻近点作为直线上的一点,那么
Eigen::Vector3d point_a, point_b; //拟合的直线上 有上下两个点A、B
point_a = 0.1 * unit_direction + point_on_line; //OA = OC + 0.1 * AB
point_b = -0.1 * unit_direction + point_on_line;
//构建损失函数进行残差添加
//理想情况下当前点和AB点应该是共线的,因此curr_point 与 AB 线段距离应该为0,通过curr_point 与 AB 线段距离的残差
//注意这三个点都是在上一帧的map坐标系下,即,残差 = 点O到直线AB的距离
ceres::CostFunction *cost_function = new EdgeAnalyticCostFunction(curr_point, point_a, point_b);
problem.AddResidualBlock(cost_function, loss_function, parameters);
corner_num++;
}
}
}
if(corner_num<20){
printf("not enough correct points");
}
} 点到平面的约束,通过kdtree获取Local map上最近的5个点,通过QR分解求解最小二乘问题获得平面参数,最后构建点到平面的残差。
然后进行残差计算优化
bool EdgeAnalyticCostFunction::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{
Eigen::Map q_last_curr(parameters[0]);
Eigen::Map t_last_curr(parameters[0] + 4);
Eigen::Vector3d lp;
lp = q_last_curr * curr_point + t_last_curr;
Eigen::Vector3d nu = (lp - last_point_a).cross(lp - last_point_b);
Eigen::Vector3d de = last_point_a - last_point_b;
double de_norm = de.norm();
residuals[0] = nu.norm()/de_norm;
if(jacobians != NULL)
{
if(jacobians[0] != NULL)
{
Eigen::Matrix3d skew_lp = skew(lp);
Eigen::Matrix dp_by_se3;
dp_by_se3.block<3,3>(0,0) = -skew_lp;
(dp_by_se3.block<3,3>(0, 3)).setIdentity();
Eigen::Map > J_se3(jacobians[0]);
J_se3.setZero();
Eigen::Matrix3d skew_de = skew(de);
J_se3.block<1,6>(0,0) = - nu.transpose() / nu.norm() * skew_de * dp_by_se3/de_norm;
}
}
return true;
} (3)laserMappingClass.cpp
在存储点云地图时,将地图按照点云栅格进行存储
void LaserMappingClass::init(double map_resolution){
//init map
//init can have real object, but future added block does not need
for(int i=0;i::Ptr>> map_height_temp;
for(int j=0;j::Ptr> map_depth_temp;//深度地图 高度方向 5个
for(int k=0;k::Ptr point_cloud_temp(new pcl::PointCloud);
map_depth_temp.push_back(point_cloud_temp);
}
map_height_temp.push_back(map_depth_temp);
}
map.push_back(map_height_temp);//map为三维的栅格点云,每个栅格存储的是点云
}
origin_in_map_x = LASER_CELL_RANGE_HORIZONTAL; //2
origin_in_map_y = LASER_CELL_RANGE_HORIZONTAL; //2
origin_in_map_z = LASER_CELL_RANGE_VERTICAL; //2
map_width = LASER_CELL_RANGE_HORIZONTAL*2+1;
map_height = LASER_CELL_RANGE_HORIZONTAL*2+1;
map_depth = LASER_CELL_RANGE_HORIZONTAL*2+1; //5
//downsampling size
downSizeFilter.setLeafSize(map_resolution, map_resolution, map_resolution);
} 将点云按照一个个大栅格划分,一个小栅格的尺寸是50mX50mX50m的立方体栅格,最大为5个栅格,存储5×50=250m范围内的点云地图。存储时只是简单的拼接。
//update points to map
void LaserMappingClass::updateCurrentPointsToMap(const pcl::PointCloud::Ptr& pc_in, const Eigen::Isometry3d& pose_current){
//当前位置,根据雷达LASER_CELL_WIDTH的宽度50得到当前位置的索引,就是在50m范围内划分格子,一个格子50m
int currentPosIdX = int(std::floor(pose_current.translation().x() / LASER_CELL_WIDTH + 0.5)) + origin_in_map_x;
int currentPosIdY = int(std::floor(pose_current.translation().y() / LASER_CELL_HEIGHT + 0.5)) + origin_in_map_y;
int currentPosIdZ = int(std::floor(pose_current.translation().z() / LASER_CELL_DEPTH + 0.5)) + origin_in_map_z;
//check is submap is null
checkPoints(currentPosIdX,currentPosIdY,currentPosIdZ);
pcl::PointCloud::Ptr transformed_pc(new pcl::PointCloud());
pcl::transformPointCloud(*pc_in, *transformed_pc, pose_current.cast());
//save points
for (int i = 0; i < (int)transformed_pc->points.size(); i++)
{
pcl::PointXYZI point_temp = transformed_pc->points[i];
//for visualization only
point_temp.intensity = std::min(1.0 , std::max(pc_in->points[i].z+2.0, 0.0) / 5);
int currentPointIdX = int(std::floor(point_temp.x / LASER_CELL_WIDTH + 0.5)) + origin_in_map_x;
int currentPointIdY = int(std::floor(point_temp.y / LASER_CELL_HEIGHT + 0.5)) + origin_in_map_y;
int currentPointIdZ = int(std::floor(point_temp.z / LASER_CELL_DEPTH + 0.5)) + origin_in_map_z;
map[currentPointIdX][currentPointIdY][currentPointIdZ]->push_back(point_temp);
}
//filtering points
for(int i=currentPosIdX-LASER_CELL_RANGE_HORIZONTAL;i 其他的部分就不赘述了,有机会再继续探讨。