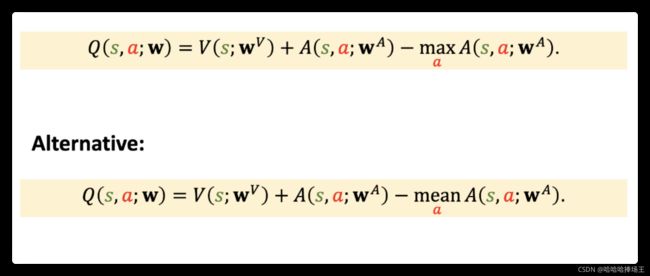DQN高级技巧

DQN高级技巧

DQN和TD Learning回顾

DQN

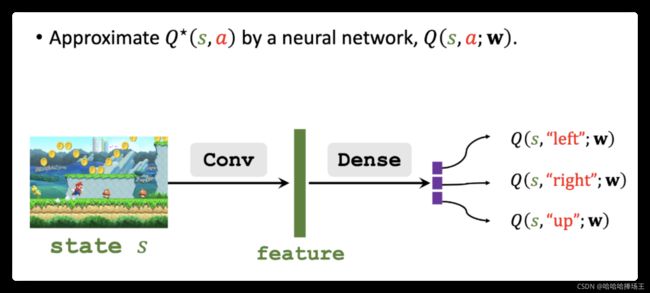
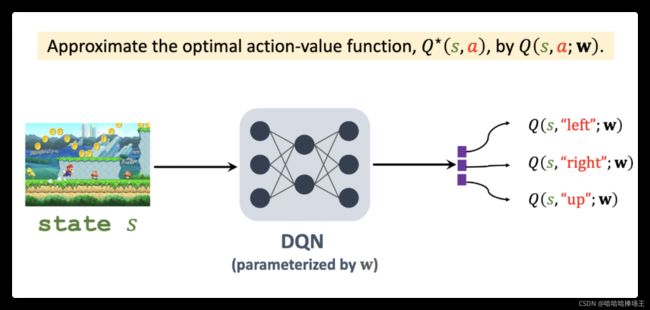
• 之前我们学过$Q^{\ast }(s,a)$函数，它叫做动作价值函数，它依赖于当前的状态s和动作a，它基于当前状态s给所有的动作a打分，分数反映了动作a的好坏，Agent应该执行分数最高的动作，DQN的意思是使用神经网络来近似$Q^{\ast }$函数，神经网络的参数记作：w。DQN的意思是用神经网络来近似$Q^{\ast }$函数，训练好DQN之后，使用DQN来控制Agent。DQN的输入是状态s，将s输入DQN。如下图将超级玛丽画面放入DQN中，DQN中有卷积层和全连接层，DQN的输出是所有动作的分数，如果有三种可能的动作，DQN的输出就是三维向量。
  

TD算法

• 通常使用TD算法来训练DQN，下面我们来回顾一下TD算法：
  • Agent观测到当前的状态$s_t$，并且执行动作$a_t$
  • 环境给出新的状态$s_{t+1}$和奖励$r_t$
  • 将TD target记作$y_t=r_t+\gamma \cdot \underset{a}{\max }Q(s+t+1,a;w)$. $y_t$部分基于真实的奖励$r_t$，部分基于DQN在t+1时刻做出的预测
  • 把DQN在t时刻做出的预测记作：$q_t=Q(s_t,a_t;w)$，则$q_t-y_t$称为TD error，叫做${\delta }_t$，DQN的$q_t$完全是凭空猜测的，没有实际观测，而TD target $y_t$，部分基于自己的观测，部分基于预测，所以我们认为$y_t$比$q_t$更靠谱。我们希望$q_t$能接近$y_t$也就是TD error尽量小。

• TD算法的目标就是让我们在上面得到的${\delta }_t$尽量小，所以要最小化${\delta }_t^2$，将所有${\delta }_t^2$记为L(w)，w是DQN的参数，它影响$q_t$从而影响${\delta }_t$. 我们想要找到w使得L(w)尽量小。前面我们使用在线梯度下降来更新w
  • 在时刻t，观测到$(s_t,a_t,r_t,s_{t+1})$这个4元组，用它们计算出TD error，
  • 将${\delta }^2/2$关于w求梯度，得到$g_t=\frac{\partial {\delta }_t^2/2}{\partial w}={\delta }_t\cdot \frac{\partial Q(s_t,a_t;w)}{\partial w}$，$g_t$表示梯度
  • 然后使用梯度下降来更新梯度，$w\leftarrow w-\alpha \cdot g_t$
  • 上面我们得到的四元组相当于一条数据，上面我们使用它更新了w之后，将四元组给丢掉。

经验回放(Experience Replay)

Shortcoming 1：Waste of Experience

• 上面介绍的TD算法的一个缺点就是：浪费经验
• 我们将上面使用的4元组称为一个transition，经验指的是从开始到结束所有的transitions，刚刚的TD算法在使用完一个transition之后就丢弃了，这就会造成浪费，然而事实上经验是可以被重复利用的。这就是做经验回放的主要原因。

Shortcoming 2: Correlated Updates

• 刚刚的原始的TD算法还有一个缺点，就是transition之间的相关性，之前我们按照顺序来使用每一条transition来更新w，第t条transition包括$(s_t,a_t,r_t,s_{t+1})$，前后两条transition之间有很强的相关性，实验证明这种相关性是有害的。

Experience Replay

• 使用经验回放可以有效的克服刚刚提到的两个缺点，既可以重复利用经验避免浪费，也可以将transition打散，避免相关性。
• 上面我们提到一个transition包括：$(s_t,a_t,r_t,s_{t+1})$，也是一条训练数据
• 将最新的transitions存到一个队列里，这个队列称为Replay Buffer，容量是n

• 如果Replay Buffer存满了，放入一个新的transition就删除一个条老的transition，容量n是一个超参数，有很多实验表明：n的大小对实验有影响。通常设置在10万-100万之间，取决于具体应用。

• 使用TD算法训练DQN的时候，应该这样做经验回放：

  • 上面我们得到了目标函数L(w)，我们希望最小化它
  • 我们可以使用SGD来最小化L(w)
    • 每次从Replay Buffer中随机抽取一个transition，记为：$(s_i,a_i,r_i,s_{i+1})$
    • 然后用这个transition来计算TD error，记为：${\delta }_i$
    • 求导得到随机梯度。记为：$g_i$
    • 最后做随机梯度下降，使用$g_i$来更新w，这里只用了一个transtion来更新，实际使用中通常使用多个transitions算出多个随机梯度，拿梯度的平均来更新w。

• 做Experience Replay有两个好处
  • 打破了transition序列的相关性
  • 能重复利用过去的经验

Prioritized Experience Replay(经验回放的一种改进)

• 它与传统的经验回放的区别在于，使用非均匀抽样代替均匀抽样。

• Basic Idea

  • Buffer中有许多的transitions，但是它们的重要性各不相同，比如下面超级玛丽里面，左边的transition非常的常见有很多，但是右边打boss的transition很少，这样的话训练出的DQN不知道怎么去打boss。在这个例子中右边的经验很少，所以更重要，要充分利用它，不然很容易被卡在boss关。
  • 实际训练中算法怎么知道哪个transition更加重要呢？可以使用TD error来判断，TD error的值越大就越重要，应该给较高的优先级。这是应为训练出的DQN不熟悉右边的场景，所以会偏离TD target所以训练出来的TD error就比较大。所以要给右边更高的权重，使它更好的应对右边的场景。
    

• 优先经验回放的基本想法就是使用非均匀抽样代替均匀抽样，下面介绍两种不同的抽样方法：

  • 法1: 让抽样概率$p_t$正比于TD error的绝对值再加上$ϵ$，这里$ϵ$是一个很小的数，它的作用是避免概率$p_t$为0
  • 法2: 对TD error的绝对值做一个排序，大的靠前，小的靠后，rank(t)是${\delta }_t$的序号，让$p_t$反比于rank(t)，${\delta }_t$的绝对值越大，它的序号就越小，抽样概率$p_t$的值就越大
  • 总而言之，两种方法的思想是一样的，${\delta }_t$的值越大，被抽到的概率就越大。

• 抽样的时候是非均匀的，不同的transition有不同的抽样概率，这样会导致DQN的预测有偏差。应该相应调整学习率，抵消掉不同抽样概率造成的偏差。
  • TD算法使用SGD来更新参数w，我们将学习率记为：$\alpha$，如果做均匀抽样所有的transition都应该有相同的学习率，如果做非均匀抽样，应该根据抽样概率来调整学习率。如果一个transition有较大的抽样概率，应该把它的学习率调的比较小。计算$(n{p}_t{)}^{-\beta }$，将它乘到学习率上，这里的$\beta \in (0,1)$，均匀抽样是一个种特殊情况，抽样概率都为$\frac{1}{n}$，这样$n{p}_t=1$，不会影响学习率。如果是非均匀抽样，学习率会有所不同，对于较大的$p_t$算出的值越小，会让学习率变小。这里的$\beta$是一个超参数。论文中建议将$\beta$从小到大。

• 为了做优先经验回放，要将每一条transition都计算TD error，如果一个transition还刚被收集到，还没有得到它的TD error，我们直接将它的权重设置为最大值，也就是它有最高的优先级。训练DQN的时候要对TD error做更新，每次我们使用一条transition的时候，我们需要重新计算它的TD error，这条transition就有了新的权重。

Summary

DQN的高估问题

• Target Network & Double DQN

Bootstapping

• 字面意思是：拔自己的鞋带，把自己举起来。也就是自举。听起来很荒谬。在统计和机器学习中非常的常用。在RL中bootstapping的意思是：用一个估算去估计同类的估算。也就是自己把自己给举起来。上面我们提高了使用一个transition来更新DQN的参数w。首先计算TD target记为：$y_t$，它部分基于观测到的奖励$r_t$，部分基于DQN在t+1时刻的估计，我们希望DQN在t时刻的估计接近$y_t$，两者的差就是TD error，希望TD error尽量小，所以采用SGD来更新参数w。在计算TD target的时候，我们既用到了真实值，也用到了DQN在t+1时刻的估计值，我们使用SGD去更新DQN的参数的时候用到了$y_t$，这说明为了更新DQN在t时刻的估计，我们使用DQN在t+1时刻的估计，这就是用一个估计值去更新另一个估计值，相当于Bootstapping。

Problen of Oversestimation

• 使用TD算法更新DQN，会使DQN高估动作的价值。前面提到的Target Network和Double DQN就是为了解决这个问题。
• 高估的原因：
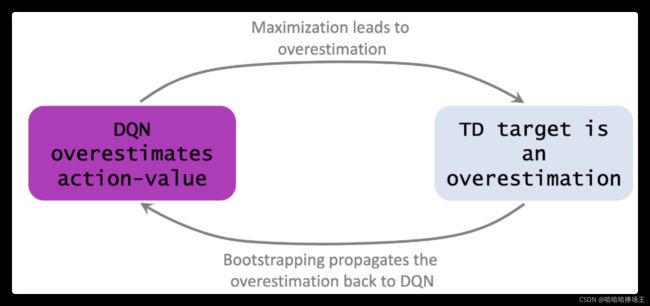
  • 原因1：之前计算TD target使用了最大化，这会导致高估。这个最大化会导致值大于真实的动作价值
  • 原因2：Bootstrapping。用自己的估计去更新自己，如果当前DQN已经高估，下一步的DQN将更加高估，一步一步使得高估更加严重。

• 最大化造成高估的原因

  • 设$x_1,x_2,x_3,\cdots ,x_n$是观测到的实数
  • 往$x_1,x_2,x_3,\cdots ,x_n$中添加均值为0的随机噪声，将获得的结果记为：$Q_1,Q_2,...,Q_n$
  • 由于噪声的均值为0，这样噪声就不会影响Q的均值，对Q的均值求期望结果就是x的均值
  • 但是噪声会让最大值增长，对Q的最大值求期望结果一定大于x的最大值
  • 同样，随机噪声会让最小值变得更小，这样对Q的最小值求期望结果一定小于x的最小值

• 回到DQN的高估问题上来，设$x(a_t),...,x(a_n)$是真实的动作价值。$a_1,...,a_n$是动作空间中的所有的动作，我们不知道真实的动作价值，所以我们会使用DQN来估算这些价值，将DQN的估计值记为：$Q(s,a_1;w),...,Q(s,a_n;w)$，估计肯定有误差。我们不妨假设DQN对真实值的误差的估计是无偏的，这样误差就相当于均值为0的噪声。计算TD target的时候，要对DQN的结果求最大化，把结果记为$q_t$，之前我们知道往结果里面加上噪声，会使得期望高于真实值的期望。所以q是对x(a)的高估。

• 

• 我们将DQN在t+1时刻的估计记为：$q_{t+1}$，我们刚刚得出结论，$q_{t+1}$是对真实值的高估。TD target部分依赖于$q_{t+1}$，所以TD target也是高估。TD算法鼓励DQN接近于TD target，既然TD target是高估，那么更新之后的DQN也是高估。

• 

• Bootstrapping

  • TD target用到了DQN在t+1时刻的估计值$q_{t+1}$，我们拿TD target来更新DQN在t时刻的估计，这就是用DQN来更新DQN自己。这就是Bootstrapping，这会使高估变得更严重。假设DQN已经高估了动作价值，计算TD target的时候用到了DQN自己，注意这个DQN的输出已经大于真实价值了，然后最大化，上面我们也提到了最大化会高估动作价值，这里进一步高估动作价值，然后用$q_{t+1}$来更新DQN，这样高估又被传播会DQN，使得高估变得更加严重。

Why does overestimation happen？

Why is overestimation a shortcoming?

• DQN的输入是当前的状态$s_t$，输出是执行所有动作的概率，最后会选择概率最高的动作执行。所以高估本身并不是问题，只要所有价值都被同等的高估。麻烦的事非均匀的高估，
  
• 实际上，DQN的高估是非均匀的，有的被高估很多，有的被高估一点。原因：TD算法每次从Replay Buffer中取出一个transition去更新DQN参数w，前面我们知道，TD target是对真实的动作价值的高估，TD算法鼓励DQN的预测接近TD target，就会将DQN的估计值推高。状态s和动作a的二元组，每被用来更新DQN，就会让DQN高估s和a的价值，s和a在Replay Buffer中的频率是不均匀的，s和a在replay buffer中越频繁出现，就会让DQN对s和a的高估越严重。结论就是s和a在DQN中的高估是非均匀的，所以我们希望能避免高估。

Solution

• 解决方案一：避免Bootstapping，不要使用DQN自己来计算TD target，使用另一个神经网络来计算TD targert，另一个神经网络也被称为target network
• 解决方案二：Double DQN，用来缓解最大化造成的高估。它也使用target network，但是具体用法有一些区别，这个区别可以大幅度改善效果

Target Network

• DQN是使用一个神经网络来近似动作价值函数，现在我们使用两个神经网络。第二个神经网络我们称为：Target Network. 两个神经网络的结构相同但是参数不同。将DQN的参数记作：w，将target network的参数记作：$w^{-}$，两个神经网络的用途不同，DQN用来控制Agent和收集经验（很多条transitions）。Target Network唯一的用途就是计算TD target。以前是自举，现在使用Target Network在一定程度上缓解了自举的问题。
  

TD Learning with Target Network

• 我们每次用一个transition来更新DQN的参数w，使用Target Network来计算TD target，这样可以避免Bootstapping，然后计算TD error，它是DQN的预测与TD target两者之差。最后使用SGD来更新DQN的参数w。注意这里SGD只更新DQN的参数，不更新Target network
  
• Target Network的参数是$w^{-}$，要隔一段时间更新一次
  • 方式一：直接将DQN的w结果给$w^{-}$
  • 方式二：将DQN的参数w和$w^{-}$做一个加权的平均，然后赋值给$w^{-}$

• 使用target network与原来的DQN唯一的区别就是计算TD target。原始的方法使用DQN自己去计算TD target现在使用Target Network去计算TD target
  

Double DQN

• Double DQN可以更好的缓解高估的问题。
• 原始的DQN计算TD target，可以分为两步：第一步是找出能最大化Q函数的动作。第二步是使用上一步选出的动作带入DQN去，这两步都使用DQN这样表现很差，会严重高估动作的价值。
  
• 上面我们介绍的使用TD NetWork来计算TD target。和原始的一样，第一步是选出最大化Q函数的动作，这里使用的是target network。第二步是将上一步得到的动作带入，这里用的还是Target Network。上面原始方法两步都是用的DQN，这里两步都是用的Target Network，使用Target Network会让表现变得更好，但是高估还是很严重。

• 下面我们介绍一种计算TD target的方式Double DQN。首先做选择，选出最大化Q函数的动作，这一步使用的是DQN。第二步是计算TD target要把上一步找到的动作带入Q函数，这里用的是Target Network。

• Why does double DQN work better?
  • Double DQN将计算TD target分解为两步
    • 第一步：选择动作$a^{\ast }$，用的是DQN本身
    • 第二步：计算TD target，用的是Target Network
    • 很容易证明下面的公式。

Summary

Dueling Network

Advantage Function

回顾

• 前面我们定义了折扣回报，它是从t时刻开始左右奖励的加权和，它依赖与未来的所有动作以及状态。我们还定义了动作价值函数为折扣回报的期望，他将未来的动作和状态的随机性都消除了。它依赖于当前的状态$s_t$、做出的动作$a_t$以及策略函数$\pi$，在这一步我们使用期望将状态的随机性消除，我们定义了状态价值函数$V_{\pi }$，它是动作价值函数对动作求期望。这样状态价值函数就只依赖于当前的状态$s_t$以及策略函数$\pi$

• 我们定义最优的动作价值函数为上面提到的$Q_{\pi }(s_t,a_t)$对策略函数$\pi$求最大化，它可以评价在状态s的情况下，做动作a的好坏。定义最优的状态价值函数为上面的到的$V_{\pi }(s)$对$\pi$求最大化，它可以告诉我们当前状态的好坏。这样我们就可以定义最优的优势函数$A^{\ast }(s,a)=Q^{\ast }(s,a)-V^{\ast }(s)$，它的意思就是将$V^{\ast }(s)$作为baseline，这样$A^{\ast }$就表示动作a相对于baseline的优势，动作a相对于baseline效果越好，$A^{\ast }$的值就越大。
  

Properties of Advantage Function

• 定理1：最优动作价值函数$Q^{\ast }(s,a)$关于动作a的最大值等于最优状态价值函数$V^{\ast }(s)$
• 回顾我们上面的到的$A^{\ast }(s,a)=Q^{\ast }(s,a)-V^{\ast }(s)$，同时对等式两边求最大化等式也成立，这样我们就可以得到$\underset{a}{\max }{A}^{\ast }(s,a)=\underset{a}{\max }{Q}^{\ast }(s,a)-V^{\ast }(s)$，上面定理1保证了$\underset{a}{\max }{Q}^{\ast }(s,a)=V^{\ast }(s)$，这样等式右边为0，故优势函数$A^{\ast }(s,a)$关于动作a的最大值为0.
  
• 将上面最优优势函数的定义转换一下就可以得到$Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)-\underset{a}{\max }{A}^{\ast }(s,a)$，前面我们得到$\underset{a}{\max }{A}^{\ast }(s,a)=0$，所以我们不妨在等式右边减去一个$\underset{a}{\max }{A}^{\ast }(s,a)$，
  

Dueling Network

Revisiting DQN

• DQN是神经网络对最优动作价值函数的近似
  

Approximating Advantage Function

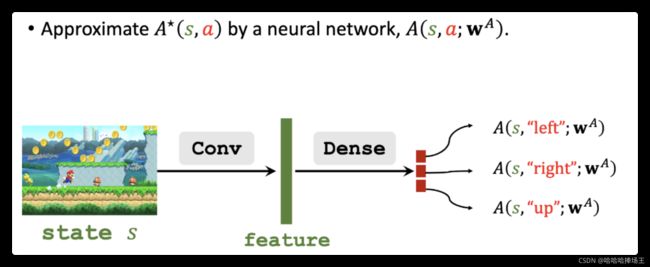
• 我们通过神经网络$A^{\ast }(s,a;w^A)$来近似$A^{\ast }(s,a)$，这里$w^A$是神经网络的参数，神经网络的结构和DQN是一样的。
  

Approximating State-Value Function

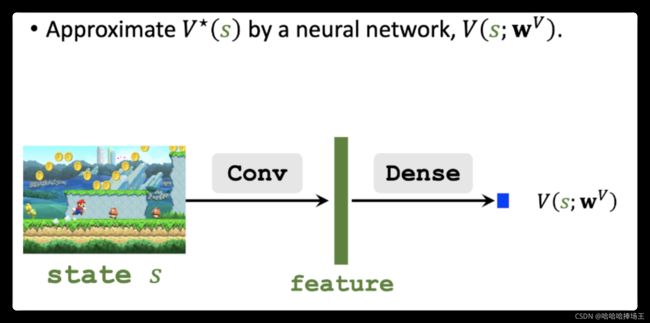
• 这里我们还需要一个神经网络来近似最优状态价值函数$V^{\ast }(s)$，这个神经网络的输入是状态s，这里输出是神经网络给状态s的打分。这里我们发现这个神经网络和上面的神经网络有相同的结构，真正实现的时候可以共享两个神经网络的参数。
  

Dueling Network：Formulation

• Theorem 2：$Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)-\underset{a}{\max }{A}^{\ast }(s,a)$
• 上面我们使用了两个神经网络分别近似了状态价值函数和优势函数，替换定理二中的来几个函数，可以得到$Q(s,a;w^A,w^V)$，它被称为Dueling Network。既然它是对动作价值函数的近似，那么它就和DQN有相同的作用，DQN有啥它就有啥，DQN怎么训练它就怎么训练。为了表示方便，后面使用w来表示它的参数。

Dueling Network

• 上面我们得到了Dueling Network的近似，它和DQN都是对动作价值函数的近似，所以它和DQN有相同的性质。

• 搭建Dueling Network：输入是状态s，使用一些卷积层来处理输入状态s，神经网络V和A共享卷积层参数。用一些全连接层得到的特征做变换得到一个输出向量，这个输出向量的元素对应优势函数给每个动作打的分数。使用一些全连接层将一个向量映射到一个实数，这个实数就是状态价值，表示当前状态的好坏。这样我们就得到了一个向量和一个实数，接下来我们使用这个实数和这个向量的每个元素分别相加，减去红色向量中的最大的元素，然后我们又可以得到一个向量，这个向量的大小和之前我们得到的向量是一样的，这个向量就是Dueling Network的最终的输出。输出的每一个元素对应了每个动作的价值，可以反映出动作的好坏。做决策的时候选出动作价值最大的动作，Agent执行这个动作。Dueling netwoek的输入和输出和DQN完全一样，功能也完全一样。

Training

• Dueling Network和DQN的输入和输出一样。
• 既然这里Dueling Network是对最优动作价值函数的近似，我们可以用Q-learning来训练Dueling Network，我们可以使用训练DQN的方式来训练Dueling Network。
  

Overcome Non-identifiability

• 看一下上面的两个等式，两个等式都是对的，我们证明过$\underset{a}{\max }(s,a)$恒等于0，那么我们干嘛要用等式2呢？原因是因为等式1有一个缺点，我们无法通过$Q^{\ast }$来唯一确定$V^{\ast }$和$A^{\ast }$。举例如下。这种不唯一性有什么危害呢？在上面Dueling Network的输出是通过$V^{\ast }+A^{\ast }$的到的，如果这两个值的波动绝对值相等，方向相反，那么毫无差别。但是两个神经网络都不稳定，这样的话就有危害了。这样加上对优势函数求最大化就可以更加稳定。但是实际操作中换成mean更加稳定，没有理论依据，就是实验效果好。
  

Summary