ZYNQ图像处理项目——线性神经网络识别mnist

一、线性神经网络识别mnist

线性神经网络其实也可以叫做线性分类器，其实就是没有激活函数的神经网络来对目标进行识别，像支持向量机、多元回归等都是线性的。这边我采用了线性神经网络来识别mnist数字。
我这边是看了一本讲神经网络的书籍，然后打算从线性神经网络入手，实现手写数字的识别。这本书真的讲的很通俗易懂，大家可以去看看，书名如下：

二、matlab训练mnist数据集

matlab的主要代码如下图所示，实现了mnist数据的读取、训练、测试和权重保存。这边不展开讲代码，matlab相关的代码我上传到资源了，大家如果想要看的就可以直接下载。

https://download.csdn.net/download/qq_40995480/87098176

clc;
% clear all;

Images = loadMNISTImages('./MNIST/t10k-images.idx3-ubyte');
Images = reshape(Images, 28, 28, []);
for i=1:10000
    Images(:,:,i) = Images(:,:,i)';
end
Images = reshape(Images, 784, 1, []);
Labels = loadMNISTLabels('./MNIST/t10k-labels.idx1-ubyte');
Labels(Labels == 0) = 10;    % 0 --> 10

rng(1);

W=1e-2*(2*rand(10,784)-1);

X = Images(:, :, 1:8000);
D = Labels(1:8000);

for epoch = 1:50
  epoch;
  [W] = MnistSoftmax(W, X, D);
end

% Test
X = Images(:, :, 8001:10000);
D = Labels(8001:10000);

acc = 0;
N   = length(D);
for k = 1:N
  x = X(:, :, k);                   % Input,           784x1
  v=W*x;
  y=softmax(v);

  [~, i] = max(y);
  if i == D(k)
    acc = acc + 1;
  end
end

%real test
number = imread('./MNIST/number9.bmp');
number=double(number)/15;
number=reshape(number,28,28);
number=number';
number=reshape(number,784,1);

v=W*number;
y=Softmax(v);

acc = acc / N;
fprintf('Accuracy is %f\n', acc);

save the W
W=W/max(max(W))*8191;
W=round(W);
save('weight.mat','W');

三、matlab实现线性神经网络

用训练好的权重系数进行书写数字识别，下面是matlab实现的代码，主要干的事情就是对图像的预处理、提取28*28的图像矩阵，之后利用权重与数据乘积来判断最大可能的数字。这部分代码大家也可以到我的资源下载。

https://download.csdn.net/download/qq_40995480/87098187

tic
clc;
clear all;

%read picture
%height and width
img_rgb=imread('./pic/number0.bmp');
h=size(img_rgb,1);
w=size(img_rgb,2);
%get rgb picture
figure(1);
subplot(121);
imshow(img_rgb);
title('rgb picture');
%get gray picture
% Relized method:myself Algorithm realized
% Y = ( R*77 + G*150 + B*29) >>8
% Cb = (-R*44 - G*84 + B*128) >>8
% Cr = ( R*128 - G*108 - B*20) >>8
img_rgb=double(img_rgb);
img_y=zeros(h,w);
img_u=zeros(h,w);
img_v=zeros(h,w);
for i = 1 : h
    for j = 1 : w
        img_y(i,j) = bitshift(( img_rgb(i,j,1)*77 + img_rgb(i,j,2)*150 + img_rgb(i,j,3)*29),-8);
        img_u(i,j) = bitshift((-img_rgb(i,j,1)*44 - img_rgb(i,j,2)*84 + img_rgb(i,j,3)*128 + 32678),-8);
        img_v(i,j) = bitshift(( img_rgb(i,j,1)*128 - img_rgb(i,j,2)*108 - img_rgb(i,j,3)*20 + 32678),-8);
    end
end
img_y = uint8(img_y); 
img_u = uint8(img_u); 
img_v = uint8(img_v); 
img_rgb = uint8(img_rgb);
subplot(122);
imshow(img_y);
title('gray picture');

%get bin picture
img_y=double(img_y);
img_thresh=zeros(h,w);
img_thresh_inverse=zeros(h,w);
THRESH_HOLD=150;
for i=1:h
   for j=1:w
       if(i>=384-56 && i<=384+55 && j>=512-56 && j<=512+55)
           if(img_y(i,j)>THRESH_HOLD)
               img_thresh(i,j)=255;
               img_thresh_inverse(i,j)=0;
           else 
               img_thresh(i,j)=0;
               img_thresh_inverse(i,j)=255;
           end
       else 
           img_thresh(i,j)=img_y(i,j);
           img_thresh_inverse(i,j)=img_y(i,j);
       end
   end
end
img_y=uint8(img_y);
img_thresh=uint8(img_thresh);
img_thresh_inverse=uint8(img_thresh_inverse);
figure(2);
subplot(121);
imshow(img_thresh);
title('bin picture');
subplot(122);
imshow(img_thresh_inverse);
title('bin inverse picture');

%open operation:corrosion and expansion
img_corrosion=zeros(h,w);
for i=1:h
   for j=1:w
       if(i>=384-56 && i<=384+55 && j>=512-56 && j<=512+55)
           a=img_thresh_inverse(i-1,j-1)&img_thresh_inverse(i-1,j)&img_thresh_inverse(i-1,j+1);
           b=img_thresh_inverse(i,j-1)&img_thresh_inverse(i,j)&img_thresh_inverse(i,j+1);
           c=img_thresh_inverse(i+1,j-1)&img_thresh_inverse(i+1,j)&img_thresh_inverse(i+1,j+1);
           if((a&b&c)==1)
               img_corrosion(i,j)=255;
           else 
               img_corrosion(i,j)=0;
           end
       else
               img_corrosion(i,j)=img_thresh_inverse(i,j);
       end
   end
end
img_corrosion=uint8(img_corrosion);
figure(3);
subplot(121);
imshow(img_corrosion);
title('corrosion picture');
img_expansion=zeros(h,w);
for i=1:h
   for j=1:w
       if(i>=384-55 && i<=384+54 && j>=512-55 && j<=512+54)
           a=img_corrosion(i-1,j-1)|img_corrosion(i-1,j)|img_corrosion(i-1,j+1);
           b=img_corrosion(i,j-1)|img_corrosion(i,j)|img_corrosion(i,j+1);
           c=img_corrosion(i+1,j-1)|img_corrosion(i+1,j)|img_corrosion(i+1,j+1);
           if((a|b|c)==1)
               img_expansion(i,j)=255;
           else 
               img_expansion(i,j)=0;
           end
       else
               img_expansion(i,j)=img_corrosion(i,j);
       end
   end
end
img_expansion=uint8(img_expansion);
subplot(122);
imshow(img_expansion);
title('expansion picture');

%get number matrix
test=imread('./pic/output_file1.bmp');
number=zeros(28,28);
for i=1:28
    for j=1:28
        number(i,j)=sum(sum(test(384-56+4*(i-1):384-56+4*i-1 , 512-56+4*(j-1):512-56+4*j-1)))/16;
    end
end
number=floor(number);
number=uint8(number);
pic=load('./pic/pic_28x28.txt');
pic=reshape(pic,28,28);
pic=pic';
pic=uint8(pic);
figure(4);
subplot(121);
imshow(number)
title('matlab number');
subplot(122);
imshow(pic)
title('vivado number');


%use softmax to recog the number
load('weight');
number=double(number);
number=number';
number=reshape(number,784,1);
v=W*number;
v=v/max(v)*10;
y=softmax(v);
n=0;
for i=1:10
   if(y(i)>=n)
       n=y(i);
       number_recog=i;
   end
   if(number_recog==10)
      number_recog=0; 
   end
end
fprintf('the probability is %f\n',n*100);
fprintf('the number is %d\n',number_recog);
toc

下面两张图是我测试的原始图像和转灰度之后的图像。

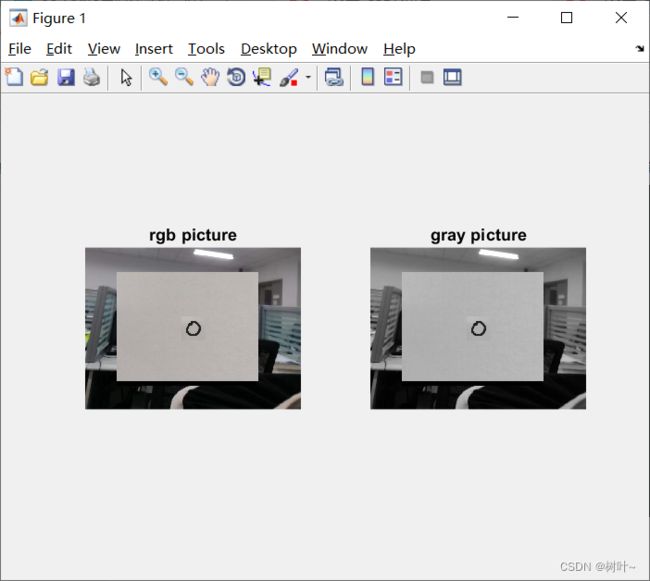
下图是将灰度图像对想要处理的区域(数字区域)进行二值化，之后在翻转。

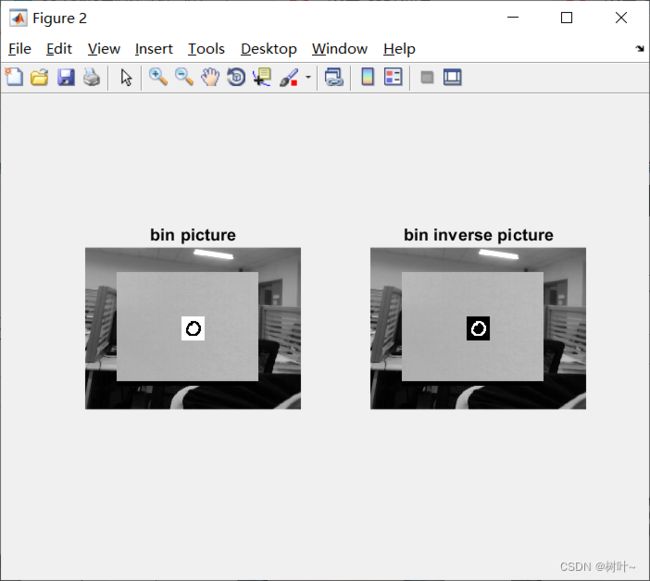
下面这两张图分别是我用matlab和vivado仿真提取得到的28*28的数据。

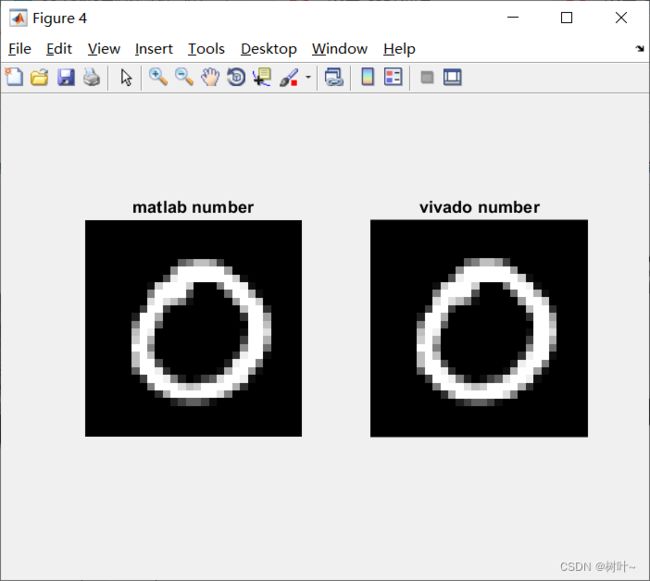
四、ZYNQ实现线性神经网络

关于ZYNQ实现神经网络的思路其实和matlab写的代码的思路是一样的，就是将其用verilog来实现而已，下图是我将线性神经网络部署到ZYNQ上实现的具体效果。在测试中发现，线性神经网络其实性能相较于卷积神经网络要差一点，下面工作会将激活函数、卷积层、池化层这些内容加进去，用ZYNQ来实现卷积神经网络。