指南：不平衡分类的成本敏感决策树（附代码&链接）

作者：Jason Brownlee 翻译：陈超 校对：冯羽

本文约3500字，建议阅读10+分钟

本文介绍了不平衡分类中的成本敏感决策树算法。

决策树算法对平衡分类是有效的，但在不平衡数据集上却表现不佳。

 

决策树分裂点是为了能够在最小混淆的情况下将所有实例分成两组。当两个组别分别都由其中一个类别的实例占主导，那么用于选择分裂点设置的标准即为合理，而事实上，少数类中的实例将会被忽略。

 

通过修改评估分裂点的标准并将每一类别的重要性均纳入考虑，即可解决这一问题，通常指的是加权的分裂点或者加权的决策树。

在本指南中，你将看到的是不平衡分类的加权决策树。

在学习完本指南之后，你将会了解：

• 标准决策树算法是怎样不支持不平衡分类的。

• 当选择分裂点时，决策树算法如何通过类权值对模型误差进行加权。

• 如何配置决策树算法中类的权值以及如何对不同的类权值配置进行网格化搜索。

SMOTE算法，单类别分类，成本敏感学习，阈值移动，以及更多其他内容，请检索我的新书，内含30个逐步教程以及完整的Python源代码。

新书链接：

https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification/

好的，我们开始。

如何对不平衡分类执行加权决策树

Photo by Bonnie Moreland, some rights reserved.

指南概观

本指南分为四部分，他们分别是：

一、不平衡分类数据集

二、不平衡分类决策树

三、Scikit-Learn中使用加权决策树

四、加权决策树的网格化搜索

一、不平衡分类数据集

在开始深入到不平衡分类的决策修正之前，我们先定义一个不平衡数据集。

我们可以使用 make_classification()函数来定义一个合成的不平衡两类别分类数据集。我们将生成10000个实例，其中少数类和多数类的比例为1:100。

make_classification()函数:

https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification/

...
# define dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
  n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=3)

一旦生成之后，我们可以总结类的分布来验证生成数据集是我们所期望的。

...
# summarize class distribution
counter = Counter(y)
print(counter)

最后，我们可以创造一个实例的散点图并依据类标签进行着色，来帮助我们理解该数据集中实例分类所面临的挑战。

...
# scatter plot of examples by class label
for label, _ in counter.items():
  row_ix = where(y == label)[0]
  pyplot.scatter(X[row_ix, 0], X[row_ix, 1], label=str(label))
pyplot.legend()
pyplot.show()

将这些代码整合在一起，生成合成数据集和绘制实例的完整示例。

# Generate and plot a synthetic imbalanced classification dataset
from collections import Counter
from sklearn.datasets import make_classification
from matplotlib import pyplot
from numpy import where
# define dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
  n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=3)
# summarize class distribution
counter = Counter(y)
print(counter)
# scatter plot of examples by class label
for label, _ in counter.items():
  row_ix = where(y == label)[0]
  pyplot.scatter(X[row_ix, 0], X[row_ix, 1], label=str(label))
pyplot.legend()
pyplot.show()

运行这个示例将会先创造一个数据集，然后汇总类的分布。

 

我们可以看到这个数据集接近1:100的类的分布，有比10000个稍微少一些的实例在多数类当中，100个实例在少数类中。

Counter({0: 9900, 1: 100})

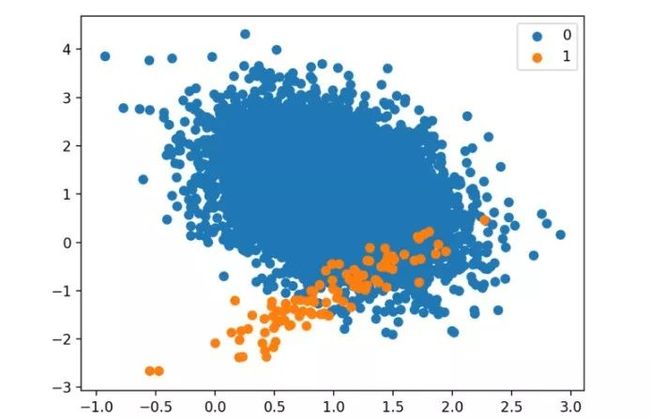
接下来，是数据集的散点图，该图展示了大量多数类（蓝色）的实例和少量少数类（橙色）的实例，其中有少许类的值重叠。

 

1:100类别不平衡性的两分类数据集散点图

接下来，我们可以在此数据集上拟合一个标准决策树模型。决策树可以使用scikit-learn工具包中的决策树分类器生成。

决策树分类器：

https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification/

...
# define model
model = DecisionTreeClassifier()

我们将使用重复交叉验证来评估此模型，共需三次重复的10层交叉验证。模型的性能将通过曲线下ROC面积(ROC AUC)在所有重复次以及全部层的均值获得。

10层交叉验证：

https://machinelearningmastery.com/k-fold-cross-validation/

...
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)
# summarize performance
print('Mean ROC AUC: %.3f' % mean(scores))

在不平衡分类问题上定义和评估一个标准决策树模型的完整实例如下。

 

决策树对二分类任务的有效模型，虽然他们本身对不平衡分类问题并不高效。

# fit a decision tree on an imbalanced classification dataset
from numpy import mean
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.tree import DecisionTreeClassifier
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
  n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=3)
# define model
model = DecisionTreeClassifier()
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)
# summarize performance
print('Mean ROC AUC: %.3f' % mean(scores)) 

运行该实例可评估标准决策树模型在不平衡数据集上的表现，并报告ROC AUC。

 

你的特定的结果可能会根据学习算法的固有随机性而变化。试着多运行几次。

 

我们可以看到这个模型能够实现ROC AUC大于0.5，并实现均值得分为0.746。

 

Mean ROC AUC: 0.746

这为任何标准决策树算法的改进提供了比较的基线。

 

二、不平衡分类决策树

决策树算法也被叫做分类和回归树（CART），包括生成树以及从训练集中分类实例。

分类和回归树：

https://machinelearningmastery.com/classification-and-regression-trees-for-machine-learning/

树可用于分离训练集，实例可以经由树的决策点到达叶节点并且被附上类标签。

 

树可以通过使用数据集中变量的值来分离训练集从而得到建构。在每一个点上，数据的分离以最贪心的方式使得最纯净的（最少混合的）实例组被选出来。

 

在这里，纯度意味着实例得到纯净地分离，由只包含0和只包含1的实例组成的类是最纯净的，50-50混合的类是最不纯的。常见的纯度通常由基尼不纯度来计算，虽然也可以通过信息熵（entropy）来计算。

信息熵：

https://machinelearningmastery.com/information-gain-and-mutual-information/

纯度测量包括计算一个给定类的实例被误分类的可能性。计算这些概率包括将每个组中每个类的实例数求和。

 

分离标准可以被更新，不仅是为了考虑分离的纯度，也是为了对每个类的重要性进行加权。

“我们导入成本敏感决策树的目的是为了修正与某一实例误分类的损失成比例的权重……”

-《一种导入损失敏感决策树的实例加权方法》,2002

https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification/

这可以通过加权和代替每一组别的实例数实现，这里系数被用于加权和。

 

更大的权重被分配给更重要的类，更小的权重则赋给不那么重要的类。

 

• 小权重：对节点纯度不那么重要，影响更低。

• 大权重：对节点纯度更重要，影响更高。

 

小权重可被分配给多数类，能够提升（降低）节点的纯度分数，否则这个节点

可能会看起来排序不那么好。这可能会使得更多来自多数类的实例被分到少数类里，并更好地适应少数类里的实例。

“更高的权值被分配给来自更高误分类成本的类当中的实例。”

-《从不平衡数据集中学习》，2018，第71页

https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification/

正因为如此，对决策树算法的这一修正被称为加权决策树，一个加权类的决策树，或者是成本敏感决策树。

 

分离点计算的修正是最常见的，虽然还有很多修正决策树建构算法以更好地适应类的不平衡的研究。

 

三、Scikit-Learn中使用加权决策树

Scikit-Learn Python 机器学习工具包提供了支持类加权的决策树算法的实现方法。

 

决策树算法提供了可被指定为模型超参数的class_weight参数。class_weight是一个定义每个类标签（例如，0和1）和应用到拟合模型时，决策树中分离组纯度计算权值的字典。

 

例如，一个对每个0和1类的1比1的权重可以作如下定义：

...
# define model
weights = {0:1.0, 1:1.0}
model = DecisionTreeClassifier(class_weight=weights)

类权值可有多种定义方式，例如：

• 领域专长：通过与学科专家交谈确定；

• 调参：通过例如网格化搜索的超参数搜索确定；

• 启发式：使用一般最佳实践确定。

使用类加权最好的实践是使用与训练集中的类分布的倒数。

 

例如，测试集类分布为少数类：多数类1:100的比例。该比例的倒数是1个多数类和100个少数类。例如：

...
# define model
weights = {0:1.0, 1:100.0}
model = DecisionTreeClassifier(class_weight=weights)

 

我们也可以使用分数定义同样的比例，并获得相同的结果。例如：

...
# define model
weights = {0:0.01, 1:1.0}
model = DecisionTreeClassifier(class_weight=weights)

 

启发式可以通过直接设置class_weight为'balanced'。例如：

...
# define model
model = DecisionTreeClassifier(class_weight='balanced')

我们可以通过使用在之前的部分定义的评估程序来对类加权的决策树算法进行评估。

 

我们期待类加权决策树的版本比没有类加权的标准决策树算法表现得更好。

 

完整的实例如下：

# decision tree with class weight on an imbalanced classification dataset
from numpy import mean
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.tree import DecisionTreeClassifier
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
  n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=3)
# define model
model = DecisionTreeClassifier(class_weight='balanced')
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate model
scores = cross_val_score(model, X, y, scoring='roc_auc', cv=cv, n_jobs=-1)
# summarize performance
print('Mean ROC AUC: %.3f' % mean(scores))

运行这一实例可以准备好合成的不平衡分类数据集，然后使用重复交叉验证评估类加权版的决策树算法。

 

你的结果可能会受到算法随机性的影响，尝试多运行几次。

 

ROC AUC的均值得分被报告，得到比未加权版本的决策树算法更好的得分：0.759比0.746。

 

Mean ROC AUC: 0.759

 

四、加权决策树的网格化搜索

使用训练集的倒数比的类加权是启发式的一种。

 

使用不同的类加权可能得到更好的表现，这也过分依赖于评估模型性能度量的选择。

 

在这一部分，我们将为加权决策树进行一系列不同类权重的网格化搜索并探索可得到最佳ROC AUC的结果。

 

我们将尝试下述对0类和1类的权重：

• 类0:100，类1:1；

• 类0:10，类1:1；

• 类0:1，类1:1；

• 类0:1，类1:100。

这些可被定义为GridSearchCV类的网格化搜索参数如下：

GridSearchCV类：

https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification/

...
# define grid
balance = [{0:100,1:1}, {0:10,1:1}, {0:1,1:1}, {0:1,1:10}, {0:1,1:100}]
param_grid = dict(class_weight=balance)

 

我们可以使用重复交叉验证对这些参数进行网格化搜索，并使用ROC AUC估计模型的表现：

...
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# define grid search
grid = GridSearchCV(estimator=model, param_grid=param_grid, n_jobs=-1, cv=cv, scoring='roc_auc')

一旦执行后，我们可以总结最佳配置，以及所有的结果如下：

...
# report the best configuration
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
# report all configurations
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print("%f (%f) with: %r" % (mean, stdev, param))

以下实例为不平衡数据集上的决策树算法，对五种不同的类权重进行网格化搜索。

 

我们可能会期待启发式类权重是最好的配置。

# grid search class weights with decision tree for imbalance classification
from numpy import mean
from sklearn.datasets import make_classification
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.tree import DecisionTreeClassifier
# generate dataset
X, y = make_classification(n_samples=10000, n_features=2, n_redundant=0,
  n_clusters_per_class=1, weights=[0.99], flip_y=0, random_state=3)
# define model
model = DecisionTreeClassifier()
# define grid
balance = [{0:100,1:1}, {0:10,1:1}, {0:1,1:1}, {0:1,1:10}, {0:1,1:100}]
param_grid = dict(class_weight=balance)
# define evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# define grid search
grid = GridSearchCV(estimator=model, param_grid=param_grid, n_jobs=-1, cv=cv, scoring='roc_auc')
# execute the grid search
grid_result = grid.fit(X, y)
# report the best configuration
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
# report all configurations
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print("%f (%f) with: %r" % (mean, stdev, param))

运行该实例使用重复k层交叉验证来评估每一个类权重，并报告最佳配置以及相关的平均ROC AUC得分。

 

你的结果可能会随着学习算法的随机性而变化，尝试多运行几次。

 

在这种情况下，我们可以看到1:100的多数：少数类比加权可以实现最佳的均值ROC得分。这与一般启发式的配置相匹配。

 

探索更严格的类权值来看其对ROC AUC均值得分的影响可能会很有趣。

 

Best: 0.752643 using {'class_weight': {0: 1, 1: 100}}
0.737306 (0.080007) with: {'class_weight': {0: 100, 1: 1}}
0.747306 (0.075298) with: {'class_weight': {0: 10, 1: 1}}
0.740606 (0.074948) with: {'class_weight': {0: 1, 1: 1}}
0.747407 (0.068104) with: {'class_weight': {0: 1, 1: 10}}
0.752643 (0.073195) with: {'class_weight': {0: 1, 1: 100}}

更多阅读

如果你想更深入了解，本部分提供了更多相关资源。

• 论文

• 《一种导入成本敏感决策树的实例加权方法》，2002.

  https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification/

• 书籍

• 《从不平衡数据中学习》，2018

  https://amzn.to/307Xlva

• 《不平衡学习：基础，算法和应用》，2013

  https://amzn.to/32K9K6d

• API

• sklearn.utils.class_weight.compute_class_weight API:

  https://scikit-learn.org/stable/modules/generated/sklearn.utils.class_weight.compute_class_weight.html

• sklearn.tree.DecisionTreeClassifier API:

  https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html

• sklearn.model_selection.GridSearchCV API:

  https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html

总结

在本指南中，你探索了不平衡分类的加权决策树。特别地，你学到了：

• 标准决策树算法怎样不支持不平衡分类；

• 当选择分裂点时，决策树算法如何通过类权值对模型误差进行加权；

• 如何配置决策树算法中类的权值以及如何对不同的类权值配置进行网格化搜索。

原文标题：

Cost-Sensitive Decision Trees for Imbalanced Classification

原文链接：

https://machinelearningmastery.com/cost-sensitive-decision-trees-for-imbalanced-classification

译者简介:陈超，北京大学应用心理硕士在读。本科曾混迹于计算机专业，后又在心理学的道路上不懈求索。越来越发现数据分析和编程已然成为了两门必修的生存技能，因此在日常生活中尽一切努力更好地去接触和了解相关知识，但前路漫漫，我仍在路上。

转自： 数据派THU 公众号；

END

版权声明：本号内容部分来自互联网，转载请注明原文链接和作者，如有侵权或出处有误请和我们联系。

合作请加QQ：365242293  

数据分析（ID : ecshujufenxi ）互联网科技与数据圈自己的微信，也是WeMedia自媒体联盟成员之一，WeMedia联盟覆盖5000万人群。