pytorch学习笔记（1）——Pytorch 在做什么

Pytorch 解决了什么问题

机器学习走上风口，男女老少都跃跃欲试。然而调用 GPU 、求导、卷积还是有一定门槛的。为了降低门槛，Pytorch 帮我们搬走了三座大山（Tensorflow 等也一样）：

1. 让运算能够在 GPU 上进行（速度可以接受了）
2. 让运算能够自动求导（代码更加简单了）
3. 让复杂运算能够直接调用（卷积不用自己写了）

Pytorch 是怎样设计的

在相互借（抄）鉴（袭）之后，大部分神经网络库都是这样搞的：

1. 封装一种新的数据结构（一般叫 Tensor ）
2. 重写 Numpy 中的运算使其能够在 GPU 上完成（一般用 CUDA ）
3. 实现运算的求导（一般是矩阵微分）
4. 实现运算组合的自动求导（一般基于计算图）

Pytorch 的使用

由于设计思路相似，大部分神经网络库都可以按以下思路使用：

1. 定义输入、输出
2. 定义参数
3. 输入、输出和参数之间进行运算得到损失函数
4. 求导获得参数的梯度
5. 更新参数

Tensorflow/Pytorch 的对比

我们按照上述思路拟合一条直线，Tensorflow 和 Pytroch 的实现步骤基本相同。

使用 Numpy 定义数据集：

# 定义数据集
batch_size = 100
in_dim = 1
train_x = np.linspace(1, 100, 100).reshape(batch_size, in_dim)
train_y = train_x * 3 + 5 + np.random.rand(1)

使用 Tensorflow 进行训练：

import numpy as np
import tensorflow as tf

# 定义数据集
learning_rate = 1e-6
batch_size = 100
in_dim = 1
out_dim = 1
train_x = np.linspace(1, 100, 100).reshape(batch_size, in_dim)
train_y = train_x * 3 + 5 + np.random.rand(1)

# 定义参数
W = tf.Variable(tf.random_uniform([in_dim, out_dim]))
b = tf.Variable(tf.zeros([out_dim]))

# 定义输入输出
x = tf.placeholder(tf.float32)
real_y = tf.placeholder(tf.float32)

# 得到损失函数
pre_y = tf.add(tf.matmul(x, W), b)
loss = tf.sqrt(tf.reduce_sum(tf.square(pre_y - real_y)))

# 自动求导并更新参数
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
# 可以理解为
# 求导
# W_grad, b_grad=tf.gradients(loss,[W,b])
# 更新参数
# W_update = W.assign(W - learning_rate * W_grad)
# b_update = b.assign(b - learning_rate * b_grad)

# 运行计算图
init = tf.initialize_all_variables()
with tf.Session() as sess:
    sess.run(init)
    for i in range(10000):
         _optimizer = sess.run([loss, optimizer], feed_dict={
            x: train_x,
            real_y: train_y
        })
        # 可以理解为
        # _, _ = sess.run([loss, W_update, b_update], feed_dict={
        #   x: train_x,
        #   real_y: train_y
        # })

使用 Pytorch 进行训练：

import numpy as np
import torch
from torch.autograd import Variable

# 定义数据集
learning_rate = 1e-6
batch_size = 100
in_dim = 1
out_dim = 1
train_x = np.linspace(1, 100, 100).reshape(batch_size, in_dim)
train_y = train_x * 3 + 5 + np.random.rand(1)

# 定义参数
W = Variable(torch.Tensor(in_dim, out_dim).uniform_(0, 1), requires_grad=True)
b = Variable(torch.zeros([out_dim]), requires_grad=True)

# 定义输入输出
x = Variable(torch.Tensor(train_x))
real_y = Variable(torch.Tensor(train_y))

for _ in range(10000):

  # 得到损失函数
  pre_y = torch.add(torch.mm(x, W), b)
  loss = torch.sqrt(torch.sum((pre_y - real_y).pow(2)))

  # 自动求导并更新参数
  loss.backward()
  
  with torch.no_grad():
    W -= learning_rate * W.grad
    b -= learning_rate * b.grad

    W.grad.zero_()
    b.grad.zero_()

我们在实际开发时的模型要复杂的多，因此并不会总是手动获取、更新参数。下文中我们会提到，如何将计算封装为一个层，定义前向和反向计算方式，以便利用优化求解器自动更新层中的所有参数。

基本使用

Tensor

Pytorch 将 Numpy 中的数组（包含同一数据类型的多维矩阵）封装为 Tensor，并提供了多种数据类型。我们可以使用 Tensor 将数组运算交给 GPU 负责。在 Pytorch 的实现中， Tensor 包含了矩阵的所有属性信息和一个指向数据块的指针：

1. size（形状）
2. stride（步长）
3. …
4. storage（数据块）

可以通过下面的代码获取 Storage 内的数据：

x = torch.Tensor([1, 2, 3])
x.storage()
# 1 2 3

Numpy 的封装

在使用时，可以将 Tensor 类比 ndarray。

Numpy	Pytorch
np.ndarray	torch.Tensor
np.float32	torch.float32
np.float64	torch.float64
np.int8	torch.int8
np.unit8	torch.unit8
np.int16	torch.int16
np.int32	torch.int32
np.int64	torch.int64

在 Pytorch 中构建矩阵和 Numpy 中完全相同。

numpy	pytorch
np.array([[0,1],[2,3]])	torch.tensor([[0,1],[2,3]])
np.array([[0,1],[2,3]], dtype=np.float32)	torch.tensor([[0,1],[2,3]], dtype=np.float32)

此外，Pytorch 为 Tensor 提供了大部分 Numpy 支持的构造函数。

numpy	pytorch
np.arange	torch.arange
np.linspace	torch.linspace
np.diag	torch.diag
np.tril	torch.tril
np.triu	torch.triu
np.copy	torch.copy

进行计算时 Pytorch 和 Numpy 完全相同。

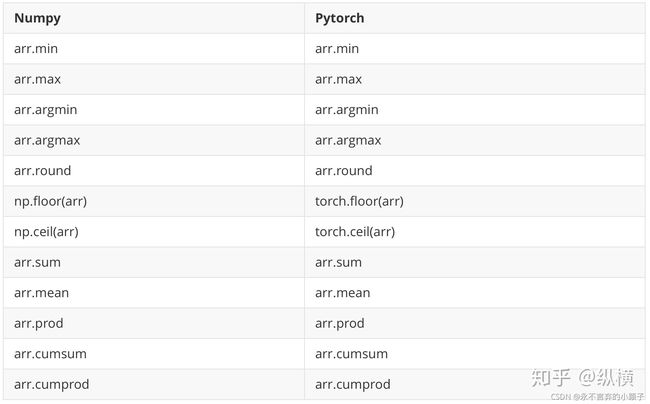
在计算过程中，默认的函数操作会创建一个新的 Tensor。如果想要改变一个 Tensor 的值，需要用函数名加下划线表示：

torch.abs(x) # 创建一个新的 Tensor
torch.abs_(x) # 改变 x

自动求导

torch.autograd.Variable 是进行运算和求导的单位，它包含了几个常用属性：

1. data – 保存数据，是一个 Tensor
2. grad – 保存导数，是一个与 data 形状一致的 Variable
3. creator – 用于实现常用计算，创建新的 Variable
4. grad_fn – 计算导数的方法

在对 Variable 进行运算时，运算会作用在 data 上，因此我们可以使用所有 Tensor 支持的方法进行运算。

使用 Variable 进行各种运算后，使用的 Variable 会被添加到计算图中，调用 backward 即可在 grad 上累加导数：

# 需要求导时必须传递 requires_grad=True
w = Variable(torch.Tensor([1.0,2.0,3.0]), requires_grad=True)
# 进行计算
result = torch.mean(w)
# 计算导数
result.backward()

# w.grad = [0.3333, 0.3333, 0.3333]

# 再次计算导数，此时会在上一次基础上累加
result.backward()

# w.grad = [0.6667, 0.6667, 0.6667]

# 如果不想累加需要手动清零
w.grad.data.zero_()
result.backward()

# w.grad = [0.3333, 0.3333, 0.3333]

作者：日知
链接：https://zhuanlan.zhihu.com/p/42584465
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

最优化

在获得梯度后，我们可以手动更新 Variable 中的 data：

learning_rate = 0.1
w.data.sub_(learning_rate * w.grad.data)

# 也可以使用重写的运算符
# w.data -= learning_rate * w.grad.data

如果在每次迭代中都需要手动调用函数计算梯度，进行参数更新，那么我们的代码将会过于复杂。Pytorch 像 Tensorflow 一样，为我们提供了优化求解器，帮助我们简化更新参数的操作。

import torch.optim as optim
# 创建优化求解器
optimizer = optim.SGD(net.parameters(), lr = 0.01)

for i in range(steps):
    optimizer.zero_grad() # 置零导数，原因见上一部分
    output = net(input)
    loss = criterion(output, target)
    loss.backward() # 计算导数
    optimizer.step() # 更新参数

常用层

所谓层，就是一组运算的集合。层提供了这组运算的正向和反向计算方法。其中，正向计算，接收输入数据，返回相应的输出数据。反向计算接收输出数据的梯度，返回输入数据的梯度。

1. nn.Sequential()

参数：若干个其他层
作用：将若干层组合在一起，方便结构显示

nn.Sequential(
    nn.Conv2d(in_dim, 6, 3, stride=1, padding=1),
    nn.ReLU(True),
    nn.MaxPool2d(2, 2),
    nn.Conv2d(6, 16, 5, stride=1, padding=0),
    nn.ReLU(True),
    nn.MaxPool2d(2, 2),
)

2. nn.Linear()

参数：输入和输出的维度
作用：全连接

nn.Linear(400, 120)

3. nn.Conv2d()

参数：输入的图片厚度、卷积核个数、卷积核大小、滑动步长和填充量
作用：卷积

nn.Conv2d(6, 16, 5, stride=1, padding=0)

4. nn.Relu()

参数：是否修改原对象
作用：激活函数

nn.ReLU(True)

5. nn.MaxPool2d

参数：池化窗口大小、滑动步长和填充量
作用：池化层

nn.MaxPool2d(2, 2)

6. 分类汇总

其他种类的层还有很多，第一次接触的同学可能不知道 Pytorch 提供了哪些层。这里将 Pytorch 提供的层分成 8 类进行展示。如果想了解某一个 API 的具体用法，可以查阅官方文档。

线性层：

nn.Linear(in_features, out_features, bias=True)
nn.Bilinear(in1_features, in2_features, out_features, bias=True)

激活层：

nn.ReLU(inplace=False)
nn.ReLU6(inplace=False)
nn.ELU(alpha=1.0, inplace=False)
nn.SELU(inplace=False)
nn.PReLU(num_parameters=1, init=0.25)
nn.LeakyReLU(negative_slope=0.01, inplace=False)
nn.Threshold(threshold, value, inplace=False)
nn.Hardtanh(min_val=-1, max_val=1, inplace=False, min_value=None, max_value=None)
nn.Sigmoid
nn.LogSigmoid
nn.Tanh
nn.Tanhshrink
nn.Softplus(beta=1, threshold=20)
nn.Softmax(dim=None)
nn.LogSoftmax(dim=None)
nn.Softmax2d
nn.Softmin(dim=None)
nn.Softshrink(lambd=0.5)
nn.Softsign

损失函数层：

nn.L1Loss(size_average=True, reduce=True)
nn.MSELoss(size_average=True, reduce=True)
nn.CrossEntropyLoss(weight=None, size_average=True, ignore_index=-100, reduce=True)
nn.NLLLoss(weight=None, size_average=True, ignore_index=-100, reduce=True)
nn.PoissonNLLLoss(log_input=True, full=False, size_average=True, eps=1e-08)
nn.NLLLoss2d(weight=None, size_average=True, ignore_index=-100, reduce=True)
nn.KLDivLoss(size_average=True, reduce=True)
nn.BCELoss(weight=None, size_average=True)
nn.BCEWithLogitsLoss(weight=None, size_average=True)
nn.MarginRankingLoss(margin=0, size_average=True)
nn.HingeEmbeddingLoss(margin=1.0, size_average=True)
nn.MultiLabelMarginLoss(size_average=True)
nn.SmoothL1Loss(size_average=True, reduce=True)
nn.SoftMarginLoss(size_average=True)
nn.CosineEmbeddingLoss(margin=0, size_average=True)

归一化层：

nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True)
nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)
nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True)
nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False)
nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False)
nn.InstanceNorm3d(num_features, eps=1e-05, momentum=0.1, affine=False)

卷积层：

nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
nn.ConvTranspose1d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)[s
nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)
nn.ConvTranspose3d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)

池化层：

nn.MaxPl1d(knl_iz, tid=Nn, padding=0, dilatin=1, tn_indi=Fal, il_md=Fal)
nn.MaxPl2d(knl_iz, tid=Nn, padding=0, dilatin=1, tn_indi=Fal, il_md=Fal)
nn.MaxPl3d(knl_iz, tid=Nn, padding=0, dilatin=1, tn_indi=Fal, il_md=Fal)
nn.Maxnpl1d(knl_iz, tid=Nn, padding=0)
nn.Maxnpl2d(knl_iz, tid=Nn, padding=0)
nn.Maxnpl3d(knl_iz, tid=Nn, padding=0)
nn.AvgPl1d(knl_iz, tid=Nn, padding=0, il_md=Fal, nt_inld_pad=T)
nn.AvgPl2d(knl_iz, tid=Nn, padding=0, il_md=Fal, nt_inld_pad=T)
nn.AvgPl3d(knl_iz, tid=Nn, padding=0, il_md=Fal, nt_inld_pad=T)
nn.FatinalMaxPl2d(knl_iz, tpt_iz=Nn, tpt_ati=Nn, tn_indi=Fal, _andm_ampl=Nn)
nn.LPPl2d(nm_typ, knl_iz, tid=Nn, il_md=Fal)
nn.AdaptivMaxPl1d(tpt_iz, tn_indi=Fal)
nn.AdaptivMaxPl2d(tpt_iz, tn_indi=Fal)
nn.AdaptivMaxPl3d(tpt_iz, tn_indi=Fal)
nn.AdaptivAvgPl1d(tpt_iz)
nn.AdaptivAvgPl2d(tpt_iz)
nn.AdaptivAvgPl3d(tpt_iz)

Dropout 层：

nn.Dropout(p=0.5, inplace=False)
nn.Dropout2d(p=0.5, inplace=False)
nn.Dropout3d(p=0.5, inplace=False)
nn.AlphaDropout(p=0.5)

距离函数层：

nn.CosineSimilarity(dim=1, eps=1e-08)
nn.PairwiseDistance(p=2, eps=1e-06)

自定义层

除了常用层，使用 Pytorch 还可以轻松地定制自定义层。相比与 Tensorflow 抽象层次更少，结构也更为清晰，十分容易上手。在上文中，我们提到“层就是一组运算的集合。层提供了这组运算的正向和反向计算方法。其中，正向计算，接收输入数据，返回相应的输出数据。反向计算接收输出数据的梯度，返回输入数据的梯度。”因此，我们在实现自定义层的时候，其实就是在实现正向和反向计算。

自定义层有两种方式：Function 和 Module。

Function 定义的层是无状态的，不保存和修改参数。

import torch
from torch.autograd import Function
 
class ReLU(Function)：
    # 正向计算
    def forward(self, input):
        self.save_for_backward(input)
 
        output = input.clamp(min=0)
        return output
    # 反向计算
    def backward(self, output_grad):
        input = self.to_save[0]
 
        input_grad = output_grad.clone()
        input_grad[input < 0] = 0
        return input_grad

Module 定义的层是有状态的，可以保存和修改参数。

class Linear(Module):
    def __init__(self, in_features, out_features, bias=True):
        super(Linear, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = Parameter(torch.Tensor(out_features, in_features))
        if bias:
            self.bias = Parameter(torch.Tensor(out_features))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        init.kaiming_uniform_(self.weight, a=math.sqrt(5))
        if self.bias is not None:
            fan_in, _ = init._calculate_fan_in_and_fan_out(self.weight)
            bound = 1 / math.sqrt(fan_in)
            init.uniform_(self.bias, -bound, bound)

    def forward(self, input):
        # 由 Function 实现
        return F.linear(input, self.weight, self.bias)

    def extra_repr(self):
        return 'in_features={}, out_features={}, bias={}'.format(
            self.in_features, self.out_features, self.bias is not None
        )

通常我们会用 Function 实现无状态的部分。

作者：日知
链接：https://zhuanlan.zhihu.com/p/42584465
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

import torch
from torch.autograd import Function
 
class Linear(Function):
 
     def forward(self, input, weight, bias=None):
         self.save_for_backward(input, weight, bias)
 
         output = torch.mm(input, weight.t())
         if bias is not None:
             output += bias.unsqueeze(0).expand_as(output)
 
         return output
 
     def backward(self, grad_output):
         input, weight, bias = self.saved_tensors
 
         grad_input = grad_weight = grad_bias = None
         if self.needs_input_grad[0]:
             grad_input = torch.mm(grad_output, weight)
         if self.needs_input_grad[1]:
             grad_weight = torch.mm(grad_output.t(), input)
         if bias is not None and self.needs_input_grad[2]:
             grad_bias = grad_output.sum(0).squeeze(0)
 
         if bias is not None:
             return grad_input, grad_weight, grad_bias
         else:
             return grad_input, grad_weight

封装模型

在常用层和自定义层的基础上，我们可以对模型进行封装。通常，我们是这样定义模型的：

1. 初始化时创建模型的所有层
2. 拼接所有层，实现前向计算方法（不需要定义反向，因为优化器会自动计算）
3. 定义损失函数
4. 调用优化器优化参数

例如，MNIST 手写体识别的卷积神经网络可以这样写：

# 定义模型
class CNN(nn.Module):
    def __init__(self, in_dim, n_class):
        super(Cnn, self).__init__()
        # 初始化卷积层
        self.conv_layers = nn.Sequential(
            nn.Conv2d(in_dim, 6, 3, stride=1, padding=1),
            nn.ReLU(True),
            nn.MaxPool2d(2, 2),
            nn.Conv2d(6, 16, 5, stride=1, padding=0),
            nn.ReLU(True),
            nn.MaxPool2d(2, 2),
        )
        # 初始化全连接层
        self.fc_layers = nn.Sequential(
            nn.Linear(400, 120),
            nn.Linear(120, 84),
            nn.Linear(84, n_class)
        )
 
    def forward(self, x):
        # 拼接层
        conv_out = self.conv(x)
        out = out.view(conv_out.size(0), -1)
        fc_out = self.fc(out)
        return fc_out
 
model = CNN(1, 10)
# GPU 加速
use_gpu = torch.cuda.is_available()
if use_gpu:
    model = model.cuda()
# 定义损失函数
criterion = nn.CrossEntropyLoss()
# 调用优化求解器求解
optimizer = optim.SGD(model.parameters(), lr=learning_rate)

链接：来源：知乎