世界坐标系/相机坐标系/图像坐标系 转换

一、各坐标系简要介绍

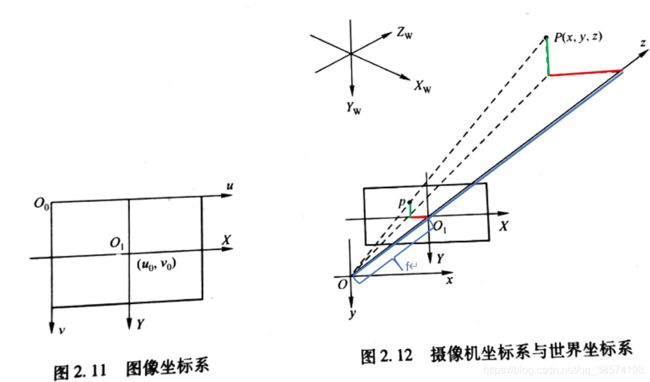
首先介绍数字图像处理领域中的图像坐标系，如上图左图所示，坐标系O_0为图像坐标系，其原点是在图像的左上角，每一个像素通过其所在位置的列数和行数索引 (u,v) 来表示。

另外需要建立图像坐标与物理单位的关系，而后才能将目标的真实世界坐标转换为图像坐标。即建立以物理单位表示的物理图像坐标系（有些文章将这个坐标系称为图像坐标系，而将数字图像中的坐标系称为像素坐标系，但是本文延续大多数把数字图像的坐标系称为图像坐标系的习惯，就把此坐标系称为物理图像坐标系），即上图左图中的坐标系O_1，其横纵轴用X,Y来标识，单位一般为mm（根据具体成像设备而定，不过单位不会影响坐标系的转换）。

再介绍世界坐标系与相机坐标系，如上图右图所示，坐标系O为相机坐标系，为一个3维坐标系，各维度分别用x,y,z表示，z轴称为摄像机光轴，与图像平面垂直，并且交点O_1为物理图像坐标系的原点。
上图右图左上角为世界坐标系，可以用来描述环境内的任何物体的位置，包括相机的位置，其各轴用X_w,Y_w,Z_w来标识。并且世界坐标系可以通过旋转与平移转换为相机坐标系。

二、坐标系转换

2.1 世界坐标系转为相机坐标系

点P为空间中的任一点，设其世界坐标系下的坐标为(X_w,Y_w,Z_w), 相机坐标系下的坐标为(x,y,z), 则可以通过相机坐标系与世界坐标系的关系可以由(X_w,Y_w,Z_w)计算(x,y,z):

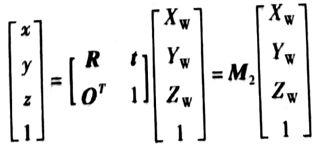
R, t 分别为3×3的旋转矩阵和3×1的平移向量。

2.2 相机坐标系转为物理图像坐标系

由第一节中图的右图所示，p为P在图像平面上的投影，设p的物理图像坐标为(X, Y), P的相机坐标系坐标为(x, y, z)，则根据比例关系得：

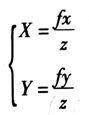
其中f为焦距，转为齐次坐标+矩阵形式为：

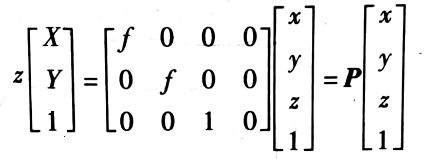
2.3 物理图像坐标系转为图像坐标系

设物理图像坐标系的原点在图像坐标系的位置为（u_0,v_0）（一般在图像的中心，不过有时候会存在偏差等）。对于物理图像坐标系中的任意一点(X,Y)都可以转换为图像坐标系中的坐标(u, v):

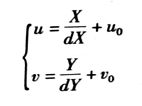
其中dX, dY 是成像元件的每个像素所对应的物理宽高，单位一般为mm。u_0, v_0, dX, dY 均为相机的固有参数。
通过齐次坐标将其写成矩阵形式：

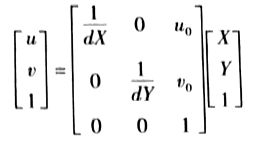
2.4 总结

结合上述公式即可以将任意一点的世界坐标转换为图像坐标：

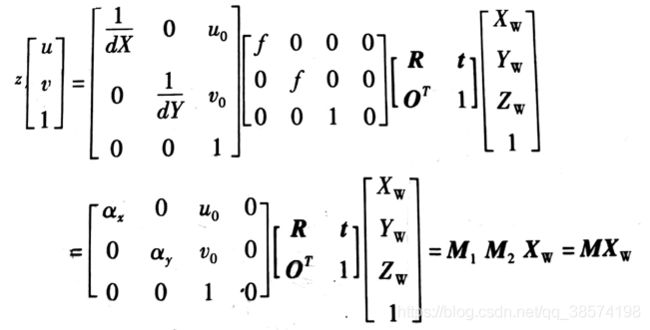
M1，M2分别仅与相机的内外参数相关。
由上式可知，当给出目标的世界坐标时，可以得到三个方程，消去z后可求得(u, v)
反之给出图像坐标(u, v)并不能求得其唯一的世界坐标，因为矩阵M为3×4维，不可逆，仅能解得一个射线方程，即该射线上的点投影均为(u, v)

2.5 为什么要使用齐次坐标

（个人思考）
假如不使用齐次坐标的话，物理图像坐标系转为图像坐标系的矩阵将为2×3维，而相机坐标系转物理图像坐标系的矩阵变为2×3维，这两个矩阵分别为2.4节公式第一行等号右边的前两个矩阵，可以看出，不使用齐次坐标的话矩阵无法相乘，那就无法完成坐标转换。

参考文献

《机器视觉理论及应用》 电子工业出版社

本文仅为本人学习过程中的笔记以及一些个人思考，文中如有错误的地方还请指正