理解droupout

本文主要介绍Dropout及延伸下来的一些方法，以便更深入的理解。

想要提高CNN的表达或分类能力，最直接的方法就是采用更深的网络和更多的神经元，即deeper and wider。但是，复杂的网络也意味着更加容易过拟合。于是就有了Dropout，大部分实验表明其具有一定的防止过拟合的能力。

1- Dropout

最早的Dropout可以看Hinton的这篇文章 
《Improving neural networks by preventing co-adaptation of feature Detectors》

从文章的名字我们就可以先对Dropout的工作原理有个猜测：过拟合意味着网络记住了训练样本，而打破网络固定的工作方式，就有可能打破这种不好的记忆。

Ok，我们直接来看什么是Dropout：

需要注意的是：论文中Dropout被使用在全连接层之后，而目前的caffe框架中，其可以使用在各种层之后。

如上图左，为没有Dropout的普通2层全连接结构，记为 r=a(Wv)，其中a为激活函数。

如上图右，为在第2层全连接后添加Dropout层的示意图。即在 模 型 训 练 时 随机让网络的某些节点不工作（输出置0），其它过程不变。

对于Dropout这样的操作为何可以防止训练过拟合，原作者也没有给出数学证明，只是有一些直观的理解或者说猜想。下面说几个我认为比较靠谱的解释：

(1) 由于随机的让一些节点不工作了，因此可以避免某些特征只在固定组合下才生效，有意识地让网络去学习一些普遍的共性（而不是某些训练样本的一些特性）

(2) Bagging方法通过对训练数据有放回的采样来训练多个模型。而Dropout的随机意味着每次训练时只训练了一部分，而且其中大部分参数还是共享的，因此和Bagging有点相似。因此，Dropout可以看做训练了多个模型，实际使用时采用了模型平均作为输出 
（具体可以看一下论文，论文讲的不是很明了，我理解的也够呛）

训练的时候，我们通常设定一个dropout ratio = p,即每一个输出节点以概率 p 置0(不工作)。假设每一个输出都是相互独立的，每个输出都服从二项伯努利分布B(1-p)，则大约认为训练时 只使用了 (1-p)比例的输出。

测试的时候，最直接的方法就是保留Dropout层的同时，将一张图片重复测试M次，取M次结果的平均作为最终结果。假如有N个节点，则可能的情况为R=2^N,如果M远小于R，则显然平均效果不好；如果M≈N，那么计算量就太大了。因此作者做了一个近似：可以直接去掉Dropout层，将所有输出 都使用 起来，为此需要将尺度对齐，即比例缩小输出 r=r*(1-p)。 
即如下公式： 
 
特别的， 为了使用方便，我们不在测试时再缩小输出，而在训练时直接将输出放大1/(1-p)倍。

结论： Dropout得到了广泛的使用，但具体用到哪里、训练一开始就用还是后面才用、dropout_ratio取多大，还要自己多多尝试。有时添加Dropout反而会降低性能。

2- DropConnect

DropConnect来源于《Regularization of Neural Networks using DropConnect》这篇文章。

更详细的实验对比以及代码，可以点击http://cs.nyu.edu/~wanli/dropc/

该方法改进于第一节介绍的Dropout,具体可看下图作对比 

由图可知，二者的区别很明显：Dropout是将输出随机置0，而DropConnect是将权重随机置0。 
文章说之所以这么干是因为原来的Dropout进行的不够充分，随机采样不够合理。这可以从下图进行理解： 

如上图所示，a表示不加任何Drop时的一层网络模型。添加Drop相当于给权重再乘以一个随机掩膜矩阵M。

不同的是，DropConnect由于直接对权重随机置0，因此其掩膜显得更加具有随机性，如b所示。而Dropout仅对输出进行随机置0,因此其掩膜相当于是对随机的行和列进行置0，如c所示。

训练的时候，训练过程与Dropout基本相同。

测试的时候，我们同样需要一种近似的方法。如下图公式所示： 
 
注意： 掩膜矩阵M的每一个元素都满足二项伯努利分布。假如M的维度为m*n，则可能的掩膜有2^(m*n)种，之前提到过我们可以粗暴的遍历所有的掩膜然后计算结果最后求平均。中心极限定理：和分布渐进于正态分布。 于是，我们可以不去遍历，而是通过计算每一维的均值与方差，确定每一维的正态分布，最后在此正态分布上做多次采样后求平均即可获得最终的近似结果。

具体测试时的算法流程如下： 
 
其中，Z是在正态分布上的采样次数，一般来说越大越好，但会使得计算变慢。

实验： 作者当然要做很多对比试验，但其实发现效果并不比Dropout优秀太多，反而计算量要大很多，因此到目前DropConnect并没有得到广泛的应用。具体的对比，可以参看原文，这里我只贴一张图来说明对于Drop ratio的看法： 
 
由此可以看出，drop ratio并不是越大越好，具体需要大家多做实验多体会。

3- 未完待续

dropout layer的目的是为了防止CNN 过拟合。那么为什么可以有效的防止过拟合呢？

首先，想象我们现在只训练一个特定的网络，当迭代次数增多的时候，可能出现网络对训练集拟合的很好（在训练集上loss很小），但是对验证集的拟合程度很差的情况。所以，我们有了这样的想法：可不可以让每次跌代随机的去更新网络参数（weights），引入这样的随机性就可以增加网络generalize 的能力。所以就有了dropout 。

在训练的时候，我们只需要按一定的概率（retaining probability）p 来对weight layer 的参数进行随机采样，将这个子网络作为此次更新的目标网络。可以想象，如果整个网络有n个参数，那么我们可用的子网络个数为 2^n 。 并且，当n很大时，每次迭代更新 使用的子网络基本上不会重复，从而避免了某一个网络被过分的拟合到训练集上。

那么测试的时候怎么办呢？ 一种最naive的方法是，我们把 2^n 个子网络都用来做测试，然后以某种 voting 机制将所有结果结合一下（比如说平均一下下），然后得到最终的结果。但是，由于n实在是太大了，这种方法实际中完全不可行！ 

所以有人提出，那我做一个大致的估计不就得了，我从2^n个网络中随机选取 m 个网络做测试，最后在用某种voting 机制得到最终的预测结果。这种想法当然可行，当m很大时但又远小于2^n时，能够很好的逼近原2^n个网络结合起来的预测结果。但是，有没有更好的办法呢？ of course！那就是dropout 自带的功能，能够通过一次测试得到逼近于原2^n个网络组合起来的预测能力！ 

虽然训练的时候我们使用了dropout， 但是在测试时，我们不使用dropout （不对网络的参数做任何丢弃，这时dropout layer相当于进来什么就输出什么）。然后，把测试时dropout layer的输出乘以训练时使用的retaining probability  p （这时dropout layer相当于把进来的东东乘以p）。仔细想想这里面的意义在哪里呢？？？ 事实上，由于我们在测试时不做任何的参数丢弃，如上面所说，dropout layer 把进来的东西原样输出，导致在统计意义下，测试时 每层 dropout layer的输出比训练时的输出多加了【（1 - p）*100】%  units 的输出。 即 【p*100】% 个units 的和  是同训练时随机采样得到的子网络的输出一致，另【（1 - p）*100】%  的units的和  是本来应该扔掉但是又在测试阶段被保留下来的。所以，为了使得dropout layer 下一层的输入和训练时具有相同的“意义”和“数量级”，我们要对测试时的伪dropout layer的输出（即下层的输入）做 rescale： 乘以一个p，表示最后的sum中只有这么大的概率，或者这么多的部分被保留。这样以来，只要一次测试，将原2^n个子网络的参数全部考虑进来了，并且最后的 rescale 保证了后面一层的输入仍然符合相应的物理意义和数量级。

假设x是dropout layer的输入，y是dropout layer的输出，W是上一层的所有weight parameters， 是以retaining probability 为p 采样得到的weight parameter子集。把上面的东西用公式表示（忽略bias）：

train：  

test:

但是一般写程序的时候，我们想直接在test时用   ， 这种表达式。（where  ） 

因此我们就在训练的时候就直接训练  。 所以训练时，第一个公式修正为    。 即把dropout的输入乘以p 再进行训练，这样得到的训练得到的weight 参数就是  ，测试的时候除了不使用dropout外，不需要再做任何rescale。Caffe 和Lasagne 里面的代码就是这样写的。

参考文献： Improving Neural Networks with Dropout， Hinton学生的一片thesis

       Dropout: A Simple Way to Prevent Neural Networks from Overfitting

组合派

参考文献中第一篇中的观点，Hinton老大爷提出来的，关于Hinton在深度学习界的地位我就不再赘述了，光是这地位，估计这一派的观点就是“武当少林”了。注意，派名是我自己起的，各位勿笑。

观点

该论文从神经网络的难题出发，一步一步引出dropout为何有效的解释。大规模的神经网络有两个缺点：

• 费时
• 容易过拟合

这两个缺点真是抱在深度学习大腿上的两个大包袱，一左一右，相得益彰，额不，臭气相投。过拟合是很多机器学习的通病，过拟合了，得到的模型基本就废了。而为了解决过拟合问题，一般会采用ensemble方法，即训练多个模型做组合，此时，费时就成为一个大问题，不仅训练起来费时，测试起来多个模型也很费时。总之，几乎形成了一个死锁。

Dropout的出现很好的可以解决这个问题，每次做完dropout，相当于从原始的网络中找到一个更瘦的网络，如下图所示：

因而，对于一个有N个节点的神经网络，有了dropout后，就可以看做是2ⁿ个模型的集合了，但此时要训练的参数数目却是不变的，这就解脱了费时的问题。

动机论

虽然直观上看dropout是ensemble在分类性能上的一个近似，然而实际中，dropout毕竟还是在一个神经网络上进行的，只训练出了一套模型参数。那么他到底是因何而有效呢？这就要从动机上进行分析了。论文中作者对dropout的动机做了一个十分精彩的类比：

在自然界中，在中大型动物中，一般是有性繁殖，有性繁殖是指后代的基因从父母两方各继承一半。但是从直观上看，似乎无性繁殖更加合理，因为无性繁殖可以保留大段大段的优秀基因。而有性繁殖则将基因随机拆了又拆，破坏了大段基因的联合适应性。

但是自然选择中毕竟没有选择无性繁殖，而选择了有性繁殖，须知物竞天择，适者生存。我们先做一个假设，那就是基因的力量在于混合的能力而非单个基因的能力。不管是有性繁殖还是无性繁殖都得遵循这个假设。为了证明有性繁殖的强大，我们先看一个概率学小知识。

比如要搞一次恐怖袭击，两种方式： 
- 集中50人，让这50个人密切精准分工，搞一次大爆破。 
- 将50人分成10组，每组5人，分头行事，去随便什么地方搞点动作，成功一次就算。

哪一个成功的概率比较大？ 显然是后者。因为将一个大团队作战变成了游击战。

那么，类比过来，有性繁殖的方式不仅仅可以将优秀的基因传下来，还可以降低基因之间的联合适应性，使得复杂的大段大段基因联合适应性变成比较小的一个一个小段基因的联合适应性。

dropout也能达到同样的效果，它强迫一个神经单元，和随机挑选出来的其他神经单元共同工作，达到好的效果。消除减弱了神经元节点间的联合适应性，增强了泛化能力。

个人补充一点：那就是植物和微生物大多采用无性繁殖，因为他们的生存环境的变化很小，因而不需要太强的适应新环境的能力，所以保留大段大段优秀的基因适应当前环境就足够了。而高等动物却不一样，要准备随时适应新的环境，因而将基因之间的联合适应性变成一个一个小的，更能提高生存的概率。

dropout带来的模型的变化

而为了达到ensemble的特性，有了dropout后，神经网络的训练和预测就会发生一些变化。

• 训练层面

  无可避免的，训练网络的每个单元要添加一道概率流程。 
  

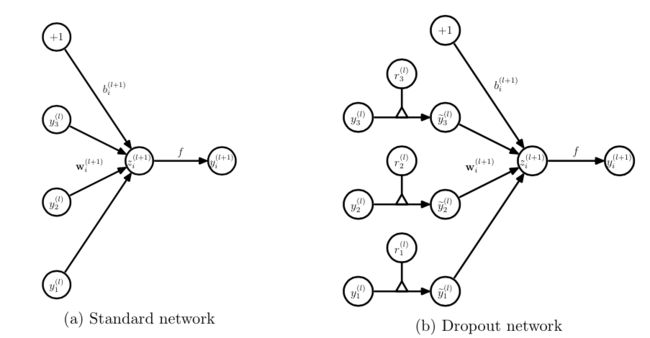
  对应的公式变化如下如下：

  • 没有dropout的神经网络 
    
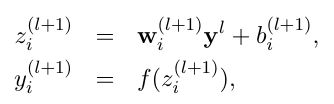
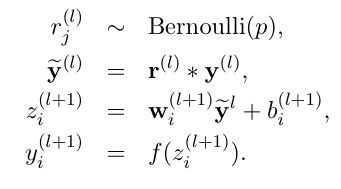
  • 有dropout的神经网络 
    

• 测试层面

  预测的时候，每一个单元的参数要预乘以p。 
  

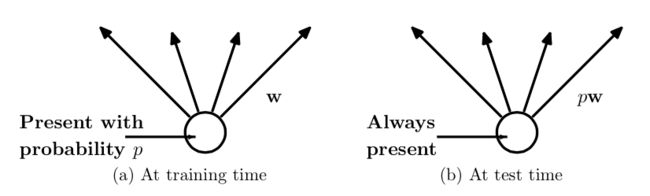
论文中的其他技术点

• 防止过拟合的方法：

  • 提前终止（当验证集上的效果变差的时候）
  • L1和L2正则化加权
  • soft weight sharing
  • dropout

• dropout率的选择

  • 经过交叉验证，隐含节点dropout率等于0.5的时候效果最好，原因是0.5的时候dropout随机生成的网络结构最多。
  • dropout也可以被用作一种添加噪声的方法，直接对input进行操作。输入层设为更接近1的数。使得输入变化不会太大（0.8）

• 训练过程

  • 对参数w的训练进行球形限制(max-normalization)，对dropout的训练非常有用。
  • 球形半径c是一个需要调整的参数。可以使用验证集进行参数调优
  • dropout自己虽然也很牛，但是dropout、max-normalization、large decaying learning rates and high momentum组合起来效果更好，比如max-norm regularization就可以防止大的learning rate导致的参数blow up。
  • 使用pretraining方法也可以帮助dropout训练参数，在使用dropout时，要将所有参数都乘以1/p。

• 部分实验结论

  该论文的实验部分很丰富，有大量的评测数据。

  • maxout 神经网络中得另一种方法，Cifar-10上超越dropout

  • 文本分类上，dropout效果提升有限，分析原因可能是Reuters-RCV1数据量足够大，过拟合并不是模型的主要问题

  • dropout与其他standerd regularizers的对比 
    
    • L2 weight decay
    • lasso
    • KL-sparsity
    • max-norm regularization
    • dropout
  • 特征学习 
    
    • 标准神经网络，节点之间的相关性使得他们可以合作去fix其他节点中得噪声，但这些合作并不能在unseen data上泛化，于是，过拟合，dropout破坏了这种相关性。在autoencoder上，有dropout的算法更能学习有意义的特征（不过只能从直观上，不能量化）。
    • 产生的向量具有稀疏性。
    • 保持隐含节点数目不变，dropout率变化；保持激活的隐节点数目不变，隐节点数目变化。
  • 数据量小的时候，dropout效果不好，数据量大了，dropout效果好

  • 模型均值预测

    • 使用weight-scaling来做预测的均值化
    • 使用mente-carlo方法来做预测。即对每个样本根据dropout率先sample出来k个net，然后做预测，k越大，效果越好。

  • Multiplicative Gaussian Noise 
    使用高斯分布的dropout而不是伯努利模型dropout

  • dropout的缺点就在于训练时间是没有dropout网络的2-3倍。

进一步需要了解的知识点

• dropout RBM
• Marginalizing Dropout 
  具体来说就是将随机化的dropout变为确定性的，比如对于Logistic回归，其dropout相当于加了一个正则化项。
• Bayesian neural network对稀疏数据特别有用，比如medical diagnosis, genetics, drug discovery and other computational biology applications

噪声派

参考文献中第二篇论文中得观点，也很强有力。

观点

观点十分明确，就是对于每一个dropout后的网络，进行训练时，相当于做了Data Augmentation，因为，总可以找到一个样本，使得在原始的网络上也能达到dropout单元后的效果。 比如，对于某一层，dropout一些单元后，形成的结果是(1.5,0,2.5,0,1,2,0)，其中0是被drop的单元，那么总能找到一个样本，使得结果也是如此。这样，每一次dropout其实都相当于增加了样本。

稀疏性

知识点A

首先，先了解一个知识点：

When the data points belonging to a particular class are distributed along a linear manifold, or sub-space, of the input space, it is enough to learn a single set of features which can span the entire manifold. But when the data is distributed along a highly non-linear and discontinuous manifold, the best way to represent such a distribution is to learn features which can explicitly represent small local regions of the input space, effectively “tiling” the space to define non-linear decision boundaries.

大致含义就是： 
在线性空间中，学习一个整个空间的特征集合是足够的，但是当数据分布在非线性不连续的空间中得时候，则学习局部空间的特征集合会比较好。

知识点B

假设有一堆数据，这些数据由M个不同的非连续性簇表示，给定K个数据。那么一个有效的特征表示是将输入的每个簇映射为特征以后，簇之间的重叠度最低。使用A来表示每个簇的特征表示中激活的维度集合。重叠度是指两个不同的簇的A_i和A_j之间的Jaccard相似度最小，那么：

• 当K足够大时，即便A也很大，也可以学习到最小的重叠度
• 当K小M大时，学习到最小的重叠度的方法就是减小A的大小，也就是稀疏性。

上述的解释可能是有点太专业化，比较拗口。主旨意思是这样，我们要把不同的类别区分出来，就要是学习到的特征区分度比较大，在数据量足够的情况下不会发生过拟合的行为，不用担心。但当数据量小的时候，可以通过稀疏性，来增加特征的区分度。

因而有意思的假设来了，使用了dropout后，相当于得到更多的局部簇，同等的数据下，簇变多了，因而为了使区分性变大，就使得稀疏性变大。

为了验证这个数据，论文还做了一个实验，如下图：

该实验使用了一个模拟数据，即在一个圆上，有15000个点，将这个圆分为若干个弧，在一个弧上的属于同一个类，一共10个类，即不同的弧也可能属于同一个类。改变弧的大小，就可以使属于同一类的弧变多。

实验结论就是当弧长变大时，簇数目变少，稀疏度变低。与假设相符合。

个人观点：该假设不仅仅解释了dropout何以导致稀疏性，还解释了dropout因为使局部簇的更加显露出来，而根据知识点A可得，使局部簇显露出来是dropout能防止过拟合的原因，而稀疏性只是其外在表现。

论文中的其他技术知识点

• 将dropout映射回得样本训练一个完整的网络，可以达到dropout的效果。
• dropout由固定值变为一个区间，可以提高效果
• 将dropout后的表示映射回输入空间时，并不能找到一个样本x^*使得所有层都能满足dropout的结果，但可以为每一层都找到一个样本，这样，对于每一个dropout，都可以找到一组样本可以模拟结果。

• dropout对应的还有一个dropConnect，公式如下：

  • dropout

    

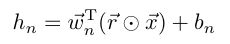
  • dropConnect

    

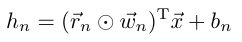
• 试验中，纯二值化的特征的效果也非常好，说明了稀疏表示在进行空间分区的假设是成立的，一个特征是否被激活表示该样本是否在一个子空间中。

参考文献

[1]. Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958.

[2]. Dropout as data augmentation. http://arxiv.org/abs/1506.08700