Numpy实现全连接神经网络并可视化训练过程
1. 模型
1.1 前向传播
对于每一层网络有
Y i = W i T Z i − 1 + b i Z i = g ( Y i ) 其中: Y i − > ( n i , s ) , W i − > ( n i − 1 , n i ) , b i − > ( n i , 1 ) , Z i − > ( n i , s ) n i 为第 i 层的神经元个数, s 为样本数 \begin{align*} Y_i &= W_i^TZ_{i-1}+b_i \\ Z_i&=g(Y_i) \\ 其中:Y_i->(n^i,s)&,W_i->(n^{i-1},n^i),b_i->(n^i,1),Z_i->(n^i,s)\\ n^i&为第i层的神经元个数,s为样本数 \end{align*} YiZi其中:Yi−>(ni,s)ni=WiTZi−1+bi=g(Yi),Wi−>(ni−1,ni),bi−>(ni,1),Zi−>(ni,s)为第i层的神经元个数,s为样本数
1.2 激活函数及其导数
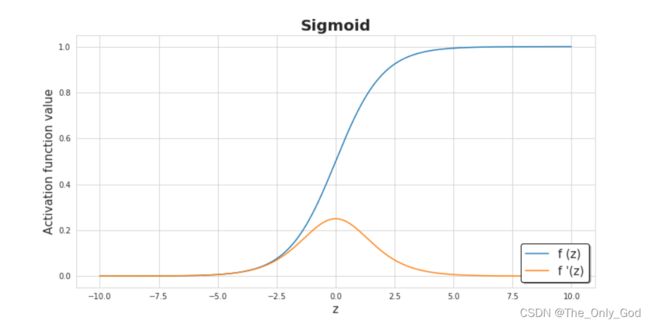
1.2.1 Sigmoid
g ( y ) = 1 1 + e − y g ′ ( y ) = g ( y ) ( 1 − g ( y ) ) \begin{align*} g(y)&=\frac{1}{1+e^{-y}} \\ g'(y)&=g(y)(1-g(y)) \end{align*} g(y)g′(y)=1+e−y1=g(y)(1−g(y))
1.2.2 ReLU
g ( y ) = { y y > 0 0 y < = 0 g ′ ( y ) = { 1 y > 0 0 y < = 0 \begin{align*} g(y)=\begin{cases} y & y>0 \\ 0 & y<=0 \end{cases} \\ g'(y)=\begin{cases} 1 & y>0 \\ 0 & y<=0 \end{cases} \end{align*} g(y)={y0y>0y<=0g′(y)={10y>0y<=0
1.3 损失函数及其导数
本文采用的是二元交叉熵损失函数
l o s s s u m = − ∑ y i = 1 s [ y i l o g ( p i ) + ( 1 − y i ) l o g ( 1 − p i ) ] l o s s = − [ y i l o g ( p i ) + ( 1 − y i ) l o g ( 1 − p i ) ] l o s s ′ = − ( y i p i + 1 − y i 1 − p i ) \begin{align*} loss_{sum}&=-\sum_{y_i=1}^s[y_ilog(p_i)+(1-y_i)log(1-p_i)] \\ loss&=-[y_ilog(p_i)+(1-y_i)log(1-p_i)] \\ loss'&=-(\frac{y_i}{p_i}+\frac{1-y_i}{1-p_i}) \end{align*} losssumlossloss′=−yi=1∑s[yilog(pi)+(1−yi)log(1−pi)]=−[yilog(pi)+(1−yi)log(1−pi)]=−(piyi+1−pi1−yi)
1.4 反向传播
d Z i = ∂ L ∂ Z i , d Y i = ∂ L ∂ Y i , d W i = ∂ L ∂ W i , d b i = ∂ L ∂ b i dZ_i=\frac{\partial L}{\partial Z_i},dY_i=\frac{\partial L}{\partial Y_i},dW_i=\frac{\partial L}{\partial W_i},db_i=\frac{\partial L}{\partial b_i} dZi=∂Zi∂L,dYi=∂Yi∂L,dWi=∂Wi∂L,dbi=∂bi∂L
d W i = 1 s Z i − 1 × d Y i T d b i = 1 s ∑ j s d Y i , j d Y i = d Z i g ′ ( Y i ) d Z i − 1 = W i × d Y i 其中: d W i − > ( n i − 1 , n i ) , d b i − > ( b i , 1 ) , d Z i − > ( n i , 1 ) , d Y i − > ( n i , 1 ) \begin{align*} dW_i &= \frac{1}{s}Z_{i-1}\times dY_i^T \\ db_i &= \frac{1}{s}\sum_j^s dY_{i,j} \\ dY_i&=dZ_ig'(Y_i)\\ dZ_{i-1}&=W_i\times dY_i\\ 其中:dW_i->(n^{i-1},n^i),&db_i->(b^i,1),dZ_i->(n^i,1),dY_i->(n^i,1) \end{align*} dWidbidYidZi−1其中:dWi−>(ni−1,ni),=s1Zi−1×dYiT=s1j∑sdYi,j=dZig′(Yi)=Wi×dYidbi−>(bi,1),dZi−>(ni,1),dYi−>(ni,1)
反向传播理解难点:
- 所有样本同时求反向传播、具体到某个微分是为所有样本计算所得微分的平均值
- 隐藏层具体某个神经元的单个样本的 d Z i − 1 , j = ∑ k = 1 n i W i , j , k × d Z i , k dZ_{i-1,j}=\sum_{k=1}^{n^i}W_{i,j,k}\times dZ_{i,k} dZi−1,j=∑k=1niWi,j,k×dZi,k
2. 源码
项目结构
- tools
- activation.py
- loss.py
- visualize.py
- MLP.py
2.1 tool包
主要包含激活函数、损失函数和训练过程可视化
2.1.1 activation.py
import numpy as np
def sigmoid(y):
return 1 / (1 + np.exp(-y))
def sigmoid_backwrad(dz, y):
sig = sigmoid(y)
return dz * sig * (1 - sig)
def tanh(y):
return np.tanh(y)
def tanh_backward(dz, y):
return dz * (1 - np.power(tanh(y), 2))
def relu(y):
return np.maximum(0, y)
def relu_backward(dz, y):
dy = dz.copy()
dy[y < 0] = 0
return dy
2.1.2 loss.py
import numpy as np
def binary_cross_entropy_loss(Y_hat, Y):
"""
二元交叉熵损失函数
:param Y_hat: Y的预测值(样本数,1)
:param Y: Y的真实值(样本数,1)
:return: 交叉熵值
"""
delta = 1e-7
loss = -(np.dot(Y, np.log(Y_hat + delta).T) + np.dot(1 - Y, np.log(1 - Y_hat + delta).T)) / len(Y)
return np.squeeze(loss)
def binary_cross_entropy_loss_backward(Y_hat, Y):
return -(np.divide(Y, Y_hat) - np.divide(1 - Y, 1 - Y_hat))
def cross_entropy_loss(Y_hat, Y):
"""
交叉熵损失函数
:param Y_hat:预测值(样本数,类别数)
:param Y:真实值(样本数,类别数)
:return:交叉熵
"""
m, n = Y_hat.shape
loss = 0
for i in range(m):
loss += -np.dot(Y_hat[i], np.log(Y[i]))
loss /= m
return loss
2.1.3 visualize.py
import os
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class VisualizeTrain():
def __init__(self, model, X, Y):
self.model = model
self.X = X
self.Y = Y
GRID_X_START = -2.5
GRID_X_END = 2.5
GRID_Y_START = -2.5
GRID_Y_END = 2.5
grid = np.mgrid[GRID_X_START:GRID_X_END:500j, GRID_Y_START:GRID_Y_END:500j]
self.grid_2d = grid.reshape(2, -1).T
self.XX, self.YY = grid
plt.ion()
plt.figure(figsize=(16, 12))
plt.subplots_adjust(left=0.20)
plt.subplots_adjust(right=0.80)
self.axes = plt.gca()
self.axes.set(xlabel="$X_1$", ylabel="$X_2$")
def callback_numpy_plot(self, index):
plot_title = "迭代次数{:05}".format(index)
prediction_probs = self.model.forward(np.transpose(self.grid_2d))
prediction_probs = prediction_probs.reshape(prediction_probs.shape[1], 1)
plt.clf()
plt.title(plot_title, fontsize=30)
if (self.XX is not None and self.YY is not None and prediction_probs is not None):
plt.contourf(self.XX, self.YY, prediction_probs.reshape(self.XX.shape), levels=[0, 0.5, 1], alpha=1,
cmap=cm.Spectral)
plt.contour(self.XX, self.YY, prediction_probs.reshape(self.XX.shape), levels=[.5], cmap="Greys", vmin=0,
vmax=.6)
plt.scatter(self.X[0, :], self.X[1, :], c=self.Y.ravel(), s=40, cmap=plt.cm.Spectral, edgecolors='black')
plt.draw()
plt.pause(0.01)
2.1.4 MLP.py
import numpy as np
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from tools.activation import *
from tools.loss import *
from tools.visualize import *
class MLP():
def __init__(self, nn_architecture, seed=99):
self.nn_architecture = nn_architecture
self.learning_rate = 0
self.params_values = {}
self.grad_values = {}
self.memory = {}
self.number_of_layers = len(nn_architecture)
self.visualize_train = None
for layer_id, layer in enumerate(nn_architecture, 1):
layer_input_size = layer['input_dim']
layer_output_size = layer['output_dim']
self.params_values['W' + str(layer_id)] = np.random.randn(layer_input_size, layer_output_size) * 0.1
self.params_values['b' + str(layer_id)] = np.random.randn(layer_output_size, 1) * 0.1
def single_layer_forward_propagation(self, Z_pre, W, b, activation='relu'):
Y = np.dot(W.T, Z_pre) + b
if activation is 'relu':
activation_func = relu
elif activation is 'sigmoid':
activation_func = sigmoid
else:
raise Exception('没有找到该激活函数:' + activation)
return activation_func(Y), Y
def forward(self, X):
Z_curr = X
for layer_id, layer in enumerate(self.nn_architecture, 1):
Z_pre = Z_curr
Z_curr, Y_curr = self.single_layer_forward_propagation(Z_pre, self.params_values['W' + str(layer_id)],
self.params_values['b' + str(layer_id)],
layer['activation'])
self.memory['Y' + str(layer_id)] = Y_curr
self.memory['Z' + str(layer_id)] = Z_curr
return Z_curr
def single_layer_backward_propagation(self, dz_curr, w, b, y, z_pre, activation='relu'):
"""
一层反向传播
:param dz_curr: (样本数,输出层数)
:param w: (输入层数,输出层数)
:param b: (输出层数,1)
:param y: (样本数,输出层数)
:param z_pre: (样本数,输入层数)
:param activation:
:return:
"""
if activation is 'relu':
back_activation_func = relu_backward
elif activation is 'sigmoid':
back_activation_func = sigmoid_backwrad
else:
raise Exception('没有找到该激活函数:' + activation)
m = dz_curr.shape[1] # 样本数
dy = back_activation_func(dz_curr, y)
dw = np.dot(z_pre, dy.T) / m
db = np.sum(dy, axis=1, keepdims=True) / m
dz_pre = np.dot(w, dy)
return dz_pre, dw, db
def backward(self, Y_hat, Y):
"""
反向传播
:param Y_hat:(样本数,1)
:param Y: (样本数,1)
:return:
"""
dz_pre = binary_cross_entropy_loss_backward(Y_hat, Y)
for layer_id, layer in reversed(list(enumerate(self.nn_architecture, 1))):
dz_cur = dz_pre
dz_pre, dw, db = self.single_layer_backward_propagation(dz_cur, self.params_values['W' + str(layer_id)],
self.params_values['b' + str(layer_id)],
self.memory['Y' + str(layer_id)],
self.memory['Z' + str(layer_id - 1)],
layer['activation'])
self.grad_values['dW' + str(layer_id)] = dw
self.grad_values['db' + str(layer_id)] = db
self.update()
def update(self):
for layer_id, layer in enumerate(self.nn_architecture, 1):
self.params_values['W' + str(layer_id)] -= self.learning_rate * self.grad_values['dW' + str(layer_id)]
self.params_values['b' + str(layer_id)] -= self.learning_rate * self.grad_values['db' + str(layer_id)]
def train(self, X, Y, epochs, learning_rate, verbose=False, draw_train=False):
"""
训练
:param X: (样本数,)
:param Y: 二分类标签(样本数,1)
:param epochs: 迭代次数
:param learning_rate: 学习率
:param verbose: 是否显示训练过程
:param callback: 回调函数
:return:
"""
self.learning_rate = learning_rate
self.memory['Z0'] = X
loss_list = []
accuracy_list = []
if (draw_train):
self.visualize_train = VisualizeTrain(self, X, Y)
for i in range(1, epochs + 1):
Y_hat = self.forward(X)
loss = binary_cross_entropy_loss(Y_hat, Y)
accuracy = self.get_accuracy_value(Y_hat, Y)
loss_list.append(loss)
accuracy_list.append(accuracy)
self.backward(Y_hat, Y)
if (i % 100 == 0):
if (verbose):
print('iteration: %d, loss: %f, accuracy: %f' % (i, loss, accuracy))
if (draw_train):
self.visualize_train.callback_numpy_plot(i)
def convert_prob_to_class_binary(self, Y):
Y_ = Y.copy()
Y_[Y_ > 0.5] = 1
Y_[Y_ <= 0.5] = 0
return Y_
def get_accuracy_value(self, Y_hat, Y):
"""
计算准确率
:param Y_hat:预测值(样本数,类别数)
:param Y:真实值(样本数,类别数)
:return:准确率
"""
Y_hat_ = self.convert_prob_to_class_binary(Y_hat)
return (Y_hat_ == Y).all(axis=0).mean()
if __name__ == '__main__':
nn_architecture = [{"input_dim": 2, "output_dim": 25, "activation": "relu"},
{"input_dim": 25, "output_dim": 50, "activation": "relu"},
{"input_dim": 50, "output_dim": 50, "activation": "relu"},
{"input_dim": 50, "output_dim": 25, "activation": "relu"},
{"input_dim": 25, "output_dim": 1, "activation": "sigmoid"}]
mlp = MLP(nn_architecture)
X, Y = make_moons(n_samples=1000, noise=0.2, random_state=100)
Y = Y.reshape(Y.shape[0], 1)
# make_plot(X, Y, "数据集")
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
mlp.train(X_train.T, Y_train.T, 3000, 0.1, verbose=True, draw_train=True)
参考资料
[1] Numpy实现神经网络
[2] matplotlib.pyplot.contourf
[3] matplotlib.pyplot.contour
[4] np.mgrid