Logist Regression代码详解以及Demo
今天大管和大家来聊一聊逻辑回归在sklearn中的具体使用,以及详细的解析。在文章末尾,我们使用官网提供的案例来使用逻辑回归对鸢尾花数据集进行分类。
目录
Logist Regression
#调用函数
#参数Parameters
#属性Attributes
#代码举例
#方法Methods
#实例
Logist Regression
逻辑回归,尽管它的名字,是一个线性模型的分类,而不是回归。Logistic回归在文献中也称为logit回归、最大熵分类(MaxEnt)或对数线性分类器。在这个模型中,描述单个试验可能结果的概率使用逻辑函数来建模。
#调用函数
class sklearn.linear_model.LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='warn', max_iter=100, multi_class='warn', verbose=0, warm_start=False, n_jobs=None)
在多类情况下,如果将“multi_class”选项设置为“OvR”,则训练算法使用one-vs-rest (OvR)模式;如果将“multi_class”选项设置为“ovr”,则使用交叉熵损失。
#参数Parameters
##penalty: str, ‘l1’ or ‘l2’, default: ‘l2’ 用于指定正则项使用L1还是L2,默认使用L2。
##dual: bool, default: False 双重或原始方程。对偶公式仅适用于l2正则。当样本数量大于特征数量时,最好使用dual=False。
##tol: float, default: 1e-4 停止条件设置,默认为1e-4。
##C: float, default: 1.0 正则化强度,较小的值表示更强的正则化。
##fit_intercept:bool, default: True 指定是逻辑回归函数是够需要截距。
##intercept_scaling: float, default 1 只有当解算器“liblinear”被使用并自定义时才有用。fit_intercept设置为True。在这种情况下,x变成[x, self.intercept_scaling], 也就是说,在实例向量的后面加上一个值等于intercept_scaling的“合成”特性。截距变成了intercept_scaling * synthetic_feature_weight。
##class_weight: dict or ‘balanced’, default: None 字典的额形式{class_label: weight}给出类相关联的权重。如果没有给出,所有的类都应该有权重1。
##random_state: int, RandomState instance or None, optional, default: None 数据变换时使用的伪随机数生成器的种子。如果int, random_state是随机数生成器使用的种子; 如果RandomState实例,random_state是随机数生成器;如果没有,随机数生成器就是np.random使用的RandomState实例。当solver == ' sag '或' liblinear '时使用。
##solver: str, {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}, default: ‘liblinear’. 用于优化问题的算法。对于小的数据集,“liblinear”是一个不错的选择,而对于大的数据集,“sag”和“saga”更快。对于多类问题,只有“newton-cg”、“sag”、“saga”和“lbfgs”处理多项损失; “liblinear”仅限于一个对one-versus-rest的方案。“newton-cg”、“lbfgs”和“sag”只处理L2处罚,而“liblinear”和“saga”处理L1处罚。
##max_iter: int, default: 100 仅适用于newton-cg, sag和lbfgs的求解。求解器收敛所需的最大迭代次数。
##multi_class: str, {‘ovr’, ‘multinomial’, ‘auto’}, default: ‘ovr’ 如果选择的选项是' ovr ',那么每个标签都适合一个二进制问题。对于多项式,即使数据是二进制的,损失最小化是多项式损失符合整个概率分布,当解算器= ' liblinear '时,'多项'不可用。“auto”选择“ovr”,如果数据是二进制的,或者如果solver=“liblinear”,否则选择“multinomial”。
##verbose: int, default: 0 对于liblinear和lbfgs求解器,将冗余设置为任意正数。
##warm_start: bool, default: False 当设置为True时,重用前一个调用的解决方案以适应初始化,否则,清除前一个解决方案。
##n_jobs: int or None, optional (default=None) 如果multi_class= ' ovr ' ",则在类之间并行化时使用的CPU核数"。当求解器被设置为“liblinear”时,不管是否指定了“multi_class”,这个参数都会被忽略。
#属性Attributes
##classes_: array, shape (n_classes, ) 已知的分类器标签列表
##coef_: array, shape (1, n_features) or (n_classes, n_features) 特征的系数
##intercept_: array, shape (1,) or (n_classes,) 分类器的独立项(偏置)
##n_iter_: array, shape (n_classes,) or (1, ) 所有类的实际迭代次数。如果是二进制或多项式,它只返回一个元素。对于线性解算器,只给出了所有类的最大迭代次数。
#代码举例
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import LogisticRegression
>>> X, y = load_iris(return_X_y=True)
>>> clf = LogisticRegression(random_state=0, solver='lbfgs',multi_class='multinomial').fit(X, y)
>>> clf.predict(X[:2, :])
array([0, 0])
>>> clf.predict_proba(X[:2, :])
array([[9.8...e-01, 1.8...e-02, 1.4...e-08],
[9.7...e-01, 2.8...e-02, ...e-08]])
>>> clf.score(X, y)
0.97...
#方法Methods
## decision_function(X) 预测样本的置信得分
参数Parameters
X: array_like or sparse matrix, shape (n_samples, n_features) 输入样本
返回值Return
每个(样本,类别)的信心得分。在二元情况下,为自身置信度得分,大于0表示该类被预测
##densify() 转换系数矩阵为密集array的格式。
##fit(X, y, sample_weight=None) 根据训练数据来拟合模型
参数Parameters
X: {array-like, sparse matrix}, shape (n_samples, n_features) 训练数据,其中n_samples为样本个数,n_features为特征个数。
y: array-like, shape (n_samples,) 对于训练数据的标签
sample_weight: array-like, shape (n_samples,) optional 分配给单个样本的权重数组。如果没有提供,那么每个样本的权重都为1。
##get_params(deep=True) 从模型中获取参数
参数Parameters
deep: boolean, optional 如果为真,将返回此估计器的参数以及包含的作为估计器的子对象。
返回值Return
params: mapping of string to any 返回模型参数名所映射的值
##predict(X) 线性模型的预测值
参数Parameters
X: array_like or sparse matrix, shape (n_samples, n_features) 要预测的样本
返回值Return
C: array, shape (n_samples,) 返回预测的值
##score(X, y, sample_weight=None) 返回给定测试数据和标签的平均准确度
参数Parameters
X: array_like or sparse matrix, shape (n_samples, n_features) 要预测的样本
y: array-like, shape = (n_samples) or (n_samples, n_outputs) X的真实标签值
sample_weight: array-like, shape = [n_samples], optional 样本的权重默认不设置
返回值Return
使用测试用本的平均准确度
##set_params(**params) 给模型设置参数。
##predict_log_proba(X) 概率估计的对数
参数Parameters
X: array-like, shape = [n_samples, n_features] 要预测的样本
返回值Return
T: array-like, shape = [n_samples, n_classes] 返回模型中每个类的样本的对数概率(按照类别中的顺序排列)。
##predict_proba(X) 概率估计, 对于多类问题,如果将多类设置为“多项”,则使用softmax函数来查找每个类的预测概率。否则使用one-vs-rest方法。
例如使用logistic函数计算每个类假设为正的概率。并在所有类中规范化这些值。
参数Parameters
X: array-like, shape = [n_samples, n_features] 要预测的样本
返回值Return
T: array-like, shape = [n_samples, n_classes] 返回模型中每个类的样本概率(按照类别中的顺序排列)。
#实例
使用Logistics回归对鸢尾花数据进行三分类。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
### import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features.
Y = iris.target
logreg = LogisticRegression(C=1e5, solver='lbfgs', multi_class='multinomial')
### Create an instance of Logistic Regression Classifier and fit the data.
logreg.fit(X, Y)
### Plot the decision boundary. For that, we will assign a color to each
### point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = .02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
### Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
### Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
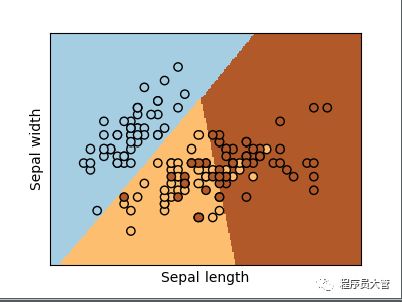
plt.show()下面显示的是鸢尾花数据集的前两个维度(萼片长度和宽度)上的逻辑回归分类器决策边界。数据点根据其标签着色。
多内容下载机器学习资料请扫描下方二维码关注小编公众号:程序员大管
![]()