【02】机器学习基础知识总结

常见的机器学习算法

回归算法	聚类算法	正则化方法

决策树学习	贝叶斯方法	基于核的算法

聚类算法	关联规则学习	人工神经网络

深度学习	降低维度算法	集成算法

​

机器学习分类

根据数据类型的不同，对一个问题的建模有不同的方式。依据不同的学习方式和输入数据，机器学习主要分为以下四种学习方式。

1 监督学习（有数据，有标签），数据映射标签

• 特点：监督学习是使用已知正确答案的示例来训练网络。
  • 已知数据和其一一对应的标签，训练一个预测模型，将输入数据映射到标签的过程。
• 常见应用场景：监督式学习的常见应用场景如分类问题和回归问题。

算法举例
向量机(Support Vector Machine, SVM)
朴素贝叶斯(Naive Bayes)
逻辑回归(Logistic Regression)
K近邻(K-Nearest Neighborhood, KNN)
决策树(Decision Tree)
随机森林(Random Forest)
AdaBoost
线性判别分析(Linear Discriminant Analysis, LDA)
深度学习(Deep Learning)

2 非监督式学习（有数据，无标签）

• 定义：在非监督式学习中，数据并不被特别标识，适用于你具有数据集但无标签的情况。
  • 学习模型是为了推断出数据的一些内在结构。
• 常见应用场景：常见的应用场景包括关联规则的学习以及聚类等。

算法举例
Apriori算法
k-Means算法

3 半监督式学习（数据，部分标签）

• 特点：在此学习方式下，输入数据部分被标记，部分没有被标记，这种学习模型可以用来进行预测。

• 常见应用场景：应用场景包括分类和回归，算法包括一些对常用监督式学习算法的延伸，通过对已标记数据建模，在此基础上，对未标记数据进行预测。

​ 算法举例：常见算法如图论推理算法（Graph Inference）或者拉普拉斯支持向量机（Laplacian SVM）等。

算法举例
图论推理算法（Graph Inference）
拉普拉斯支持向量机（Laplacian SVM）

4 弱监督学习（数据，多个标记）

• 特点：弱监督学习可以看做是有多个标记的数据集合，次集合可以是空集，单个元素，或包含多种情况（没有标记，有一个标记，和有多个标记）的多个元素。

  • 数据集的标签是不可靠的，这里的不可靠可以是标记不正确，多种标记，标记不充分，局部标记等。
  • 已知数据和其一一对应的弱标签，训练一个智能算法，将输入数据映射到一组更强的标签的过程。标签的强弱指的是标签蕴含的信息量的多少，比如相对于分割的标签来说，分类的标签就是弱标签。

• 算法举例：举例，给出一张包含气球的图片，需要得出气球在图片中的位置及气球和背景的分割线，这就是已知弱标签学习强标签的问题。

在企业数据应用的场景下， 人们最常用的可能就是监督式学习和非监督式学习的模型。 在图像识别等领域，由于存在大量的非标识的数据和少量的可标识数据， 目前半监督式学习是一个很热的话题。

监督学习方法（生成VS判别）

$$从概率分布的角度考虑，对于一堆样本数据，每个均有特征X_i对应分类标记y_i。$$

监督学习方法又分生成方法（Generative approach）和判别方法（Discriminative approach），所学到的模型分别称为生成模型（Generative Model）和判别模型（Discriminative Model）

$$生成模型：学习得到联合概率分布P(x,y)，即特征x和标记y共同出现的概率，然后求条件概率分布。能够学习到数据生成的机制。$$

• 由数据学习联合概率密度分布P(X,Y)，然后求出条件概率分布P(Y|X)作为预测的模型，即生成模型：P(Y|X)= P(X,Y)/ P(X)。
• 基本思想是首先建立样本的联合概率概率密度模型P(X,Y)，然后再得到后验概率P(Y|X)，再利用它进行分类

$$判别模型：学习得到条件概率分布P(y|x)，即在特征x出现的情况下标记y出现的概率。$$

• 由数据直接学习决策函数Y=f(X)或者条件概率分布P(Y|X)作为预测的模型，即判别模型。
• 基本思想是有限样本条件下建立判别函数，不考虑样本的产生模型，直接研究预测模型。
• 典型的判别模型包括k近邻，感知级，决策树，支持向量机等。

模型种类	示例	优点	缺点
生成模型	朴素贝叶斯 隐马尔科夫模型 高斯判别分析(GDA) LDA	1）生成给出的是**联合分布，不仅能够由联合分布计算条件分布（反之则不行），还可以给出其他信息，比如可以使用P(x)=求和(P(x|ci)) 来计算边缘分布P(x)。如果一个输入样本的边缘分布P(x)很小的话，那么可以认为学习出的这个模型可能不太适合对这个样本进行分类，分类效果可能会不好，这也是所谓的outlier detection。生成方法可以算出联合概率分布分布P(X,Y)，而判别方法不能。 2）生成模型收敛速度比较快，即当样本数量较多时，生成模型能更快地收敛于真实模型。 3）生成模型能够应付存在隐变量的情况，比如混合高斯模型**就是含有隐变量的生成方法。此时判别方法就不能用。	1）天下没有免费午餐，联合分布是能提供更多的信息，但也需要更多的样本和更多计算，尤其是为了更准确估计类别条件分布，需要增加样本的数目，而且类别条件概率的许多信息是我们做分类用不到，因而如果我们只需要做分类任务，就浪费了计算资源。 2）另外，实践中多数情况下判别模型效果更好。
判别模型	k近邻 感知机 决策树 支持向量机 逻辑回归	1）由于直接学习P(Y，X)或f(X)，可以对数据进行各种程度上的抽象、定义特征并使用特征，因此可以简化学习问题。与生成模型缺点对应，首先是节省计算资源，另外，需要的样本数量也少于生成模型。 2）直接面对预测，准确率往往较生成模型高。 3）判别方法直接学习的是决策函数Y=f(X)或者条件概率分布P(Y，X)，不能反映训练数据本身的特性。但它寻找不同类别之间的最优分类面，反映的是异类数据之间的差异。所以允许我们对输入进行抽象（比如降维、构造等），从而能够简化学习问题。	1）没有生成模型的上述优点。

由生成模型可以得到判别模型，但由判别模型得不到生成模型。

机器学习步骤

步骤
步骤1	数据集的创建和分类
步骤2	数据增强（Data Augmentation）
步骤3	特征工程
步骤4	构建预测模型和损失
步骤5	训练
步骤6	验证和模型选择
步骤7	测试与应用

常用分类算法

1.常用分类算法的优缺点

算法	优点	缺点
Bayes 贝叶斯分类法	1）所需估计的参数少，对于缺失数据不敏感。 2）有着坚实的数学基础，以及稳定的分类效率。	1）需要假设属性之间相互独立，这往往并不成立。（喜欢吃番茄、鸡蛋，却不喜欢吃番茄炒蛋）。 2）需要知道先验概率。 3）分类决策存在错误率。
Decision Tree决策树	1）不需要任何领域知识或参数假设。 2）适合高维数据。 3）简单易于理解。 4）短时间内处理大量数据，得到可行且效果较好的结果。 5）能够同时处理数据型和常规性属性。	1）对于各类别样本数量不一致数据，信息增益偏向于那些具有更多数值的特征。 2）易于过拟合。 3）忽略属性之间的相关性。 4）不支持在线学习。
SVM支持向量机	1）可以解决小样本下机器学习的问题。 2）提高泛化性能。 3）可以解决高维、非线性问题。超高维文本分类仍受欢迎。 4）避免神经网络结构选择和局部极小的问题。	1）对缺失数据敏感。 2）内存消耗大，难以解释。 3）运行和调参略烦人。
KNN K近邻	1）思想简单，理论成熟，既可以用来做分类也可以用来做回归； 2）可用于非线性分类； 3）训练时间复杂度为O(n)； 4）准确度高，对数据没有假设，对outlier不敏感；	1）计算量太大。 2）对于样本分类不均衡的问题，会产生误判。 3）需要大量的内存。 4）输出的可解释性不强。
Logistic Regression逻辑回归	1）速度快。 2）简单易于理解，直接看到各个特征的权重。 3）能容易地更新模型吸收新的数据。 4）如果想要一个概率框架，动态调整分类阀值。	特征处理复杂。需要归一化和较多的特征工程。
Neural Network 神经网络	1）分类准确率高。 2）并行处理能力强。 3）分布式存储和学习能力强。 4）鲁棒性较强，不易受噪声影响。	1）需要大量参数（网络拓扑、阀值、阈值）。 2）结果难以解释。 3）训练时间过长。
Adaboosting	1）adaboost是一种有很高精度的分类器。 2）可以使用各种方法构建子分类器，Adaboost算法提供的是框架。 3）当使用简单分类器时，计算出的结果是可以理解的。而且弱分类器构造极其简单。 4）简单，不用做特征筛选。 5）不用担心overfitting。	对outlier比较敏感

机器学习评估指标

1.常用术语

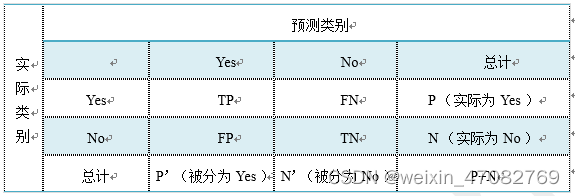
这里首先介绍几个常见的模型评价术语，现在假设我们的分类目标只有两类，计为正例（positive）和负例（negative）分别是：

1. True positives(TP): 被正确地划分为正例的个数，即实际为正例且被分类器划分为正例的实例数；
2. False positives(FP): 被错误地划分为正例的个数，即实际为负例但被分类器划分为正例的实例数；
3. False negatives(FN):被错误地划分为负例的个数，即实际为正例但被分类器划分为负例的实例数；
4. True negatives(TN): 被正确地划分为负例的个数，即实际为负例且被分类器划分为负例的实例数。

​ 表
四个术语的混淆矩阵

评价指标	解释
正确率（accuracy）	正确率是我们最常见的评价指标，accuracy = (TP+TN)/(P+N)，正确率是被分对的样本数在所有样本数中的占比，通常来说，正确率越高，分类器越好。
错误率（error rate）	错误率则与正确率相反，描述被分类器错分的比例，error rate = (FP+FN)/(P+N)，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate。
灵敏度（sensitive）	sensitivity = TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力。
特异性（specificity）	specificity = TN/N，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力。
精度（precision）	precision=TP/(TP+FP)，精度是精确性的度量，表示被分为正例的示例中实际为正例的比例。
召回率	召回率是覆盖面的度量，度量有多个正例被分为正例，recall=TP/(TP+FN)=TP/P=sensitivity，可以看到召回率与灵敏度是一样的。
其他评价指标	计算速度：分类器训练和预测需要的时间； 鲁棒性：处理缺失值和异常值的能力； 可扩展性：处理大数据集的能力； 可解释性：分类器的预测标准的可理解性，像决策树产生的规则就是很容易理解的，而神经网络的一堆参数就不好理解，我们只好把它看成一个黑盒子。
F1-Score	精度和召回率反映了分类器分类性能的两个方面。如果综合考虑查准率与查全率，可以得到新的评价指标F1-score，也称为综合分类率：$F1=\frac{2\times precision\times recall}{precision+recall}$。
P-R曲线	查准率为纵轴，查全率为横轴，作图
Confusion Matrix	混淆矩阵
ROC	ROC曲线
AUC	ROC下的面积

2.分类模型常用评估方法

指标	描述
Accuracy	准确率
Precision	精准度/查准率
Recall	召回率/查全率
P-R曲线	查准率为纵轴，查全率为横轴，作图
F1	F1值
Confusion Matrix	混淆矩阵
ROC	ROC曲线
AUC	ROC曲线下的面积

3.回归模型常用评估方法

指标	描述
Mean Square Error (MSE, RMSE)	平均方差
Absolute Error (MAE, RAE)	绝对误差
R-Squared	R平方值

可视化的指标

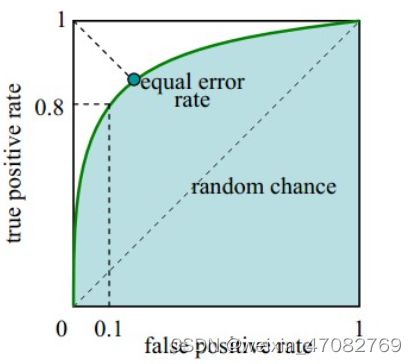
• ROC曲线是（Receiver Operating Characteristic Curve，受试者工作特征曲线）的简称
  • 是以灵敏度（真阳性率）为纵坐标，以1减去特异性（假阳性率）为横坐标绘制的性能评价曲线。
  • 可以将不同模型对同一数据集的ROC曲线绘制在同一笛卡尔坐标系中，ROC曲线越靠近左上角，说明其对应模型越可靠。
  • 也可以通过ROC曲线下面的面积（Area Under Curve, AUC）来评价模型，AUC越大，模型越可靠。

机器学习中常见的损失函数

对比Loss Function，Cost Function，Object Function

函数	含义
损失函数（Loss Function ）	是定义在单个样本上的，算的是一个样本的误差。
代价函数（Cost Function ）	定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。
目标函数（Object Function）	最终需要优化的函数。等于经验风险+结构风险（也就是代价函数 + 正则化项）。代价函数最小化，降低经验风险，正则化项最小化降低

1.常用损失函数

• 损失函数（Loss Function）又叫做误差函数，用来衡量算法的运行情况，估量模型的预测值与真实值的不一致程度，是一个非负实值函数，通常使用$
  L(Y, f(x))$来表示。损失函数越小，模型的鲁棒性就越好。
• 损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。

机器学习通过对算法中的目标函数进行不断求解优化，得到最终想要的结果。分类和回归问题中，通常使用损失函数或代价函数作为目标函数。
损失函数用来评价预测值和真实值不一样的程度。通常损失函数越好，模型的性能也越好。
损失函数可分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是在经验风险损失函数上加上正则项。下面介绍常用的损失函数：

（1）.0-1损失函数

如果预测值和目标值相等，值为0，如果不相等，值为1。
$$L(Y,f(x))=\{\begin{array}{ll}1,& Y\ne f(x)\\ 0,& Y=f(x)\end{array}$$

一般的在实际使用中，相等的条件过于严格，可适当放宽条件：

$$L(Y,f(x))=\{\begin{array}{ll}1,& |Y-f(x)|⩾T\\ 0,& |Y-f(x)|<T\end{array}$$

（2）绝对值损失函数

和0-1损失函数相似，绝对值损失函数表示为：
$$L(Y,f(x))=|Y-f(x)|$$

（3）平方损失函数（最小二乘）

$$L(Y,f(x))=\sum _N{(Y-f(x))}^2$$

• 这点可从最小二乘法和欧几里得距离角度理解。最小二乘法的原理是，最优拟合曲线应该使所有点到回归直线的距离和最小。

（4）对数损失函数（逻辑回归）

$$L(Y,P(Y|X))=-\log P(Y|X)$$

• 常见的逻辑回归使用的就是对数损失函数，有很多人认为逻辑回归的损失函数是平方损失，其实不然。
• 逻辑回归它假设样本服从伯努利分布（0-1分布），进而求得满足该分布的似然函数，接着取对数求极值等。
• 逻辑回归推导出的经验风险函数是最小化负的似然函数，从损失函数的角度看，就是对数损失函数。

（5）指数损失函数（Adaboost）

指数损失函数的标准形式为：
$$L(Y,f(x))=\exp (-Yf(x))$$

例如AdaBoost就是以指数损失函数为损失函数。

（6）Hinge损失函数（支持向量机）

Hinge损失函数的标准形式如下：
$$L(y)=\max (0,1-ty)$$

统一的形式：
$$L(Y,f(x))=\max (0,Yf(x))$$

其中y是预测值，范围为(-1,1)，t为目标值，其为-1或1。

在线性支持向量机中，最优化问题可等价于

$$\underset{\min }{w,b}\sum _{i=1}^N(1-y_i(w{x}_i+b))+\lambda \Vert w{\Vert }^2$$

上式相似于下式

$$\frac{1}{m}\sum _{i=1}^{N}l(w{x}_i+b{y}_i)+\Vert w{\Vert }^2$$

其中$l(w{x}_i+b{y}_i)$是Hinge损失函数，$\Vert w{\Vert }^2$可看做为正则化项。

2.常用的代价函数

（1）二次代价函数（quadratic cost）：适合神经元为线性：

$$J=\frac{1}{2n}\sum _x\Vert y(x)-a^L(x){\Vert }^2$$

其中，$J$表示代价函数，$x$表示样本，$y$表示实际值，$a$表示输出值，$n$表示样本的总数。

使用一个样本为例简单说明，此时二次代价函数为：
$$J=\frac{(y-a{)}^2}{2}$$
假如使用梯度下降法（Gradient descent）来调整权值参数的大小，权值$w$和偏置$b$的梯度推导如下：
$$\frac{\partial J}{\partial b}=(a-y){\sigma }^{\prime }(z)$$
其中，$z$表示神经元的输入，$\sigma$表示激活函数。权值$w$和偏置$b$的梯度跟激活函数的梯度成正比，激活函数的梯度越大，权值$w$和偏置$b$的大小调整得越快，训练收敛得就越快。

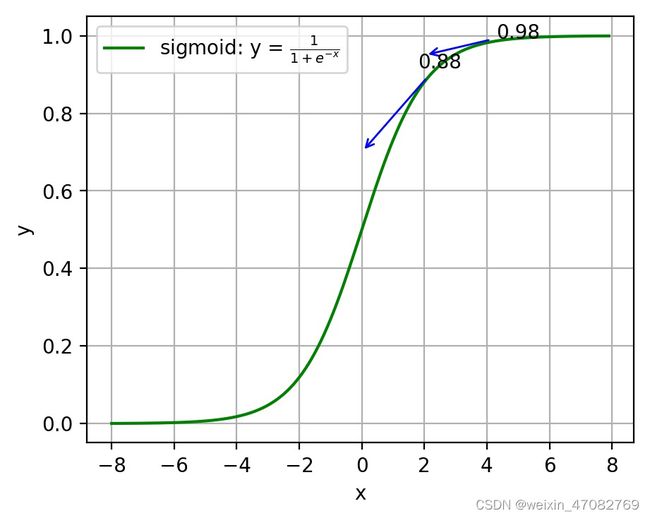
注：神经网络常用的激活函数为sigmoid函数，该函数的曲线如下图2-6所示：

​ 图 sigmoid函数曲线

如上图所示，对0.88和0.98两个点进行比较：
​ 假设目标是收敛到1.0。0.88离目标1.0比较远，梯度比较大，权值调整比较大。0.98离目标1.0比较近，梯度比较小，权值调整比较小。调整方案合理。
​ 假如目标是收敛到0。0.88离目标0比较近，梯度比较大，权值调整比较大。0.98离目标0比较远，梯度比较小，权值调整比较小。调整方案不合理。
​ 原因：在使用sigmoid函数的情况下, 初始的代价（误差）越大，导致训练越慢。

（2）交叉熵代价函数（cross-entropy）：适合神经元为S型函数：

$$J=-\frac{1}{n}\sum _x[y\ln a+(1-y)\ln (1-a)]$$

其中，$J$表示代价函数，$x$表示样本，$y$表示实际值，$a$表示输出值，$n$表示样本的总数。
权值$w$和偏置$b$的梯度推导如下：
$$\frac{\partial J}{\partial w_j}=\frac{1}{n}\sum _x{x}_j(\sigma (z)-y)，\frac{\partial J}{\partial b}=\frac{1}{n}\sum _x(\sigma (z)-y)$$

当误差越大时，梯度就越大，权值$w$和偏置$b$调整就越快，训练的速度也就越快。
二次代价函数适合输出神经元是线性的情况，交叉熵代价函数适合输出神经元是S型函数的情况。

（3）对数似然代价函数（log-likelihood cost）：适合Softmax函数：

• 对数似然函数常用来作为softmax回归的代价函数。深度学习中普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数似然代价函数。
• 对数似然代价函数与softmax的组合和交叉熵与sigmoid函数的组合非常相似。对数似然代价函数在二分类时可以化简为交叉熵代价函数的形式。
• 在tensorflow中：
  • 与sigmoid搭配使用的交叉熵函数：tf.nn.sigmoid_cross_entropy_with_logits()。
  • 与softmax搭配使用的交叉熵函数：tf.nn.softmax_cross_entropy_with_logits()。
• 在pytorch中：
  • 与sigmoid搭配使用的交叉熵函数：torch.nn.BCEWithLogitsLoss()。
  • 与softmax搭配使用的交叉熵函数：torch.nn.CrossEntropyLoss()。

机器学习的优化方法

1.对梯度下降法调优

实际使用梯度下降法时，各项参数指标不能一步就达到理想状态，对梯度下降法调优主要体现在以下几个方面：

（1）算法迭代步长$\alpha$选择。
在算法参数初始化时，有时根据经验将步长初始化为1。实际取值取决于数据样本。可以从大到小，多取一些值，分别运行算法看迭代效果，如果损失函数在变小，则取值有效。如果取值无效，说明要增大步长。但步长太大，有时会导致迭代速度过快，错过最优解。步长太小，迭代速度慢，算法运行时间长。

（2）参数的初始值选择。
初始值不同，获得的最小值也有可能不同，梯度下降有可能得到的是局部最小值。如果损失函数是凸函数，则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。

（3）标准化处理。
由于样本不同，特征取值范围也不同，导致迭代速度慢。为了减少特征取值的影响，可对特征数据标准化，使新期望为0，新方差为1，可节省算法运行时间。

2.常用的梯度下降方法对比

假设函数为：
$$h_{\theta }(x_0,x_1,...,x_3)={\theta }_0{x}_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n$$
损失函数为：
$$J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{2m}\sum _{j=0}^m(h_{\theta }(x_0^j,x_1^j,...,x_n^j)-y^j{)}^2$$
其中，$m$为样本个数，$j$为参数个数。

方法	求解思路	特点
批量梯度下降	a) 得到每个$ \theta $对应的梯度：$$\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{m}{\sum }_{j=0}^m(h_{\theta }(x_0^j<br/>,x_1^j,...,x_n^j)-y^j)x_i^j$$ b) 由于是求最小化风险函数，所以按每个参数 $ \theta $ 的梯度负方向更新 $ \theta_i $ ：$${\theta }_i={\theta }_i-\frac{1}{m}\sum _{j=0}^m(h_{\theta }(x_0^j<br/>,x_1^j,...,x_n^j)-y^j)x_i^j$$ c) 从上式可以注意到，它得到的虽然是一个全局最优解，但每迭代一步，都要用到训练集所有的数据，如果样本数据很大，这种方法迭代速度就很慢。	a）采用所有数据来梯度下降。 b）批量梯度下降法在样本量很大的时候，训练速度慢。
随机梯度下降	a) 相比批量梯度下降对应所有的训练样本，随机梯度下降法中损失函数对应的是训练集中每个样本的粒度：$$\begin{gathered} J({\theta }_0,{\theta }_1,...,{\theta }_n)= \\ \frac{1}{m}\sum _{j=0}^m(y^j-h_{\theta }(x_0^j,x_1^j,...,x_n^j){)}^2= \\ \frac{1}{m}\sum _{j=0}^{m}cost(\theta ,(x^j,y^j)) \end{gathered}$$ b）对每个参数 θ 按梯度方向更新 :$${\theta }_i={\theta }_i+(y^j-h_{\theta }(x_0^j,x_1^j,...,x_n^j))$$ c) 随机梯度下降是通过每个样本来迭代更新一次。 随机梯度下降伴随的一个问题是噪音较批量梯度下降要多，使得随机梯度下降并不是每次迭代都向着整体最优化方向。	a）随机梯度下降用一个样本来梯度下降。 b）训练速度很快。 c）随机梯度下降法仅仅用一个样本决定梯度方向，导致解有可能不是全局最优。 d）收敛速度来说，随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不
小批量梯度下降	对于总数为$m$个样本的数据，根据样本的数据，选取其中的$n(1<n<m)$个子样本来迭代。其参数$\theta$按梯度方向更新${\theta }_i$公式如下： $${\theta }_i={\theta }_i-\alpha \sum _{j=t}^{t+n-1}(h_{\theta }(x_0^j,x_1^j,...,x_n^j)-y^j)x_i^j$$

2.性能比较

随机梯度下降（SGD）、批量梯度下降（BGD）、小批量梯度下降（Mini-batch GD）、和Online GD的区别：

	BGD	SGD	Mini-batch GD	Online GD
训练集	固定	固定	固定	实时更新
单次迭代样本数	整个训练集	单个样本	训练集的子集	根据具体算法定
算法复杂度	高	低	一般	低
时效性	低	一般	一般	高
收敛性	稳定	不稳定	较稳定	不稳定

机器学习的偏差、误差、方差

• 经验误差（empirical error）：也叫训练误差（training error），模型在训练集上的误差。
• 泛化误差（generalization error）：模型在新样本集（测试集）上的误差称为“泛化误差”。

在机器学习中，Bias(偏差)，Error(误差)，和Variance(方差)存在以下区别和联系：

对于Error：

• 误差（error）：一般地，我们把学习器的**实际预测输出与样本的真是输出之间的差异称为“误差”**。

• Error = Bias + Variance + Noise，Error反映的是整个模型的准确度。

对于Noise:

噪声：描述了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。

对于Bias：

• Bias衡量模型拟合训练数据的能力（训练数据不一定是整个 training dataset，而是只用于训练它的那一部分数据，例如：mini-batch），Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度。
• Bias 越小，拟合能力越高（可能产生overfitting）；反之，拟合能力越低（可能产生underfitting）。
• 偏差越大，越偏离真实数据，如下图第二行所示。

对于Variance：

• 方差公式：$S_N^2=\frac{1}{N}{\sum }_{i=1}^N(x_i-\bar{x}{)}^2$

• Variance描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散，模型的稳定程度越差。

• Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。

• Variance越小，模型的泛化的能力越高；反之，模型的泛化的能力越低。

• 如果模型在训练集上拟合效果比较优秀，但是在测试集上拟合效果比较差劣，则方差较大，说明模型的稳定程度较差，出现这种现象可能是由于模型对训练集过拟合造成的。
  

机器学习的过拟合和欠拟合

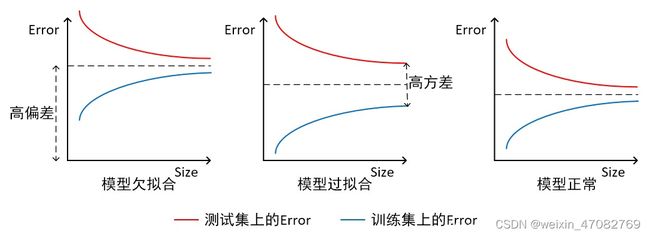
如上图所示，我们可以直观看出欠拟合和过拟合的区别：

模型欠拟合：在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大；

模型过拟合：在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。

模型正常：在训练集以及测试集上，同时具有相对较低的偏差以及方差。

1.解决方法

过拟合	欠拟合
1.添加其他特征项。组合、泛化、相关性、上下文特征、平台特征等特征是特征添加的重要手段，有时候特征项不够会导致模型欠拟合。	1.重新清洗数据，数据不纯会导致过拟合，此类情况需要重新清洗数据
2.添加多项式特征。例如将线性模型添加二次项或三次项使模型泛化能力更强。例如，FM（Factorization Machine）模型、FFM（Field-aware Factorization Machine）模型，其实就是线性模型，增加了二阶多项式，保证了模型一定的拟合程度。	2.增加训练样本数量
3.可以增加模型的复杂程度。	3.降低模型复杂程度
4. 减小正则化系数。正则化的目的是用来防止过拟合的，但是现在模型出现了欠拟合，则需要减少正则化参数。	4.增大正则项系数
	5. 采用dropout方法，dropout方法，通俗的讲就是在训练的时候让神经元以一定的概率不工作。
	6.early stopping
	7.减少迭代次数
	8.增大学习率
	9.添加噪声数据
	10.树结构中，可以对树进行剪枝。
	11. 减少特征项。