Advances in Graph Neural Networks笔记4：Heterogeneous Graph Neural Networks

诸神缄默不语-个人CSDN博文目录

本书网址：https://link.springer.com/book/10.1007/978-3-031-16174-2
本文是本书第四章的学习笔记。
感觉这一章写得不怎么样。以研究生组会讲异质图神经网络主题论文作为标准的话，倒是还行，介绍了HGNN的常见范式和三个经典模型。以教材或综述作为标准的话，建议别买。

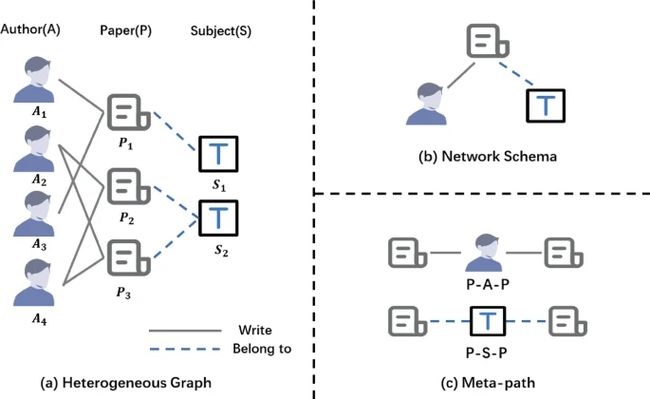
1. HGNN

两步信息聚合：

对目标节点

1. node-level：对每个metapath聚合所有邻居节点
2. semantic level：聚合所有metapath表征

本文介绍的方法关注两个问题：deep degradation phenomenon and discriminative power

2. heterogeneous graph propagation network (hpn)

分析deep degradation phenomenon问题，减缓semantic confusion

2.1 semantic confusion

semantic confusion类似同质图GNN中的过拟合问题

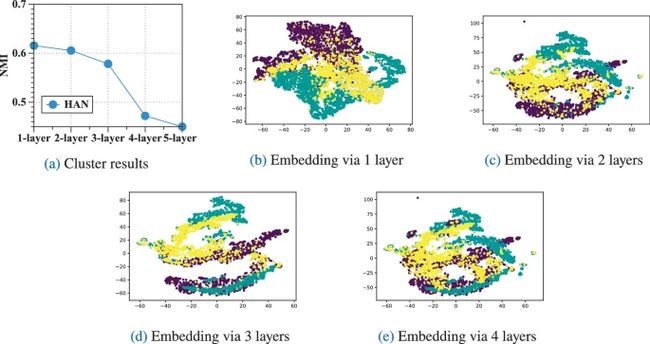
HAN模型在不同层上的聚类结果和论文节点表征的可视化图像，每种颜色代表一种标签（研究领域）。

（本文中对semantic confusion现象的解释很含混，略）

HPN一文证明了HGNN和mutiple meta-paths-based random walk是等价的：
multiple meta-paths-based random walk（感觉跟同质图随机游走也差不太多嘛，就是多个用metapath处理如同质图的随机游走概率叠起来）：

加上步数到极限以后，数学部分我就不太懂了。总之单看表示形式的话依然跟同质图随机游走相似，意思就是说最终分布只与metapaths有关，与初始状态无关：

与之相对，meta-path-based random walk with restart的极限分布是与初始状态有关的：
meta-path-based random walk with restart：${\mathbf{\pi }}^{\Phi ,k}\left(\mathbf{i}\right)=(1-\gamma )\cdot {\text{M}}^{\Phi }\cdot {\mathbf{\pi }}^{\Phi ,k-1}\left(\mathbf{i}\right)+\gamma \cdot \mathbf{i}$

2.2 HPN模型架构

HPN包含两部分：

1. semantic propagation mechanism：除基于meta-path-based neighbors聚合信息外，还以一合适的权重吸收节点的局部语义信息，这样即使层数加深也能学习节点的局部信息（我说这逻辑听起来像APPNP啊）
2. semantic fusion mechanism：学习metapaths的重要性

1. Semantic Propagation Mechanism
   参考meta-path-based random walk with restart：
   对每个metapath邻居，先对节点做线性转换，然后聚合邻居信息（一式是底下两式的加总）：
   $$\begin{array}{rl}& {\text{Z}}^{\Phi }={\mathcal{P}}_{\Phi }(\text{X})=g_{\Phi }(f_{\Phi }(\text{X}))\\ & {\text{H}}^{\Phi }=f_{\Phi }(\text{X})=\sigma (\text{X}\cdot {\text{W}}^{\Phi }+{\text{b}}^{\Phi })\\ & {\text{Z}}^{\Phi ,k}=g_{\Phi }({\text{Z}}^{\Phi ,k-1})=(1-\gamma )\cdot {\text{M}}^{\Phi }\cdot {\text{Z}}^{\Phi ,k-1}+\gamma \cdot {\text{H}}^{\Phi }\end{array}$$
2. Semantic Fusion Mechanism：注意力机制
   $$\begin{array}{rl}& \text{Z}=\mathcal{F}({\text{Z}}^{{\Phi }_1},{\text{Z}}^{{\Phi }_2},\dots ,{\text{Z}}^{{\Phi }_P})\\ & w_{{\Phi }_p}=\frac{1}{|\mathcal{V}|}\sum _{i\in \mathcal{V}}{\text{q}}^{\text{T}}\cdot \tanh (\text{W}\cdot {\text{z}}_i^{{\Phi }_p}+\text{b})\\ & {\beta }_{{\Phi }_p}=\frac{\exp (w_{{\Phi }_p})}{{\sum }_{p=1}^P\exp (w_{{\Phi }_p})}\\ & \text{Z}=\sum _{p=1}^P{\beta }_{{\Phi }_p}\cdot {\text{Z}}^{{\Phi }_p}\end{array}$$

2.3 HPN损失函数

半监督节点分类的损失函数：
$$\mathcal{L}=-\sum _{l\in {\mathcal{Y}}_L}{\text{Y}}_l\cdot \ln ({\text{Z}}_l\cdot \text{C})$$

无监督节点推荐（？这什么任务）的损失函数，BPR loss with negative sampling：
$$\begin{array}{r}\mathcal{L}=-\sum _{(u,v)\in \Omega }\log \sigma \left({\text{z}}_u^{\top }{\text{z}}_v\right)-\sum _{\left(u^{},v^{\prime }\right)\in {\Omega }^{-}}\log \sigma \left(-{\text{z}}_u^{\top }{\text{z}}_{v^{\prime }}\right),\end{array}$$
第一项是observed (positive) node pairs，第二项是negative node pairs sampled from all unobserved node pairs

（HPN实验部分略。简单地说，做了ablation study，做了无监督节点聚类任务，验证了模型对层级加深的鲁棒性（与HAN对比））

2. distance encoding-based heterogeneous graph neural network (DHN)

关注discriminative power：在聚合时加入heterogeneous distance encoding (HDE)（distance encoding (DE) 也是一个同质图GNN中用过的概念）

Heterogeneous Graph Neural Network with Distance Encoding

传统HGNN嵌入各个节点，本文关注节点之间的关联。

2.1 HDE概念定义

heterogeneous shortest path distance：节点数最少路径的节点数

上图中所指的图片就是下图：

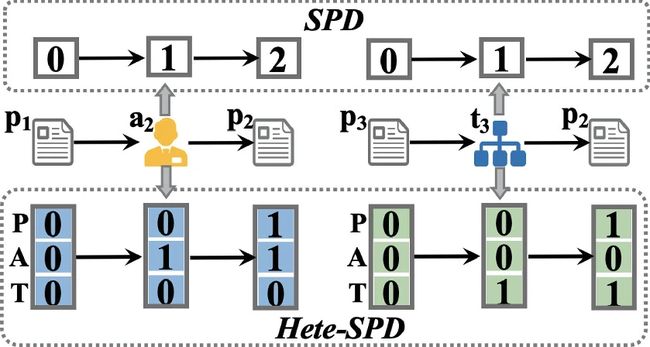
HDE
异质图最短路径距离Hete-SPD：每一维度衡量一类节点在最短路径中出现的次数（不包括第一个节点）

目标节点对锚节点（组）的HDE：目标节点对所有锚节点Hete-SPD先嵌入，后融合

2.2 DHN+链路预测

Heterogeneous Distance Encoding for Link Prediction

目标节点分别是节点对的两个节点，锚节点组也就是这两个节点。

1. Node Embedding Initialization：HDE
2. Heterogeneous distance encoding：仅计算k-hop heterogeneous enclosing subgraph的HDE
3. Heterogeneous type encoding
   $$\begin{array}{rl}& {\text{c}}_i=onehot(\varphi (i))\\ & {\text{e}}_i^{\{u,v\}}=\sigma ({\text{W}}_0\cdot {\text{c}}_i||{\text{h}}_i^{\{u,v\}}+{\text{b}}_0)\end{array}$$
4. Heterogeneous Graph Convolution：先抽样邻居节点
   $$\begin{array}{r}{\text{x}}_{u,l}^{\{u,v\}}=\sigma ({\text{W}}^l\cdot ({\text{x}}_{u,l-1}^{\{u,v\}}||Avg\{{\text{x}}_{i,l-1}^{\{u,v\}}\}+{\text{b}}^l),\forall i\in {\mathcal{N}}_u^{\{u,v\}}\end{array}$$
5. Loss Function and Optimization
   $$\begin{array}{rl}& {\hat{y}}_{u,v}=\sigma \left({\text{W}}_1\cdot ({\text{z}}_u^{\{u,v\}}||{\text{z}}_v^{\{u,v\}})+b_1\right)\\ & \mathcal{L}=\sum _{(u,v)\in {\mathcal{E}}^{+}\cup {\mathcal{E}}^{-}}\left(y_{u,v}\log {\hat{y}}_{u,v}+\left(1-y_{u,v}\right)\log \left(1-{\hat{y}}_{u,v}\right)\right)\end{array}$$

（实验部分略。同时做了transductive和inductive场合下的链路预测任务）

3. self-supervised heterogeneous graph neural network with co-contrastive learning (HeCo)

关注discriminative power：使用cross-view contrastive mechanism同时捕获局部和高阶结构

以前的工作：原网络VS破坏后的网络
HeCo选择的view：network schema（局部结构） and meta-path structure（高阶结构）

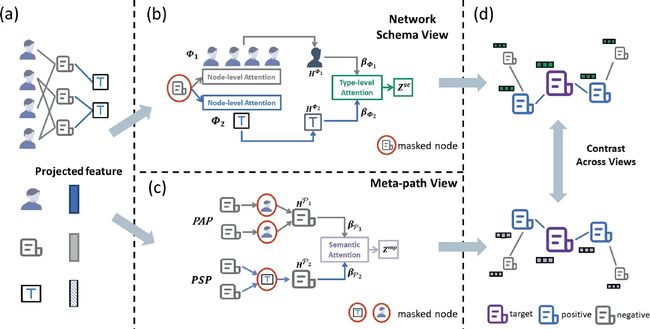
从两个view编码节点（编码时应用view mask mechanism），在两个view-specific embeddings之间应用对比学习。

1. Node Feature Transformation：每种节点都映射到固定维度
   $$\begin{array}{r}{h}_i=\sigma \left(W_{{\varphi }_i}\cdot x_i+b_{{\varphi }_i}\right)\end{array}$$
2. Network Schema View Guided Encoder
   attention：节点级别和类别级别
   
   对某一metapath的邻居（在实践中是抽样一部分节点），应用节点级别attention：
   $$\begin{array}{rl}& h_i^{{\Phi }_m}=\sigma \left(\sum _{j\in N_i^{{\Phi }_m}}{\alpha }_{i,j}^{{\Phi }_m}\cdot h_j\right)\\ & {\alpha }_{i,j}^{{\Phi }_m}=\frac{\exp \left(LeakyReLU\left({\text{a}}_{{\Phi }_m}^{\top }\cdot [h_i||h_j]\right)\right)}{\sum _{l\in N_i^{{\Phi }_m}}\exp \left(LeakyReLU\left({\text{a}}_{{\Phi }_m}^{\top }\cdot [h_i||h_l]\right)\right)}\end{array}$$
   
   对所有metapath的嵌入，应用类别级别attention：
   $$\begin{array}{rl}{w}_{{\Phi }_m}& =\frac{1}{|V|}\sum _{i\in V}{\text{a}}_{sc}^{\top }\cdot \tanh \left({\text{W}}_{sc}{h}_i^{{\Phi }_m}+{\text{b}}_{sc}\right)\\ {\beta }_{{\Phi }_m}& =\frac{\exp \left(w_{{\Phi }_m}\right)}{{\sum }_{i=1}^S\exp \left(w_{{\Phi }_i}\right)}\\ z_i^{sc}& =\sum _{m=1}^S{\beta }_{{\Phi }_m}\cdot h_i^{{\Phi }_m}\end{array}$$

3. Meta-Path View Guided Encoder
   meta-path表示语义相似性，用meta-path specific GCN编码：
   $$\begin{array}{r}{h}_i^{{\mathcal{P}}_n}=\frac{1}{d_i+1}{h}_i+\sum _{j\in N_i^{{\mathcal{P}}_n}}\frac{1}{\sqrt{(d_i+1)(d_j+1)}}{h}_j\end{array}$$
   在所有metapath的表征上加attention：
   $$\begin{array}{rl}{z}_i^{mp}& =\sum _{n=1}^M{\beta }_{{\mathcal{P}}_n}\cdot h_i^{{\mathcal{P}}_n}\\ w_{{\mathcal{P}}_n}& =\frac{1}{|V|}\sum _{i\in V}{\text{a}}_{mp}^{\top }\cdot \tanh \left({\text{W}}_{mp}{h}_i^{{\mathcal{P}}_n}+{\text{b}}_{mp}\right)\\ {\beta }_{{\mathcal{P}}_n}& =\frac{\exp \left(w_{{\mathcal{P}}_n}\right)}{{\sum }_{i=1}^M\exp \left(w_{{\mathcal{P}}_i}\right)}\end{array}$$
4. 增加对比难度：view mask mechanism
   
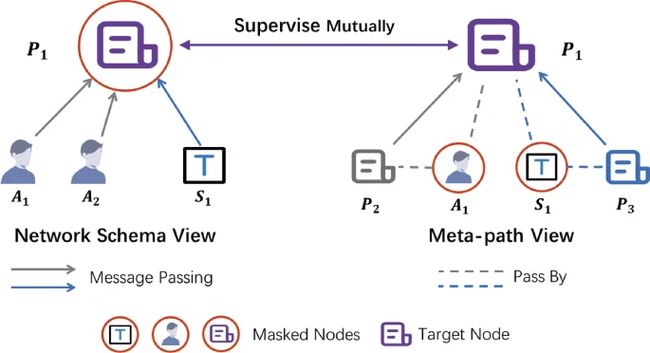
   network schema view：不使用目标节点本身上一级别的嵌入
   meta-path view：不使用与目标节点不同类（不是目标节点基于metapath的邻居的节点）的嵌入
5. Collaboratively Contrastive Optimization
   损失函数：传统对比学习+图数据
   
   将两个view得到的嵌入映射到对比学习的隐空间：
   $$\begin{array}{r}\begin{array}{rl}{z}_i^{sc}\_proj& =W^{(2)}\sigma \left(W^{(1)}{z}_i^{sc}+b^{(1)}\right)+b^{(2)}\\ z_i^{mp}\_proj& =W^{(2)}\sigma \left(W^{(1)}{z}_i^{mp}+b^{(1)}\right)+b^{(2)}\end{array}\end{array}$$
   计算两个节点之间连的metapath数：${\mathbb{C}}_i(j)=\sum _{n=1}^{M}1\left(j\in N_i^{{\mathcal{P}}_n}\right)$（$1(\cdot )$是indicator function）
   将与节点i有metapath相连的节点组成集合$S_i=\{j|j\in Vand{\mathbb{C}}_i(j)\ne 0\}$，基于${\mathbb{C}}_i(\cdot )$数降序排列，如果节点集合元素数大于某一阈值，选出该阈值数个正样本${\mathbb{P}}_i$，没选出来的作为负样本${\mathbb{N}}_i$
   
   计算network schema view的对比损失：
   $$\begin{array}{r}{\mathcal{L}}_i^{sc}=-\log \frac{{\sum }_{j\in {\mathbb{P}}_i}exp\left(sim\left(z_i^{sc}\_proj,z_j^{mp}\_proj\right)/\tau \right)}{{\sum }_{k\in \{{\mathbb{P}}_i\bigcup {\mathbb{N}}_i\}}exp\left(sim\left(z_i^{sc}\_proj,z_k^{mp}\_proj\right)/\tau \right)}\end{array}$$
   
   总的学习目标：
   $$\begin{array}{r}\mathcal{J}=\frac{1}{|V|}\sum _{i\in V}\left[\lambda \cdot {\mathcal{L}}_i^{sc}+\left(1-\lambda \right)\cdot {\mathcal{L}}_i^{mp}\right]\end{array}$$

（和前两篇一样，实验部分略。重要比较baseline有single-view的对比学习方法DMGI。做了节点分类任务，和Collaborative Trend Analysis（计算随训练epoch数增加，attention变化情况。可以发现两个view上attention是协同演变的））

4. Further Reading

惯例啦，因为参考文献序号匹配不上，所以不确定我找的论文 是否正确。
分层级聚合/intent recommendation/文本分类/GTN-软择边类型、自动生成metapaths/HGT-用heterogeneous mutual attention聚合meta-relation triplet/MAGNN-用relational rotation encoder聚合meta-path instances

1. Neural graph collaborative filtering
2. HGNN: Hyperedge-based graph neural network for MOOC Course Recommendation
3. COSNET: Connecting Heterogeneous Social Networks with Local and Global Consistency
4. Metapath-guided Heterogeneous Graph Neural Network for Intent Recommendation
5. IntentGC: a Scalable Graph Convolution Framework Fusing Heterogeneous Information for Recommendation
6. Heterogeneous Graph Attention Networks for Semi-supervised Short Text Classification
7. Graph Transformer Networks
8. Heterogeneous Graph Transformer
9. MAGNN: Metapath Aggregated Graph Neural Network for Heterogeneous Graph Embedding：聚合每个metapath实例内所有节点的信息，然后聚合到每个metapath上，然后将所有metapath表征聚合到目标节点上