神经网络与深度学习作业9:分别使用numpy和pytorch实现BPTT
神经网络与深度学习作业9:分别使用numpy和pytorch实现BPTT
- 6-1P:推导RNN反向传播算法BPTT.
- 6-2P:设计简单RNN模型,分别用Numpy、Pytorch实现反向传播算子,并代入数值测试.
- 总结
- References:
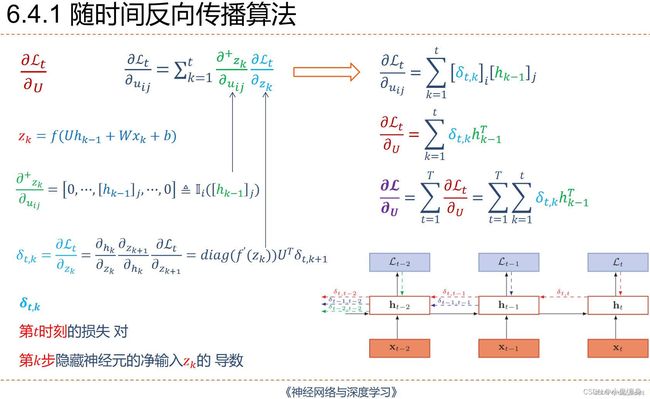
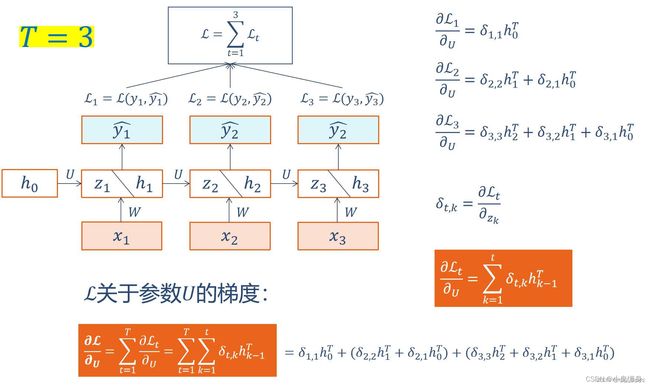
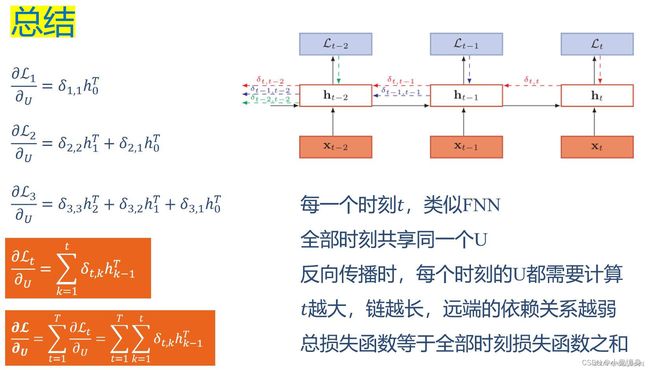
6-1P:推导RNN反向传播算法BPTT.
手动推导实现:
6-2P:设计简单RNN模型,分别用Numpy、Pytorch实现反向传播算子,并代入数值测试.
代码实现:
def rnn_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network described in Figure (3).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of caches, x)
"""
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and Wy
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
### START CODE HERE ###
# initialize "a" and "y" with zeros (≈2 lines)
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# Initialize a_next (≈1 line)
a_next = a0
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈1 line)
a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:, :, t] = a_next
# Save the value of the prediction in y (≈1 line)
y_pred[:, :, t] = yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
def rnn_backward(da, caches):
"""
Implement the backward pass for a RNN over an entire sequence of input data.
Arguments:
da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x)
caches -- tuple containing information from the forward pass (rnn_forward)
Returns:
gradients -- python dictionary containing:
dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x)
da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m)
dWax -- Gradient w.r.t the input's weight matrix, numpy-array of shape (n_a, n_x)
dWaa -- Gradient w.r.t the hidden state's weight matrix, numpy-arrayof shape (n_a, n_a)
dba -- Gradient w.r.t the bias, of shape (n_a, 1)
"""
### START CODE HERE ###
# Retrieve values from the first cache (t=1) of caches (≈2 lines)
(caches, x) = caches
(a1, a0, x1, parameters) = caches[0] # t=1 时的值
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈6 lines)
dx = np.zeros((n_x, m, T_x))
dWax = np.zeros((n_a, n_x))
dWaa = np.zeros((n_a, n_a))
dba = np.zeros((n_a, 1))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
# Loop through all the time steps
for t in reversed(range(T_x)):
# Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
gradients = rnn_cell_backward(da[:, :, t] + da_prevt, caches[t]) # da[:,:,t] + da_prevt ,每一个时间步后更新梯度
# Retrieve derivatives from gradients (≈ 1 line)
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients[
"dWaa"], gradients["dba"]
# Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
# Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line)
da0 = da_prevt
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
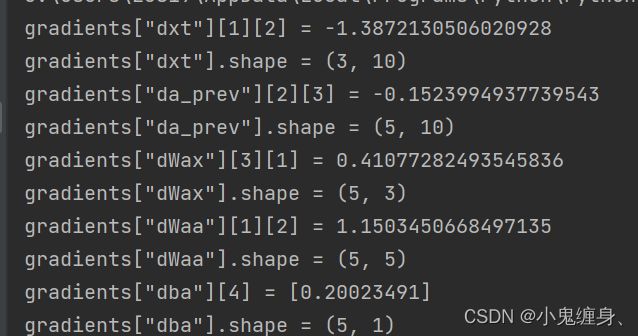
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
import numpy as np
import torch.nn
# GRADED FUNCTION: rnn_forward
# GRADED FUNCTION: rnn_cell_forward
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
def rnn_cell_forward(xt, a_prev, parameters):
"""
Implements a single forward step of the RNN-cell as described in Figure (2)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
"""
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ### (≈2 lines)
# compute next activation state using the formula given above
a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
# compute output of the current cell using the formula given above
yt_pred = softmax(np.dot(Wya, a_next) + by)
### END CODE HERE ###
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
def rnn_cell_backward(da_next, cache):
"""
Implements the backward pass for the RNN-cell (single time-step).
Arguments:
da_next -- Gradient of loss with respect to next hidden state
cache -- python dictionary containing useful values (output of rnn_step_forward())
Returns:
gradients -- python dictionary containing:
dx -- Gradients of input data, of shape (n_x, m)
da_prev -- Gradients of previous hidden state, of shape (n_a, m)
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dba -- Gradients of bias vector, of shape (n_a, 1)
"""
# Retrieve values from cache
(a_next, a_prev, xt, parameters) = cache
# Retrieve values from parameters
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ###
# compute the gradient of tanh with respect to a_next (≈1 line)
dtanh = (1 - a_next * a_next) * da_next # 注意这里是 element_wise ,即 * da_next,dtanh 可以只看做一个中间结果的表示方式
# compute the gradient of the loss with respect to Wax (≈2 lines)
dxt = np.dot(Wax.T, dtanh)
dWax = np.dot(dtanh, xt.T)
# 根据公式1、2, dxt = da_next .( Wax.T . (1- tanh(a_next)**2) ) = da_next .( Wax.T . dtanh * (1/d_a_next) )= Wax.T . dtanh
# 根据公式1、3, dWax = da_next .( (1- tanh(a_next)**2) . xt.T) = da_next .( dtanh * (1/d_a_next) . xt.T )= dtanh . xt.T
# 上面的 . 表示 np.dot
# compute the gradient with respect to Waa (≈2 lines)
da_prev = np.dot(Waa.T, dtanh)
dWaa = np.dot(dtanh, a_prev.T)
# compute the gradient with respect to b (≈1 line)
dba = np.sum(dtanh, keepdims=True, axis=-1) # axis=0 列方向上操作 axis=1 行方向上操作 keepdims=True 矩阵的二维特性
### END CODE HERE ###
# Store the gradients in a python dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
# GRADED FUNCTION: rnn_forward
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)
da_next = np.random.randn(5,10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
gradients["dxt"][1][2] = -0.4605641030588796
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = 0.08429686538067724
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.39308187392193034
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = -0.28483955786960663
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [0.80517166]
gradients["dba"].shape = (5, 1)
下面对numpy和torch两个版本进行比较:
import torch
import numpy as np
class RNNCell:
def __init__(self, weight_ih, weight_hh,
bias_ih, bias_hh):
self.weight_ih = weight_ih
self.weight_hh = weight_hh
self.bias_ih = bias_ih
self.bias_hh = bias_hh
self.x_stack = []
self.dx_list = []
self.dw_ih_stack = []
self.dw_hh_stack = []
self.db_ih_stack = []
self.db_hh_stack = []
self.prev_hidden_stack = []
self.next_hidden_stack = []
# temporary cache
self.prev_dh = None
def __call__(self, x, prev_hidden):
self.x_stack.append(x)
next_h = np.tanh(
np.dot(x, self.weight_ih.T)
+ np.dot(prev_hidden, self.weight_hh.T)
+ self.bias_ih + self.bias_hh)
self.prev_hidden_stack.append(prev_hidden)
self.next_hidden_stack.append(next_h)
# clean cache
self.prev_dh = np.zeros(next_h.shape)
return next_h
def backward(self, dh):
x = self.x_stack.pop()
prev_hidden = self.prev_hidden_stack.pop()
next_hidden = self.next_hidden_stack.pop()
d_tanh = (dh + self.prev_dh) * (1 - next_hidden ** 2)
self.prev_dh = np.dot(d_tanh, self.weight_hh)
dx = np.dot(d_tanh, self.weight_ih)
self.dx_list.insert(0, dx)
dw_ih = np.dot(d_tanh.T, x)
self.dw_ih_stack.append(dw_ih)
dw_hh = np.dot(d_tanh.T, prev_hidden)
self.dw_hh_stack.append(dw_hh)
self.db_ih_stack.append(d_tanh)
self.db_hh_stack.append(d_tanh)
return self.dx_list
if __name__ == '__main__':
np.random.seed(123)
torch.random.manual_seed(123)
np.set_printoptions(precision=6, suppress=True)
rnn_PyTorch = torch.nn.RNN(4, 5).double()
rnn_numpy = RNNCell(rnn_PyTorch.all_weights[0][0].data.numpy(),
rnn_PyTorch.all_weights[0][1].data.numpy(),
rnn_PyTorch.all_weights[0][2].data.numpy(),
rnn_PyTorch.all_weights[0][3].data.numpy())
nums = 3
x3_numpy = np.random.random((nums, 3, 4))
x3_tensor = torch.tensor(x3_numpy, requires_grad=True)
h3_numpy = np.random.random((1, 3, 5))
h3_tensor = torch.tensor(h3_numpy, requires_grad=True)
dh_numpy = np.random.random((nums, 3, 5))
dh_tensor = torch.tensor(dh_numpy, requires_grad=True)
h3_tensor = rnn_PyTorch(x3_tensor, h3_tensor)
h_numpy_list = []
h_numpy = h3_numpy[0]
for i in range(nums):
h_numpy = rnn_numpy(x3_numpy[i], h_numpy)
h_numpy_list.append(h_numpy)
h3_tensor[0].backward(dh_tensor)
for i in reversed(range(nums)):
rnn_numpy.backward(dh_numpy[i])
print("numpy_hidden :\n", np.array(h_numpy_list))
print("tensor_hidden :\n", h3_tensor[0].data.numpy())
print("------")
print("dx_numpy :\n", np.array(rnn_numpy.dx_list))
print("dx_tensor :\n", x3_tensor.grad.data.numpy())
print("------")
print("dw_ih_numpy :\n",
np.sum(rnn_numpy.dw_ih_stack, axis=0))
print("dw_ih_tensor :\n",
rnn_PyTorch.all_weights[0][0].grad.data.numpy())
print("------")
print("dw_hh_numpy :\n",
np.sum(rnn_numpy.dw_hh_stack, axis=0))
print("dw_hh_tensor :\n",
rnn_PyTorch.all_weights[0][1].grad.data.numpy())
print("------")
print("db_ih_numpy :\n",
np.sum(rnn_numpy.db_ih_stack, axis=(0, 1)))
print("db_ih_tensor :\n",
rnn_PyTorch.all_weights[0][2].grad.data.numpy())
print("------")
print("db_hh_numpy :\n",
np.sum(rnn_numpy.db_hh_stack, axis=(0, 1)))
print("db_hh_tensor :\n",
rnn_PyTorch.all_weights[0][3].grad.data.numpy())
"""
代码输出
numpy_hidden :
[[[ 0.4686 -0.298203 0.741399 -0.446474 0.019391]
[ 0.365172 -0.361254 0.426838 -0.448951 0.331553]
[ 0.589187 -0.188248 0.684941 -0.45859 0.190099]]
[[ 0.146213 -0.306517 0.297109 0.370957 -0.040084]
[-0.009201 -0.365735 0.333659 0.486789 0.061897]
[ 0.030064 -0.282985 0.42643 0.025871 0.026388]]
[[ 0.225432 -0.015057 0.116555 0.080901 0.260097]
[ 0.368327 0.258664 0.357446 0.177961 0.55928 ]
[ 0.103317 -0.029123 0.182535 0.216085 0.264766]]]
tensor_hidden :
[[[ 0.4686 -0.298203 0.741399 -0.446474 0.019391]
[ 0.365172 -0.361254 0.426838 -0.448951 0.331553]
[ 0.589187 -0.188248 0.684941 -0.45859 0.190099]]
[[ 0.146213 -0.306517 0.297109 0.370957 -0.040084]
[-0.009201 -0.365735 0.333659 0.486789 0.061897]
[ 0.030064 -0.282985 0.42643 0.025871 0.026388]]
[[ 0.225432 -0.015057 0.116555 0.080901 0.260097]
[ 0.368327 0.258664 0.357446 0.177961 0.55928 ]
[ 0.103317 -0.029123 0.182535 0.216085 0.264766]]]
------
dx_numpy :
[[[-0.643965 0.215931 -0.476378 0.072387]
[-1.221727 0.221325 -0.757251 0.092991]
[-0.59872 -0.065826 -0.390795 0.037424]]
[[-0.537631 -0.303022 -0.364839 0.214627]
[-0.815198 0.392338 -0.564135 0.217464]
[-0.931365 -0.254144 -0.561227 0.164795]]
[[-1.055966 0.249554 -0.623127 0.009784]
[-0.45858 0.108994 -0.240168 0.117779]
[-0.957469 0.315386 -0.616814 0.205634]]]
dx_tensor :
[[[-0.643965 0.215931 -0.476378 0.072387]
[-1.221727 0.221325 -0.757251 0.092991]
[-0.59872 -0.065826 -0.390795 0.037424]]
[[-0.537631 -0.303022 -0.364839 0.214627]
[-0.815198 0.392338 -0.564135 0.217464]
[-0.931365 -0.254144 -0.561227 0.164795]]
[[-1.055966 0.249554 -0.623127 0.009784]
[-0.45858 0.108994 -0.240168 0.117779]
[-0.957469 0.315386 -0.616814 0.205634]]]
------
dw_ih_numpy :
[[ 3.918335 2.958509 3.725173 4.157478]
[ 1.261197 0.812825 1.10621 0.97753 ]
[ 2.216469 1.718251 2.366936 2.324907]
[ 3.85458 3.052212 3.643157 3.845696]
[ 1.806807 1.50062 1.615917 1.521762]]
dw_ih_tensor :
[[ 3.918335 2.958509 3.725173 4.157478]
[ 1.261197 0.812825 1.10621 0.97753 ]
[ 2.216469 1.718251 2.366936 2.324907]
[ 3.85458 3.052212 3.643157 3.845696]
[ 1.806807 1.50062 1.615917 1.521762]]
------
dw_hh_numpy :
[[ 2.450078 0.243735 4.269672 0.577224 1.46911 ]
[ 0.421015 0.372353 0.994656 0.962406 0.518992]
[ 1.079054 0.042843 2.12169 0.863083 0.757618]
[ 2.225794 0.188735 3.682347 0.934932 0.955984]
[ 0.660546 -0.321076 1.554888 0.833449 0.605201]]
dw_hh_tensor :
[[ 2.450078 0.243735 4.269672 0.577224 1.46911 ]
[ 0.421015 0.372353 0.994656 0.962406 0.518992]
[ 1.079054 0.042843 2.12169 0.863083 0.757618]
[ 2.225794 0.188735 3.682347 0.934932 0.955984]
[ 0.660546 -0.321076 1.554888 0.833449 0.605201]]
------
db_ih_numpy :
[ 7.568411 2.175445 4.335336 6.820628 3.51003 ]
db_ih_tensor :
[ 7.568411 2.175445 4.335336 6.820628 3.51003 ]
------
db_hh_numpy :
[ 7.568411 2.175445 4.335336 6.820628 3.51003 ]
db_hh_tensor :
[ 7.568411 2.175445 4.335336 6.820628 3.51003 ]
"""
总结
通过此次对于BPTT的反向传播推导,之前一直有不理解的地方,然后又查了好多博客,看了看他们的推导,才写出来,当中发现他们推导的确是很细致和详细,我在参考文献中放入几个推导好的文章可以看一下。
References:
纯Python和PyTorch对比实现循环神经网络RNN及反向传播
循环神经网络RNNCell单元详解及反向传播的梯度求导手推
手推RNN反向传播
L5W1作业1 手把手实现循环神经网络
老师的博客:
NNDL 作业9:分别使用numpy和pytorch实现BPTT