GC-LSTM原理+代码(下)代码部分基于PyG Temporal
上一篇文章GC-LSTM原理部分中具体介绍了GC-LSTM的原理,这里基于PyG Temporal中的GCLSTM模块对实现一个基于GC-LSTM的预测模型。注:这里可以是流量预测等各种节点特征。
一、数据预处理
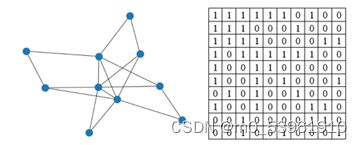
这里图拓扑的结构![]() 和邻接矩阵
和邻接矩阵![]()
![]() 如图所示,
如图所示,![]() :
:
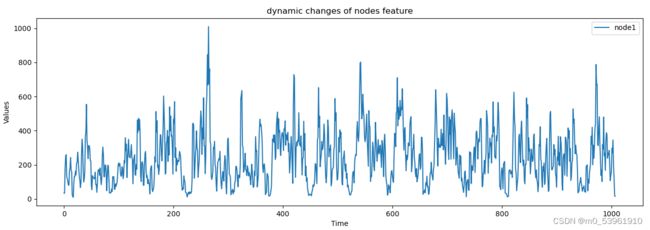
节点特征矩阵![]() ,这里只展示了其中一个节点的特征向量随时间的变化,只选取了一个指标即
,这里只展示了其中一个节点的特征向量随时间的变化,只选取了一个指标即![]() :
:
接下来我们需要对数据进行预处理,具体过程如代码所示:
def clean_train_test_data(traindata, testdata):
sc = MinMaxScaler(feature_range = (-1, 1))
# sc = StandardScaler()
train_data= sc.fit_transform(traindata)
test_data = sc.transform(testdata) # 利用训练集的属性对测试集进行归一化
return train_data, test_data
# 将数据划分为训练集与测试集,前80%的数据作为训练集,后20%的数据作为测试集
train_size = int(len(node_cpu)*0.8)
test_size = len(node_cpu) - train_size
train_data = node_cpu[0:train_size, :]
test_data = node_cpu[train_size:len(node_cpu), :]
train_data, test_data = clean_train_test_data(train_data, test_data)
# print(train_data.shape)(806, 10)
# print(test_data.shape)(202, 10)
train_data = np.array(train_data).transpose()
test_data = np.array(test_data).transpose()
# print(train_data.shape)#(10, 806)
def split_dataset(data, n_sequence, n_pre):
'''
对数据进行处理,根据输入模型的历史数据长度和预测数据长度对数据进行切分
:param data: 输入数据集
:param n_sequence: 历史数据长度
:param n_pre: 预测数据长度
:return: 划分好的train data和target data
'''
train_X, train_Y = [], []
for i in range(data.shape[1] - n_sequence - n_pre):
a = data[:, i:(i + n_sequence)]
train_X.append(a)
b = data[:, (i + n_sequence):(i + n_sequence + n_pre)]
train_Y.append(b)
# train_X = np.array(train_X)
# train_Y = np.array(train_Y)
return train_X, train_Y
history_data = 72
predict_data = 1
train_feature, train_target = split_dataset(train_data, history_data, predict_data)
test_feature, test_target = split_dataset(test_data, history_data, predict_data)
# print(train_feature.shape, train_target.shape)#(733, 10, 72) (733, 10, 1)
# print(test_feature.shape, test_target.shape)#(129, 10, 72) (129, 10, 1)
# 数据的邻接矩阵A
edge_index = np.array([[0, 1, 0, 2, 0, 3, 0, 4, 0, 5, 0, 7, 1, 2, 1, 6, 2, 3, 2, 8, 2, 9, 3, 4, 3, 5, 3, 6, 3, 7, 5, 9, 7, 8],
[1, 0, 2, 0, 3, 0, 4, 0, 5, 0, 7, 0, 2, 1, 6, 1, 3, 2, 8, 2, 9, 2, 4, 3, 5, 3, 6, 3, 7, 3, 9, 5, 8, 7]])
'''PyG Temporal中的类似DataLoader的数据处理器:
edge_index:是邻接矩阵;
edge_weight:是每个链路的权重;
features:是输入历史节点特征矩阵;
targets:是输入预测节点特征举证ground-truth;'''
train_dataset = StaticGraphTemporalSignal(edge_index=edge_index, edge_weight=np.ones(edge_index.shape[1]), features=train_feature, targets=train_target)
test_dataset = StaticGraphTemporalSignal(edge_index=edge_index, edge_weight=np.ones(edge_index.shape[1]), features=test_feature, targets=test_target)
# print("Number of train buckets: ", len(set(train_dataset)))#733
# print("Number of test buckets: ", len(set(test_dataset)))#129二、模型
这里是模型部分的代码,关于GCN的详细介绍和实现,GCN从0到1里面以及说的很详细了,这里不在过多赘述;关于GCN-LSTM模型的介绍,在这里。这里需要说明的一点是,GCN_LSTM中的input_size其实是数据经过GCN处理之后的output_size,也就是输入到LSTM中的input_size。
class GCN_LSTM(torch.nn.Module):
def __init__(self, node_features, input_size, output_size):
super(GCN_LSTM, self).__init__()
self.recurrent = GCLSTM(node_features, input_size, output_size)
self.MLP = torch.nn.Sequential(
torch.nn.Linear(input_size, input_size // 2),
torch.nn.ReLU(inplace=True),
torch.nn.Linear(input_size // 2, input_size // 4),
torch.nn.ReLU(inplace=True),
torch.nn.Linear(input_size // 4, output_size))
def forward(self, x, edge_index, edge_weight):
x, _ = self.recurrent(x, edge_index, edge_weight)
x = F.relu(x)
x = F.dropout(x, training=self.training)
x = self.MLP(x)
return x
model = GCN_LSTM(node_features=72, input_size=36, output_size=1)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=1.5e-3)
loss_mse = torch.nn.MSELoss()
cost_list = []
model.train()
'''time为train size'''
for epoch in tqdm(range(300)):
cost = 0
for time, snapshot in enumerate(train_dataset):
y_hat = model(snapshot.x, snapshot.edge_index, snapshot.edge_attr)
cost = cost + loss_mse(y_hat, snapshot.y)
cost = cost / (time + 1)
cost_list.append(cost.item())
cost.backward()
optimizer.step()
optimizer.zero_grad()
cost = cost.item()
print("training MSE: {:.4f}".format(cost))
plt.plot(cost_list)
plt.xlabel("Epoch")
plt.ylabel("MSE")
plt.title("average of Training cost for 10 nodes")
plt.show()
model.eval()
cost = 0
test_real = []
test_pre = []
cha = []
for time, snapshot in enumerate(test_dataset):
y_hat = model(snapshot.x, snapshot.edge_index, snapshot.edge_attr)
test_pre.append(y_hat.detach().numpy())
test_real.append(snapshot.y.detach().numpy())
cost = cost + torch.mean((y_hat - snapshot.y) ** 2)
cha_node = y_hat - snapshot.y
cha.append(cha_node.detach().numpy())
# print('cost', cost)
# print('cha', cha_node)
cost = cost / (time + 1)
cost = cost.item()
print("test MSE: {:.4f}".format(cost))
test_real = np.array(test_real)
test_real = test_real.reshape([test_real.shape[0], test_real.shape[2]])
test_pre = np.array(test_pre)
test_pre = test_pre.reshape([test_pre.shape[0], test_pre.shape[2]])
plt.figure(1)
for i in range(test_real.shape[1]):
plt.subplot(3, 4, 1+i)
plt.plot(test_real[:, i], label='real data')
plt.plot(test_pre[:, i], label='pre data')
plt.xlabel("Time steps")
plt.ylabel("Normalized Price")
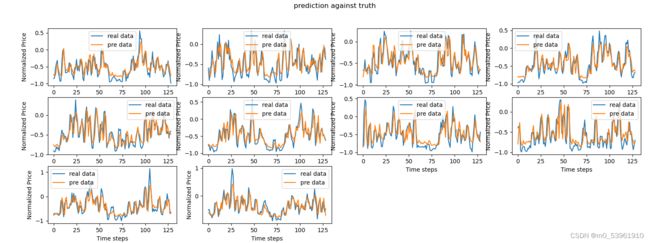
plt.suptitle("prediction against truth")
plt.legend()
plt.show()输出结果
损失函数:
预测结果: