matlab sym用法_MATLAB新手入门篇1(基础)
MATLAB是一个数学工具性软件,做数值分析很有用,而且相比较C类编程软件语言更加简单,用习惯后操作起来很便捷,尤其是它的三个界面(Command Window、Current Directory Workspace and Command History),在指令窗(Command Window)中输入指令,在工作空间浏览器(Workspace)中查看已有变量名、大小和字节数,很喜欢历史指令窗( Command History)重复输入的语句不用再指令窗中再打一遍可以由历史指令窗直接调出。
①下面是MATLAB入门基础中的基础:
计算语句:
>> (15*(177+68)-5)*3^2
ans =
33030语句换行:3个或3个以上连续的黑点表示续行,在下一行可以继续输入语句。例,
>> s=1-1/2+1/3-1/4+1/5-1/6+1/7-...
1/8+1/9-1/10
s =
0.6456变量名:对字母大小写敏感,第一个字符是英文字母,可以由字母数字和下连符构成,由以下语句判断是否与MATLAB自用变量名重复(零则不重复可以使用)。例,
>> exist cool
ans =
2
>> exist verygood
ans =
0②Matlab面向复数:复数可以由直角坐标表示和极坐标表示,real/imag/abs/angle分别计算复数的实部、虚部、模和幅角(弧度单位)。下面是这几个语句的例子,读者自行练习:
>> z1=2+3*i
>> z2=2*exp(pi/6*i)
>> z=z1*z2
>> rz=real(z)
>> iz=imag(z)
>> az=abs(z)
>> az1=angle(z)
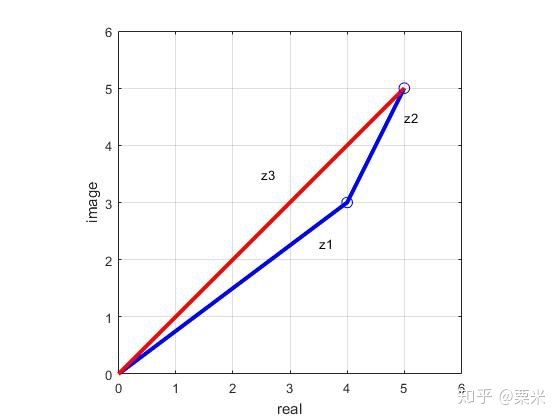
>> az2=angle(z)*180/pi %度数单位下面请读者自行选择练习:复数相加的几何意义、MATLAB可绘图功能。
>> z1=4+3*i;z2=1+2*i;
>> z3=z1+z2;
>> z3=z1+z2
>> plot([0,z1,z3],'-b','LineWidth',3)
>> plot([0,z3],'-r','LineWidth',3)
>> plot([0,z1,z3],'-b','LineWidth',3)
>> hold on
>> plot([0,z3],'-r','LineWidth',3)
>> plot([z1,z3],'ob','MarkerSize',8)
>> hold off,grid on,
>> axis equal
>> axis([0,6,0,6])
>> text(3.5,2.3,'z1')
>> text(5,4.5,'z2')
>> text(2.5,3.5,'z3')
>> xlabel('real')
>> ylabel('image')
>> shg理解
>> a=-27;
>> p=[1,0,0,-a];
>> r=roots(p)
r =
-3.0000 + 0.0000i
1.5000 + 2.5981i
1.5000 - 2.5981i③Matlab面向数组:矩阵的输入,例,
>> A=[1,3;2,4]
>> B=[1,3
2,4]数组的运算,以画衰减振荡曲线
>> t=0:pi/50:4*pi;
>> y=exp(-t/3).*sin(3*t);
>> plot(t,y,'-r','LineWidth',2)
>> axis([0,4*pi,-1,1])
>> xlabel('t'),ylabel('y')注意此处为数组乘法用点乘。
④MATLAB中符号计算:
定义符号对象sym或syms,后加‘positive’表示正数字符,后加‘real’表示实数字符。判断变量类型class,判断自由变量symvar,将指令化简为最简形式simplify
下面以求解
>> syms x
>> y=x^2+3*x+2;
>> x1=solve(y,x)
x1 =
-2
-1
>> f=(1/x^3+6/x^2+12/x+8)^(1/3)
f =
(12/x + 6/x^2 + 1/x^3 + 8)^(1/3)
>> g=simplify(f)
g =
((2*x + 1)^3/x^3)^(1/3)下面介绍subs用法:对函数赋值;转变函数变量,下面是该语句的例子,读者自行练习:
>> syms a b x;
>> f=a*sin(x)+b
>> f1=subs(f,a,3)
>> f2=subs(f,x,0:pi/2:pi)
f2 =
[ b, a + b, b]
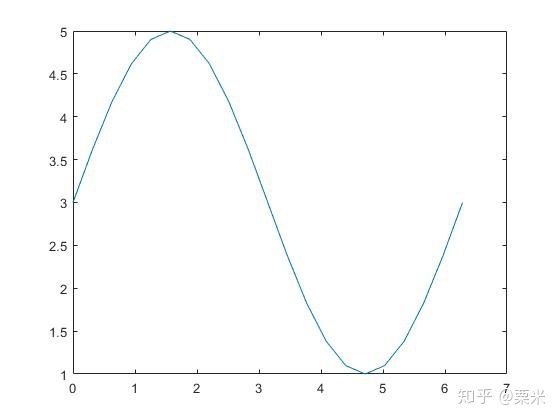
>> t=0:pi/10:2*pi;
>> f6=subs(f,{a,b,x},{2,3,t});
>> plot(t,f6)函数f对于变量x在a点求极限:limit(f,x,a);在a点求右极限limit(f,x,a,'right');在a点求左极限limit(f,x,a,'left')。函数f对于变量x求n阶导数:diff(f,x,n)。多元函数f对于自变量v=[x1,x2]求雅可比矩阵:jacobian(f,v)。一元函数f对于自变量x在a点的n-1阶泰勒展开式: taylor(f,x,a,'Order',n)。多元函数g对于变量x,y在[a,b]点的n-1阶泰勒展开式:taylor(g,[x,y],'ExpansionPoint',[a,b],'Order',n)。函数f在区间[a,b]对x求定积分:int(f,x,a,b)。
下面是这几个语句的例子,读者自行练习:
>> syms f k t x;
>> f=sin(k*t)/(k*t);
>> g=(1-1/x)^(k*x);
>> f1=limit(f,t,0)
>> g1=limit(g,x,inf)
>> syms a;
>> f=[a,t^3;t*cos(x),log(x)];
>> d1=diff(f)
>> d2=diff(f,t,2)
>> d12=diff(diff(f,x),t)
>> syms x1 x2;
>> f=[x1*exp(x2);x2;cos(x1)*sin(x2)];
>> v=[x1;x2];
>> Jf=jacobian(f,v)
>> f=x*exp(x)
>> g=taylor(f,x,0,'Order',8)
>> clear
>> syms x y
>> g=sin(x^2+y);
>> tg=taylor(g,[x,y],'ExpansionPoint',[0,0],'Order',6)
>> syms x positive
>> syms y z
>> F=int(int(int(x^2+y^2+z^2,z,sqrt(x*y),x^2*y),y,sqrt(x),x^2),x,1,2);
>> F1=vpa(F)