Multiscale Vision Transformers 论文阅读

附：论文地址，代码地址

一.了解MViT

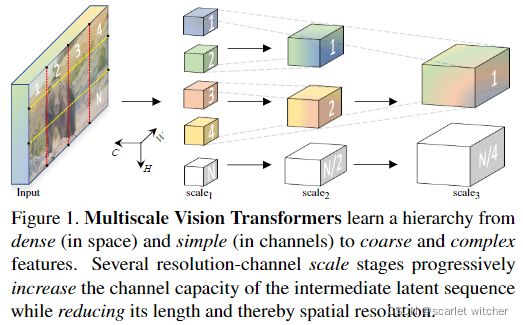
本文提出用于视频和图像识别的多尺度视觉变换器（Multiscale Vision Transformers），它将多尺度特征层次的基本思想与变换器模型相结合。

多尺度变换器具有多个通道和分辨率的缩放级，从输入的空间分辨率和较小的通道维度开始，分层扩展通道维度，同时降低空间分辨率。这将创建一个多尺度特征金字塔，前期的层以高空间分辨率操作，模拟简单的低级视觉信息，之后在空间粗糙但复杂的高维特征上创建更深的层。本文经过评估这一基本架构，发现其胜过大部分依赖外部预训练的模型（在计算和参数中比MViT多5-10倍）。

大致过程如下图所示

二.介绍MViT

1.基本思想

多尺度视觉变换器（MViT），是一种用于建模图像和视频等视觉数据的变换器体系结构。
由上面的图1所示，与在整个网络中保持恒定信道量和分辨率的传统变换器不同，MViT具有多个信道和分辨率缩放级。从输入的分辨率和较小的通道维度开始，阶段分层扩展通道容量，同时降低空间分辨率。有效地将transformer与多尺度特征层次结合起来。

2.优势

• 视觉信号的极度密集性。前期层信道容量较轻，可以在高空间分辨率下运行，模拟简单的低级视觉信息。反过来，深层可以关注复杂的高级特征。

• 多尺度模型充分利用时间信息。在自然视频上训练的ViT在具有混洗帧的视频上测试时，不会出现性能衰减，表明这些模型没有有效地使用时间信息，而是严重依赖于外观。相比之下，当在随机帧上测试MViT模型时，有显著的精度衰减，这表明十分依赖于时间信息。

• 本文的重点是视频识别，MViT使用数据集训练（(Kinetics ,Charades , SSv2 and AVA ）。MViT在没有任何外部预训练数据的情况下，相较于并发视频转换器有显著的性能提升。

• 与其他有外部预训练的模型相比（ViT的变体：VTN , TimeSformer ,ViViT ），达到相同的准确度具有更少的浮点计算和参数。

三.MViT模型

多尺度视觉变换器架构建立在阶段的概念之上。每一阶段由多个具有特定时空分辨率和通道尺寸的变换器块组成。多尺度变换器的主要思想是逐步扩展信道容量，同时汇集网络输入到输出的分辨率。

1.多头池化注意力（Multi Head Pooling Attention）

首先对MHPA作出解释，这是本文的核心，它使得多尺度变换器以逐渐变化的时空分辨率进行操作。与原始的多头注意力（MHA）不同，在原始的多头注意力中，通道维度和时空分辨率保持不变，MHPA将潜在张量序列合并，以减少参与输入的序列长度（分辨率）。如图3所示

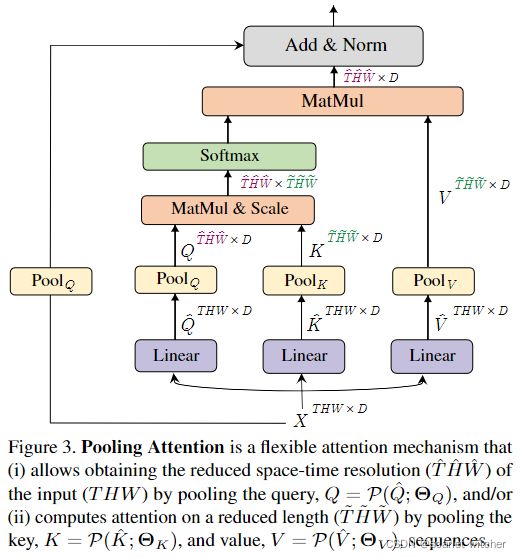
具体来说，一个D维的输入X，序列长度为L，$X\in {\mathbb{R}}^{L\ast D}$, MHPA 将输入X投影到$\hat{Q}\in {\mathbb{R}}^{L\ast D}$，$\hat{K}\in {\mathbb{R}}^{L\ast D}$，$\hat{V}\in {\mathbb{R}}^{L\ast D}$上

使用维数为D×D的权重W_Q、W_K、W_V ,然后使用池操作符 P将获得的中间张量按序列长度进行合并，下一节介绍池操作。

Pooling Operator
在参与输入之前，中间张量$\hat{Q}$，$\hat{K}$，$\hat{V}$参与运算符$P(\cdot ;\Theta )$，这是MHPA的基石，也是多尺度变换器架构的基础。运算符$P(\cdot ;\Theta )$沿每个维度对输入张量执行池化计算。$\Theta =（k，s，p）$，使用大小为 k_T×k_H×k_W 的池核k、大小为 s_T×s_H×s_W 的步长s和大小为p_T×p_H×p_W 的填充p,来减少尺寸L=T×H×W的输入张量,经过下面的公式池化之后

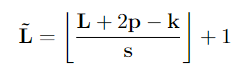
该公式是对每个维度进行计算，即将T，H，W分别进行计算得到$T$，$H$，$W$，将池化后的打平，就得到了 $P(Y;\Theta )\in {\mathbb{R}}^{L\ast D}$

一般情况下，在池化操作中，采用重叠的核k和保形填充p，使得最后得到的$P(Y;\Theta )$整体上缩减s_T s_H s_W

Pooling Attention
$P(\cdot ;\Theta )$ 分别地应用于所有中间张量$\hat{Q}$，$\hat{K}$，$\hat{V}$，由此产生预注意向量$Q=P（\hat{Q}；{\Theta }_Q）、K=P（\hat{K}；{\Theta }_K）和V=P（\hat{V}；{\Theta }_V）$。通过操作对Q，K，V进行计算

其中$\sqrt{D}$ 是按行对内积矩阵进行规范化。因此，随着$P(\cdot ;\Theta )$中查询向量 Q 的缩减，最后的输出结果是输出序列缩减了s_T^Q s_H^Q s_W^Q 。并且我们从图3可以注意到，s_k = s_v 必须成立，因为他们缩减的幅度必须一致，否则不能进行计算。

总结，以上公式可以用下面的公式来详细表达

Multiple heads
假设有h个头部，计算可以并行化，其中每个头部在D维输入张量X的D/h的非重叠子集上执行池化注意力。

2.多尺度变换器网络(Multiscale Transformer Networks)

基于多头集中注意力（MHPA），本文创造了专门使用MHPA和MLP层进行视觉表征学习的多尺度变换器模型。在此之前，了解一下ViT模型

2.1 Vision Transformer (ViT)

1. 首先将分辨率为 T × H × W 的输入视频，其中 T 为帧数、 H 为高度、 W 为宽度，分割成尺寸为1 × 16 × 16的非重叠块，然后在平坦图像块上逐点运用线性层，将其投影到潜在尺寸 D 中。就是1 × 16 × 16的核大小和步长的卷积，如表1中patch1阶段所示
   
2. 位置嵌入$E\in {\mathbb{R}}^{L\ast D}$ 添加到长度为L且维数为D的投影序列的每个元素。
3. 通过N个变换器块的顺序处理，产生的长度为L+1的序列，每个变换器块执行注意力（MHA）、多层感知机（MLP）和层规范化（LN）操作。通过以下公式计算：
   
   此处产生长度为L+1的序列是因为spacetime resolution + class token
4. N个连续块之后的结果序列被层规范化，通过线性层来预测输出。此处需要注意，默认情况下，MLP的输入是4D。

2.2 Multiscale Vision Transformers (MViT)

逐步增加信道维度，同时降低整个网络的时空分辨率（即序列长度）。MViT在早期层中具有精细的时空分辨率和低信道维度，而在后期层中，变为粗略的时空分辨率和高信道维度。MViT如表2所示。

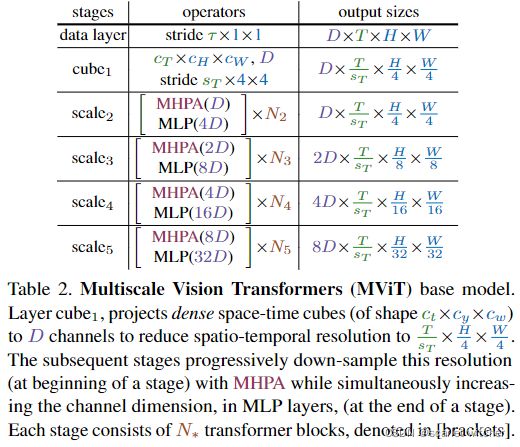
Scale stages
尺度阶段定义为一组N个变换器块，在相同的尺度上跨信道和时空维度以相同的分辨率运行。在阶段转换时，信道维度上采样，而序列的长度下采样。

Channel expansion
当从一个阶段过渡到下一个阶段时，通过增加前一阶段最终MLP层的输出来扩展通道维数，增加的因素与该阶段引入的分辨率变化相关。举个例子来说，时空分辨率降低4倍，那么通道维数需要增大2倍。

Query pooling
池操作使得查询向量方面有更高的灵活性，从而可以改变输出序列的长度。将查询向量 $P(Q;k;p;s)$与核函数 s ≡(s^Q_T，s^Q_H，s^Q_W)结合起来，使序列减少了 s^Q_T，s^Q_H，s^Q_W。这里有个点需要注意，一个阶段的开始降低分辨率，然后在整个阶段保持分辨率，所以只有每个阶段的第一个P在 s^Q > 1，其他都是 s^Q ≡(1,1,1)

Key-Value pooling
与查询池不同，更改键K和值V张量的序列长度不会更改输出序列长度（时空分辨率），所以对于所有的K和V都执行了池化。上面说过，最后为了能够执行计算，K和V池化后的各个维度必须一致，所以本文默认情况下，取${\Theta }_K\equiv {\Theta }_V$

Skip connections
由于通道尺寸和序列长度发生变化，对skip connection 进行pool 以适应其两端的尺寸不匹配。由图3可以看出，MHPA通过使用查询池操作符$Q=P（\hat{Q}；{\Theta }_Q）$来处理这种不匹配。

四.视频识别实验

• 数据集：Kinetics-400 和 Kinetics-600，记录了验证集的top-1和top-5分类准确率(%)、单个空间中心裁剪clip的计算成本(单位为FLOPs)以及使用的clip数量。
• 训练：默认情况下，所有模型都是在 Kinetics 上从随机初始化(“从头开始”)进行训练，而不使用 ImageNet或其他预训练。从全视频中取样一个clip，输入到网络的是一个时间跨度为 $\tau$ 的 $T$ 帧，表示为 $T\times \tau$
• 推理：
  （1） 在时间上，从视频中均匀采样K个clip（例如，K=5），将较短的空间侧缩放到256像素，并进行224×224的中心裁剪
  （2）与（1）在时间上相同，但进行3次224×224的裁剪以覆盖较长的空间轴，对所有个体预测的得分取平均值

1.Kinetics-400

表4将结果分为四部分，接下来依次对这四部分作简要介绍
第一部分是之前的方法，采用的是卷积网络所得到的结果。
第二部分是使用ViT。这种方法都依赖于ImageNet预先训练的基础模型。ViT-B-VTN从ImageNet-1K更改为ImageNet-21K，可将精度提高至78.6%。而ViViT有更为巨大的参数量，进一步提高精度。
第三部分显示了ViT基线。首先列出的ViT-B，是在ImageNet-21K上预先训练的，它达到79.3%，这一结果表明，简单地微调ImageNet-21K中现成的ViT-B模型可以提供一个良好的基线。
第四部分是MViT的结果。所有的模型都是从头开始训练的。轻量级MViT-S的为76.0%，MViT-B在相同设置下比ViT-B的精度提升9.9%，同时具有更少的FLOPs和参数量。将帧采样从16×4更改为32×3时，性能将提高到80.2%。

2.Kinetics-600

从头开始训练MViT，没有任何预训练。MViT通过5-clip，中心裁剪测试实现了83.4%的最先进水平，同时与依赖大规模ImageNet-21K预训练的ViT-L-ViViT相比，其FLOPs和参数量减少了56.0倍和8.4倍

3.Kinetics-400的消融实验

在Kinetics-400（K400）上进行消融实验，使用5-clip中心224×224作测试。展示了top-1精度以及空间大小为224×224的单个clip输入的计算复杂度（以GFLOPs为单位）。当使用固定数量(5个clip)时，推断计算成本成比例（用T×$\tau$=16×4采样）。报告了批量大小为4的参数量和训练GPU的内存。默认情况下，所有MViT均为MViT-B，T×$\tau$=16×4，MHSA中采用最大池化

Frame shuffling

可以从表9中看出，对于打乱的帧，MViT-B的精度下降严重，而ViT-B的精度几乎没有下降，可以得出ViT-B几乎没有用到时间信息，而MViT-B严重依赖时间信息。

Two scales in ViT

通过使用s_Q执行池化来实现这一点，s_Q ≡（1,2,2)。表10显示了结果,在ViT-B基线上增加单个分辨率缩放可将精确度提高+1.5%，同时将FLOPs和内存成本分别降低38%和41%。合并键值张量可以减少计算和内存开销，同时略微提高准确性。

Separate space & time embeddings in MViT

Input Sampling Rate

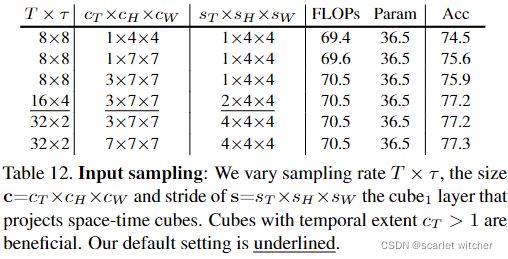
c_T=1的性能比c_T>1的性能差。此外，采样两倍的帧（T=16）和两倍的s_T（s_T = 2），可以保持成本（FLOPs和参数量）不变，但性能提高。此外，采样重叠的cube（s1有帮助，但是非常大的内核大小（cT=7）并不能进一步提高性能。

Stage distribution

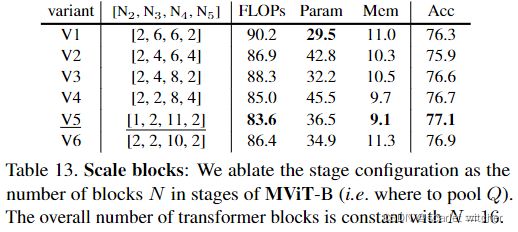
在变换器块数固定，N=16时，通过实验发现在scale4阶段放置更多的块数，有利于准确度的提高。

Key-Value pooling

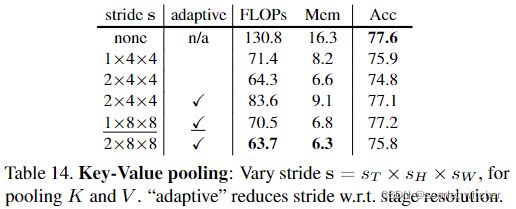
比较了使用无K、V池，无自适应池（关于stage resolution的stride）的基线和所有阶段固定步幅为2×4×4：这将准确性从77.6%降低到74.8%，在scale1阶段使用1×8×8、scale2阶段使用1×4×4、scale3阶段使用1×2×2的自适应步幅，可获得77.2%的最佳精度。

Pooling function

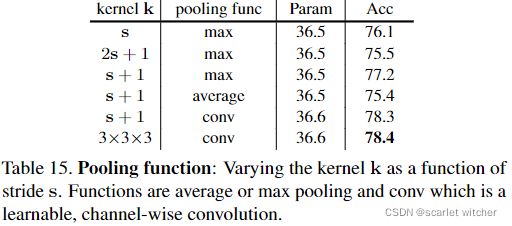
从表15得出，比较了不同的池化函数和核大小对于准确度的影响，可以看出卷积池化（本质就是卷积层）得到的准确率最高。并且使用max池化时，过大于stride的核不利于准确度的进一步提高。

Speed-Accuracy tradeoff

MViT-S和MViT-B模型不仅比ViT-B模型和卷积模型更准确，而且速度更快。在MViT中，由于卷积更新更多的参数，所以准确率高，但速度较max-pool慢。可以看出速度和准确率不可兼得。

五.小结

• 多尺度视觉变换器，将多尺度特征层次的概念与transformer结合起来
• MViT 层次化地扩展了通道维数，同时减少了时空分辨率。