4D 语义分割——TemporalLidarSeg
TemporalLidarSeg(3DV 2020) 主要贡献:
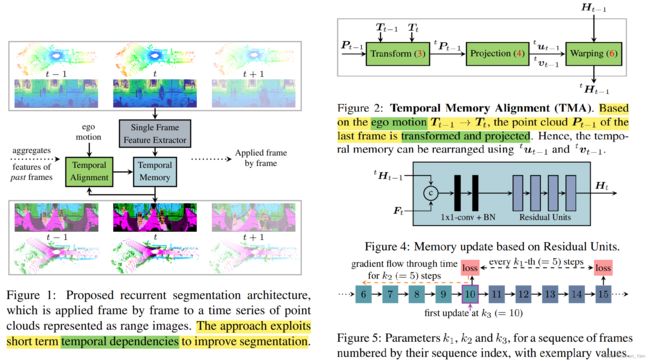
- 提出一种用于时间序列点云的循环分割体系结构(recurrent segmentation architecture),并利用时间依赖性(temporal dependencies)来提高分割结果
- 提出一种时间记忆对齐(Temporal Memory Alignment)策略,直接在 range 图像特征空间的相邻帧之间对齐时间记忆的特征
- 提出一种利用非均匀激光分布(laser distribution)的传感器广义 range 视角投影
文章目录
- 前言
- 网络结构
-
- Adaptive Range Image
- TMA
- Fusion Architecture
-
- Single Frame Backbone (SFB)
- Temporal Memory
前言
理解和解释 3D 环境是自动驾驶面临的一个关键挑战,而三维点云的语义分割结合了三维信息和语义,因此为这一任务提供了有价值的贡献。在许多实际应用中,点云是由激光雷达传感器在连续的时间中生成的。所以,通过时间序列(time series)而不是单一的框架可以利用这些时间信息,从而在一定程度上提高语义分割的精度。
基于此,论文提出了一种循环分割体系结构,它以一个 range 图像帧作为输入并利用递归聚合(recursively aggregated)的时间信息。为了有效重用前一帧的特征,论文提出了一种时间记忆对齐(TMA)策略,其使用 ego motion 来对齐特征空间中连续帧之间的记忆。此外,论文还研究了残差网络和 ConvGRU 对内存更新的影响。
论文作者在两个大型数据集上验证了所提出方法的优点,并将其与几种 SOTA 方法进行了比较。论文的方法在 SemanticKITTI 多扫描(multiple scan)基准测试中排名第一,在单扫描(single scan)基准测试中达到了 SOTA 的性能。此外,评估结果表明,与单帧方法相比,利用时间信息能显著地提高了分割结果。
网络结构
通常情况下,环境很少在短时间内发生剧烈变化,这导致两个相邻的点云帧共享大量信息,即之前的帧仍然包含有价值的信息,但这些信息会随着时间的增加而减少。因此,特别是短期的时间信息或依赖对当前帧分割结果的改善有着巨大的潜力。此外,由于没有考虑运动物体的运动,TMA 对运动的物体会产生系统误差。
论文提出的循环分割架构如 Fig. 1 所示。其中,每一帧的特征提取由一个单帧特征提取器(single frame feature extractor)进行;通过对这些特性递归地更新时间记忆,可利用相邻帧的时间依赖,且 TMA 步骤可确保帧之间的一致性。由于它的周期性,之前的帧信息可以持续有效地重用。
- TMA 需要先将上一帧点云进行转换和投影,然后再根据俯仰角和偏转角获取 range 图像中的像素,接着再进行索引操作(具体细节在后面章节
TMA中) - 记忆更新采用两种策略,分别使用残差单元和门控机制(具体细节在后面章节
Temporal Memory中) - 损失的反向传播采用
TBPTT,对 TBPTT 感兴趣可参考这篇博客。具体上讲,当处理到 k 1 k_1 k1 个时间步时,会使用 BPTT 反向传播 k 2 k_2 k2个 时间步。此外,为了让记忆在更新之前聚合到有意义的时间信息,第一次更新至少延迟到 k 3 k_3 k3 步。论文选择 k 1 = k 2 = 5 k_1 = k_2 = 5 k1=k2=5, k 3 = 10 k_3 = 10 k3=10
Adaptive Range Image
论文提出的框架采用 range 图像作为输入,因此,需要将点云进行投影操作。对球面投影感兴趣可参考这篇博客,球面投影公式如下:
( u v ) = ( ⌊ ( 1 − ( θ + f u p ) f − 1 ) ⋅ h ⌋ ⌊ 0.5 ⋅ ( 1 − ϕ ⋅ π − 1 ) ⋅ w ⌋ ) , ( 1 ) \begin{aligned} \begin{pmatrix} u \\ v \end{pmatrix} = \begin{pmatrix} \lfloor (1-(\theta+f_{up})f^{-1}) \cdot h \rfloor \\ \lfloor 0.5 \cdot (1- \phi \cdot \pi^{-1}) \cdot w \rfloor \end{pmatrix}, & \quad (1) \end{aligned} (uv)=(⌊(1−(θ+fup)f−1)⋅h⌋⌊0.5⋅(1−ϕ⋅π−1)⋅w⌋),(1)
✍️其中, ( u , v ) (u, v) (u,v) 是图像坐标系, ( h , w ) (h, w) (h,w) 为图像的分辨率(缩放因子); f u p f_{up} fup 为激光雷达上部视场, f d o w n f_{down} fdown 为激光雷达下部视场,而激光雷达视场 f = f u p − f d o w n f=f_{up} - f_{down} f=fup−fdown;对于点 ( x , y , z ) (x, y, z) (x,y,z),其到激光雷达的距离为 r = x 2 + y 2 + z 2 r=\sqrt{x^2 + y^2 + z^2} r=x2+y2+z2,而俯仰角 θ = a r c s i n z r \theta=arcsin \frac{z}{r} θ=arcsinrz,偏转角 ϕ = a r c t a n y x \phi=arctan\frac{y}{x} ϕ=arctanxy。
如果激光雷达的垂直堆叠激光(vertically stacked lasers)不是均匀分布的(像 PandaSet 使用的传感器那样),就会导致仰角分布不均匀。因此,使用上面的投影公式会导致许多碰撞(collisions),即可能有多个点被映射到 range 图像的同一像素上。这不仅意味着信息的丢失,而且还意味着对阴影点(shadowed points)预测的缺失。为了减少碰撞次数,论文提出了一种自适应的投影策略。其中,range 图像中的每一行 l ∈ [ 0 , h − 1 ] l \in [0, h-1] l∈[0,h−1] 对应垂直叠加中的一个激光(如 64 线激光雷达对应的 h h h 就为 64),并且每个激光都具有俯仰角(elevation angle) θ ‾ l \overline{\theta}_l θl。为解决非均匀性问题,需要指定俯仰角匹配最近的行,其公式为:
u = a r g m i n 0 ≤ l < h ( ∣ θ ‾ l − θ ∣ ) , ( 2 ) \begin{aligned} u = \underset{0 \le l \lt h}{argmin}(| \overline{\theta}_l - \theta |), & \quad (2) \end{aligned} u=0≤l<hargmin(∣θl−θ∣),(2)
接着根据计算得到的图像坐标,将 r r r、 x x x、 y y y、 z z z 以及缓解(remission) e e e 和占用标志(occupancy flag)映射到一个 6 × h × w 6 \times h \times w 6×h×w 的 range 图像中。
此外,ego motion 和角度的不确定性也会导致映射碰撞,这是论文所提出的映射无法避免的。因此,仍然需要一个基于标记点的后处理步骤来计算阴影点的类标签。根据 RangeNet++ ,论文使用 k k k 个最近邻的多数投票来确定缺失的标签。3D 点的邻居候选对象是 5×5 窗口中的像素,然后根据范围 r r r 选择 k k k 个最近邻,具体细节可参考 RangeNet++。
TMA
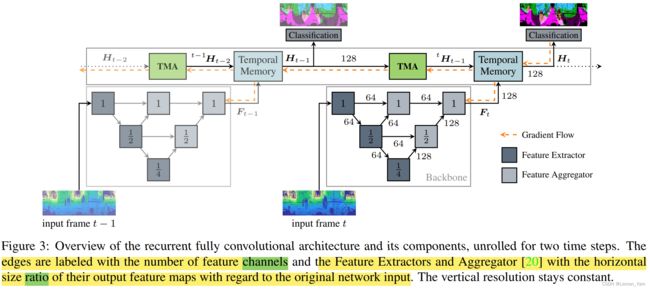
为了有效重用前一帧的特征,需要在 range 图像空间中对特征进行时间对齐。此外,由于 ego motion 导致传感器参考系统(reference system)通常在两帧之间移动,因此校准是必要的。虽然相机图像特征通常使用光流对齐,但论文提出了一种不同的对齐策略,这种策略可以在 2D 的 range 图像中利用点的笛卡尔坐标 p p p 和 ego motion。其过程如上图 Fig. 2,对于记录了相对于上一帧传感器位姿 T t − 1 \pmb{T}_{t−1} TTt−1 转换为当前帧传感器位姿 T t T_t Tt 的上一帧所有点 P t − 1 = ( p t − 1 0 , ⋯ , p t − 1 n ) = ( x t − 1 , y t − 1 , z t − 1 ) T \pmb{P}_{t-1} = (\pmb{p}^0_{t-1}, \cdots , \pmb{p}^n_{t-1}) = (\pmb{x}_{t-1}, \pmb{y}_{t-1}, \pmb{z}_{t-1})^T PPt−1=(ppt−10,⋯,ppt−1n)=(xxt−1,yyt−1,zzt−1)T,其计算公式如下:
t P t − 1 = T t − 1 ⋅ T t − 1 ⋅ P t − 1 , ( 3 ) \begin{aligned} ^{t}\pmb{P}_{t-1} = \pmb{T}^{-1}_t \cdot \pmb{T}_{t-1} \cdot \pmb{P}_{t-1}, & \quad (3) \end{aligned} tPPt−1=TTt−1⋅TTt−1⋅PPt−1,(3)
在此基础上,可获得变换后球面坐标的俯仰角和偏转角,从而得到图像坐标,其计算公式如下:
t θ t − 1 = a r c s i n ( t z t − 1 t r t − 1 ) ⇒ E q . 2 t u t − 1 t ϕ t − 1 = − a t a n 2 ( t y t − 1 , t x t − 1 ) ⇒ E q . 1 t v t − 1 ( 4 ) w i t h t r t − 1 = ( ∥ t p t − 1 0 ∥ , ⋯ , ∥ t p t − 1 n ∥ ) T \begin{aligned} & ^{t}\pmb{\theta}_{t-1} = arcsin(\frac{^{t}\pmb{z}_{t-1}}{^{t}\pmb{r}_{t-1}}) \overset{Eq.2}{\Rightarrow}\ ^{t}\pmb{u}_{t-1} \\ & ^{t} \pmb{\phi}_{t-1} = -atan2(^{t}\pmb{y}_{t-1}, ^{t}\pmb{x}_{t-1}) \overset{Eq.1}{\Rightarrow}\ ^{t}\pmb{v}_{t-1} & (4) \\ & with \ ^{t}\pmb{r}_{t-1} = (\parallel ^{t}\pmb{p}_{t-1}^0 \parallel, \cdots , \parallel ^{t}\pmb{p}_{t-1}^n \parallel)^T \end{aligned} tθθt−1=arcsin(trrt−1tzzt−1)⇒Eq.2 tuut−1tϕϕt−1=−atan2(tyyt−1,txxt−1)⇒Eq.1 tvvt−1with trrt−1=(∥tppt−10∥,⋯,∥tppt−1n∥)T(4)
✍️其中, a r c s i n arcsin arcsin、 a t a n 2 atan2 atan2 以及除法都是逐元素进行的,而 t u t − 1 ^{t}\pmb{u}_{t-1} tuut−1 和 t v t − 1 ^{t}\pmb{v}_{t-1} tvvt−1 描述了当前 range 图像帧中上一帧的测量值(measurements)和对应特征。对于特征的索引操作如下:
f u , v ← H [ u , v ] , f u , v ∈ R c , ( 5 ) \begin{aligned} \pmb{f}_{u, v} \leftarrow \pmb{H}[u, v], \quad \pmb{f}_{u, v} \in \mathbb{R}^c, & \quad (5) \end{aligned} ffu,v←HH[u,v],ffu,v∈Rc,(5)
✍️对于通道维度 c c c 和任意图像坐标 u u u 和 v v v,时间记忆(temporal memory) H \pmb{H} HH 的特征向量可以通过以下方式重新排列:
t H t − 1 [ t u t − 1 , t v t − 1 ] ← H t − 1 [ u t − 1 , v t − 1 ] ∀ t u t − 1 , t v t − 1 ∈ t u t − 1 , t v t − 1 ( 6 ) \begin{aligned} \begin{aligned} & ^{t}\pmb{H}_{t-1}[^{t}u_{t-1},\ ^{t}v_{t-1}] \leftarrow \pmb{H}_{t-1}[u_{t-1}, v_{t-1}] \\ & \forall \ ^{t}u_{t-1},\ ^{t}v_{t-1} \in \ ^{t}\pmb{u}_{t-1},\ ^{t}\pmb{v}_{t-1} \end{aligned} & \quad (6) \end{aligned} tHHt−1[tut−1, tvt−1]←HHt−1[ut−1,vt−1]∀ tut−1, tvt−1∈ tuut−1, tvvt−1(6)
Fusion Architecture
论文提出的结构主要利用来自前一帧的信息来改进语义分割的效果,其由**记忆对对齐(TMA)、单帧主干(SFB)和记忆模块( temporal memory)**这三个主要组件构成,且最后再通过 1×1 卷积和 softmax 层计算每一帧的预测,其结构如下所示:
Single Frame Backbone (SFB)
点云在前面步骤被处理成 range 图像并送到 backbone 中,backbone 为每一帧计算中间特征图。该 backbone 是基于 deep layer aggregation 的,且与 LaserNet 的 backbone 较为相似。与 LaserNet 相比,其唯一的区别是将前两个特征提取器中的残差单元分别减少到 4 和 5,并删除了第一个特征提取器中的下采样。
Temporal Memory
TemporalLidarSeg 的关键属性是它的循环结构,该结构支持随时间递归的信息聚合。不仅使用当前特征图 F t \pmb{F}_t FFt 进行语义分割,还使用包含来自过去的递归聚合信息的前一帧时间记忆 H t − 1 \pmb{H}_{t−1} HHt−1。论文研究了两种不同的记忆更新策略,分别应用于时间对齐记忆 t H t − 1 ^t\pmb{H}_{t−1} tHHt−1 和当前特征图 F t \pmb{F}_t FFt 来计算并更新的记忆 H t \pmb{H}_t HHt。
- Residual Network:该方法首先将时间对齐记忆 t H t − 1 ^t \pmb{H}_{t−1} tHHt−1 和来自 SFB 的中间特征图 F t \pmb{F}_t FFt 拼接起来,然后通过
1×1卷积层将特性通道数减半且后面跟着一个BN操作,最后使用四个残差单元来更新记忆 H t \pmb{H}_t HHt。 - Gated Recurrent Unit:第二个时间融合模块是一个使用门控机制(gating mechanisms)的
ConvGRU,ConvGRU 采用卷积层代替全连接层,以保持空间分辨率。通常情况下,GRU 比 LSTM 需要更少的内存和计算资源,且其性能与 LSTM 相近。其记忆更新依赖于卷积核 W z \pmb{W}_z WWz, W r \pmb{W}_r WWr, W \pmb{W} WW 和 U z \pmb{U}_z UUz, U r \pmb{U}_r UUr, U \pmb{U} UU,公式如下:
Z t = σ ( W z ∗ F t + U z ∗ t H t − 1 ) ( 7 ) R t = σ ( W r ∗ F t + U r ∗ t H t − 1 ) ( 8 ) H t ′ = t a n h ( W ∗ F t + U ∗ ( R t ∘ t H t − 1 ) ) ( 9 ) H t = ( 1 − Z t ) ∘ t H t − 1 + Z t ∘ H t ′ ( 10 ) \begin{aligned} \pmb{Z}_t & = \sigma(\pmb{W}_z * \pmb{F}_t + \pmb{U}_z *\ ^t \pmb{H}_{t-1}) & (7) \\ \pmb{R}_t & = \sigma(\pmb{W}_r * \pmb{F}_t + \pmb{U}_r *\ ^t \pmb{H}_{t-1}) & (8) \\ \pmb{H}^{'}_t &= tanh(\pmb{W} * \pmb{F}_t + \pmb{U} * (\pmb{R}_t \circ \ ^t\pmb{H}_{t-1})) & (9) \\ \pmb{H}_t &= (1-\pmb{Z}_t) \circ \ ^t\pmb{H}_{t-1} + \pmb{Z}_t \circ \pmb{H}^{'}_t & (10) \end{aligned} ZZtRRtHHt′HHt=σ(WWz∗FFt+UUz∗ tHHt−1)=σ(WWr∗FFt+UUr∗ tHHt−1)=tanh(WW∗FFt+UU∗(RRt∘ tHHt−1))=(1−ZZt)∘ tHHt−1+ZZt∘HHt′(7)(8)(9)(10)
✍️其中, ∘ \circ ∘ 为 Hadamard product, ∗ * ∗ 为卷积操作
论文地址:https://arxiv.org/pdf/2103.02263.pdf
代码地址:暂无