从零学习误差反向传播(梯度下降法)

一、基础知识

卷积神经网络中的参数存在于卷积核中，卷积核可以提取图像的特征，例如$\left[\begin{array}{ccc}1& 0& -1\\ 2& 0& -2\\ 1& 0& -1\end{array}\right]$就可以算出左右卷积核区域左右两边的差异。但对于下图中"5"这个数字的识别，我们很难说这个卷积核提取的特征是不是我们想要的，或是说这个特征能否让机器识别出"5"这个数字。

深度学习就可以根据损失函数和数据自动地去学习这些卷积核，从而提取网络自己认为的，最好的特征。

1.1损失函数

损失函数多种多样，流行的损失函数是衡量监督数据和输出数据的误差，从而拉近他们之间的距离。

y是网络输出的数据，全部加起来为1，说明输出时经过了softmax。
t为标签数据，这个标签标明了正确类是第三类。这样的表示方法称为one-hot表示法。

MSE

$MSE=\frac{1}{2}{\sum }_k(y_k-t_k{)}^2$
通过本公式计算可得结果为0.0975

cross entropy error

$E=-{\sum }_k{t}_{k}log{y}_k$
通过本公式计算可得结果为0.51

虽然在数值上两者相差较远，但实际上离正确结果越近，它们的值都是越小的。换句话来讲，只要是尽可能地让这两个损失函数小，那么一定会得到一个与标签相同的答案。

例如，在交叉熵中，$y$越大，$logy$就越接近0(负值)，整体就越接近0。

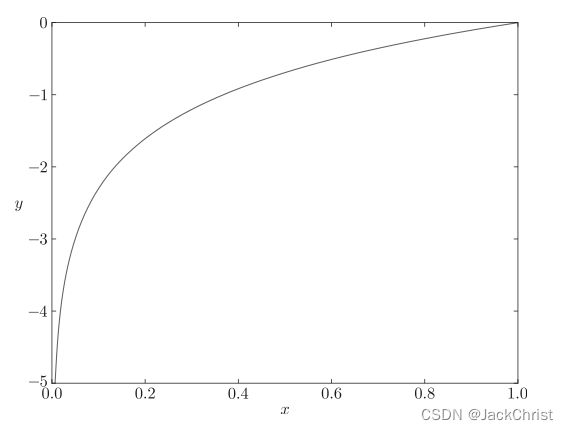
1.2数值微分

数值微分的意思就是将导数公式中的分母用尽可能小的数值去替代(因为实际上不可能极限趋于0)，一个替代的东西就会产生一定的误差。

$f$在$(x+h)$和$(x-h)$之间的差分称为中心差分(这样的差分)误差会小一些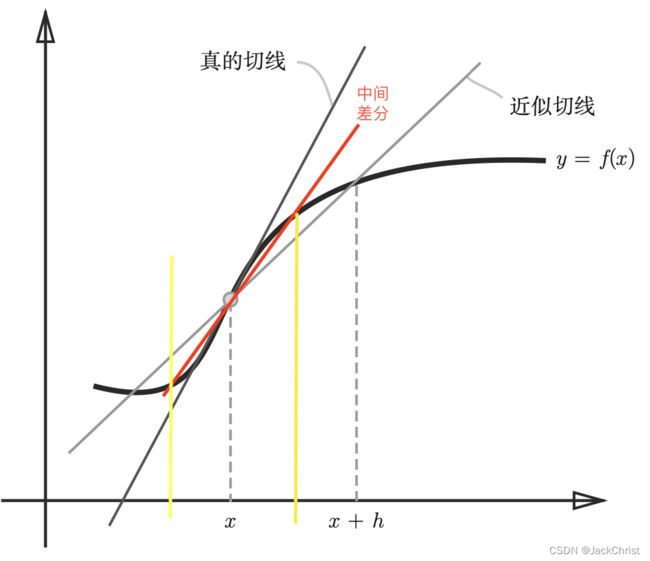

1.3偏导数

偏导数中不仅含有一个变量，而我们在求导时需要进行区分。
例如, $y=f(x_0,x_1)$，它具有两个变量。如图所示。

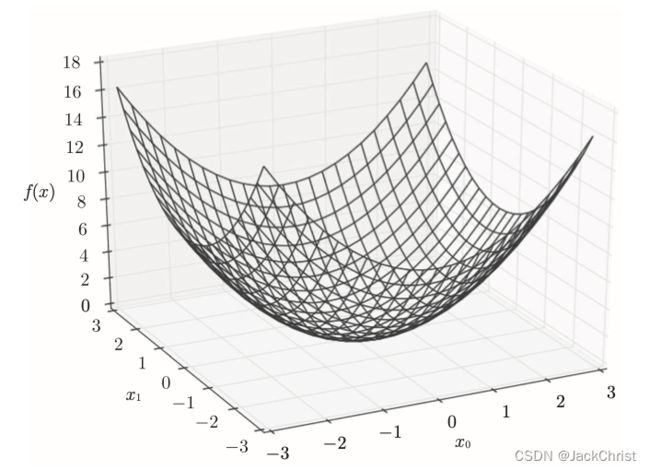
想要求偏导数也非常简单，在图中可以看到一个三维面，当确定一个值时，例如$x_0=0$，这个曲面就会变成一个曲线，这个曲线是$f(x_1)$的曲线。对于曲线的求导我们就会了，此时就在求偏导 $\frac{\partial f}{\partial x_1}$。

1.4梯度

由全部变量的偏导数汇总而成的向量称为梯度。
例如, $y=f(x_0,x_1)$，它的梯度为($\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1}$)

如果把这个函数每一个点的梯度画出来就如图所示。

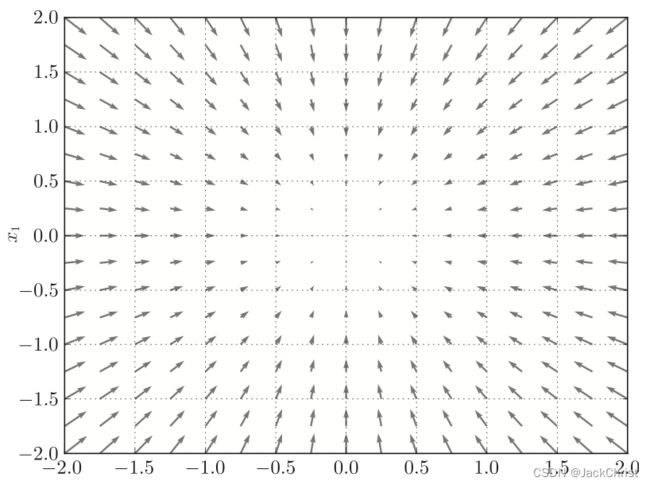
可以看出来，它们都指向一个方向（这是最理想化的情况），而这个方向是函数值减小最多的方向。
这是为什么呢，假设说我们有一个函数$f(x,y)$，还有一个任意方向 $l$。
对这个方向的偏导（方向导数）为如图所示。

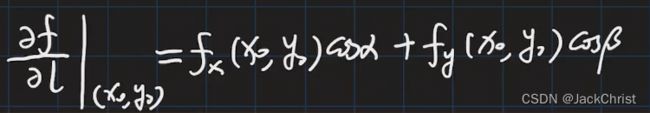
$\alpha$和$\beta$分别是是$l$与$x$和$y$方向的夹角，$cos$在[0,180]是递减的，也就是说与梯度方向一致时，$cos$的值是最大的，也就是最陡的，那同理负梯度方向就是这个陡坡（函数值下降最快的方向）。
但实际上，就算沿着某一点的陡坡去下降，也不一定能达到整个函数(损失函数)的最小值(这里就不赘述最小而极小的区别)，但每个点(每个权重)都去向着函数值会变小的方向移动，终归是较优的策略。

二、梯度下降法

$$\begin{gathered} x_0=x_0-\eta \frac{\partial f}{\partial x_0} \\ {x}_1=x_1-\eta \frac{\partial f}{\partial x_1} \end{gathered}$$
$\eta$表示学习率，也就是每一次学习(epoch)中，学习的幅度。
上式会随着训练反复进行，那么$x_0$和$x_1$在最终代入$f$中很有希望达到最小值，那么我们的目的就完成了。
代码如下：

import numpy as np

#定义一个函数
def function_1(x):
    f = x[0]**2 + x[1]**2
    return f

def n_d(f,x):
    h = 1e-4
    return (f(x+h) - f(x-h))/(2*h)

def numerical_gradient(f,x): #在数值偏导中，求x的偏导就给x增量
    h = 1e-4
    grad = np.zeros_like(x)
    #x很有可能有多个参数
    for i in range(len(x)):
        value = x[i]
        x[i] = value + h
        fxh1 = f(x)

        x[i] = value - h
        fxh2 = f(x)

        grad[i] = (fxh1 - fxh2)/(2*h)
        x[i] = value
    return grad


def gradient_descent(f,init,step):
    lr = 0.01
    x = init
    for i in range(step):
        grad = numerical_gradient(f,x)
        x -= lr*grad
    return x

init = np.array([-3.0,4.0])
res = gradient_descent(function_1,init,10000)
print(res)

2.1神经网络的梯度

ok，目前为止已经将二元函数的梯度以及它的下降介绍完，下面分析神经网络的梯度下降。
为了方便，这个公式就不打出来了。如图所示，也仅仅是2个未知数->6个未知数->n个，梯度也是同样的方法求得。

三、误差反向传播法

数值微分虽然简单，也容易实现，但缺点是计算上比较费时间。我们将学习一个能够高效计算权重参数的梯度的方法——误差反向传播法。

3.1 链式法则

假设 $$\begin{gathered} z=t^2 \\ t=x+y \end{gathered}$$

$z$对$x$求导可以用链式法则求，
$$\begin{gathered} \frac{\partial z}{\partial x}=\frac{\partial z}{\partial t}\frac{\partial t}{\partial x} \\ \frac{\partial z}{\partial x}=2t\ast 1=2(x+y) \end{gathered}$$
用计算图的方式表示出来，则如图所示

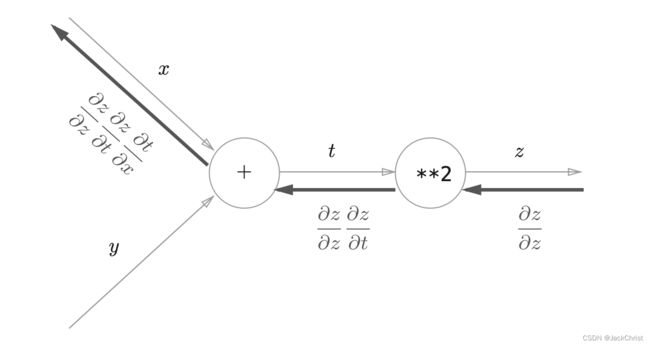
反向传播最开始的信号是$\frac{\partial z}{\partial z}=1$，如图走到x时，就通过过程化的形式表现出$\frac{\partial z}{\partial x}$的链式法则

3.2 反向传播

反向传播时没必要关心输入信号到底经历了什么样的复杂运算，仅仅关注于当前结点即可算出输出（下一个反向的输入）。
举例来讲，加法结点对输出未知数求偏导后肯定是1（前提是只有加法参与，事实上对于结点来讲肯定也只有一种运算的参与），所以只要经历加法结点，只需要原封不动地将上游的值输出到下游。

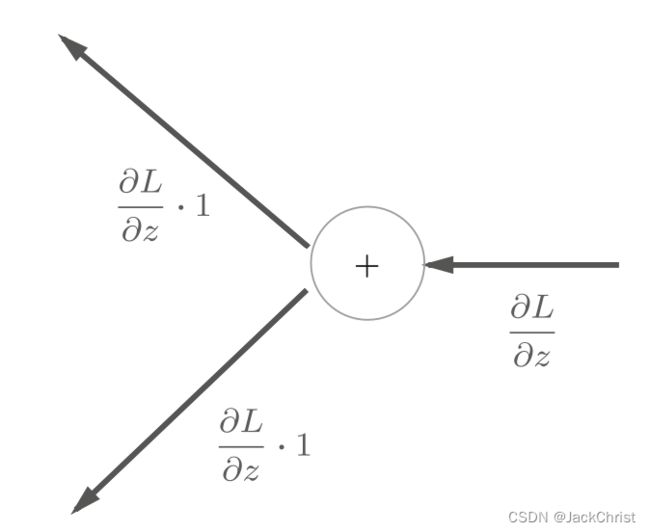
乘法结点考虑$z=xy$时，乘以正向传播时的翻转值，如图所示。

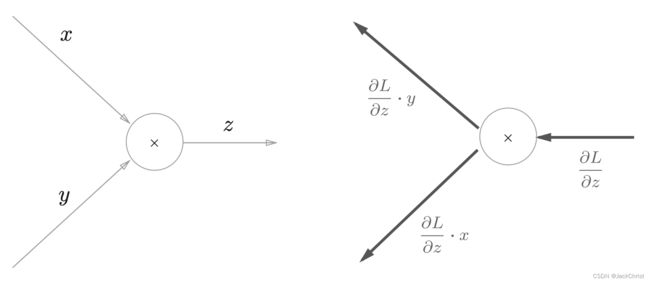
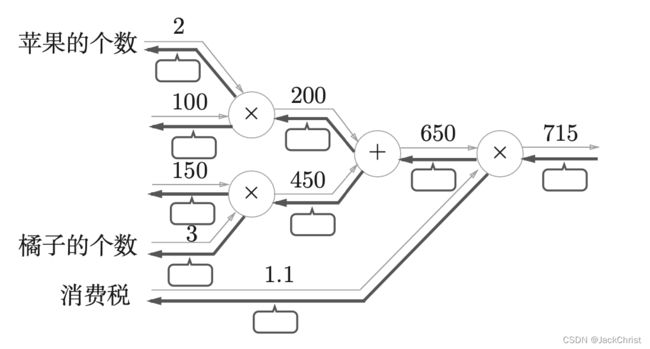
目前，我们可以做到给一张类似于下图的计算图，在方块中填入正确的数字。

但实际上神经网络并不知道加和乘法这么简单，我们能凭记忆去记的也就是寥寥几个。除了普通的运算操作，还有激活层的反向传播。

3.2.1激活层

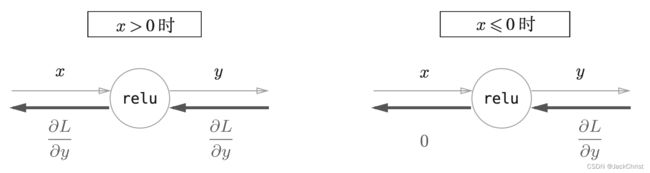
Relu层

$$y=\{\begin{array}{c}x(x>0)\\ 0(x\le 0)\end{array}$$
$$\frac{\partial y}{\partial x}=\{\begin{array}{c}1(x>0)\\ 0(x\le 0)\end{array}$$

Sigmoid层

$$y=\frac{1}{1+exp(-x)}$$
用计算图表达这个式子，如图所示（事实上这么一个式子，并不是只有一种固定的计算图表示）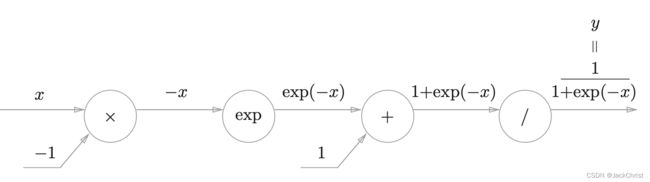
经过一定的运算，可以得到下图的答案。

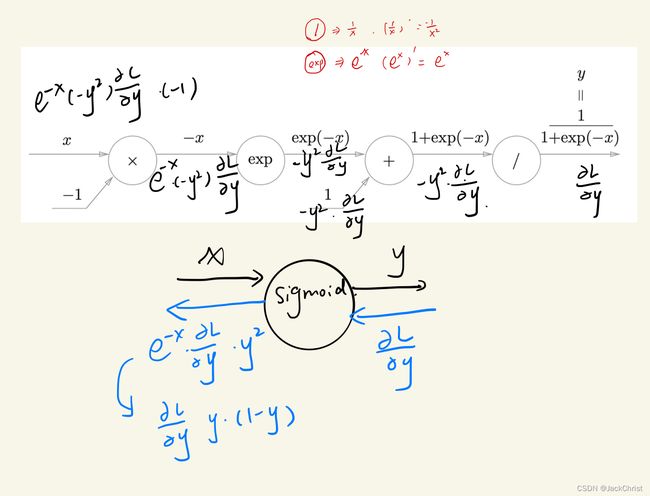
当然，不需要记住任何反向传播的公式，仅仅是知道他的流程即可。目前来讲我们了解了两种求梯度的方法，一种是基于数值解的，一种是基于解析解的，很明显误差反向传播法属于基于解析解的。
通过误差反向传播法，就可以知道神经网络中每一步的优化，从而使loss不断地下降。
举例来讲，上图输入x，输出y。那么怎么调整x，已经算出来了$x=x-\frac{\partial L}{\partial y}y(1-y)$。
之后x就更新了，随着x的更新y也更新了，就这样一直循环下去就可以找到使sigmoid最低的x。

至此我们终于明白了，深度学习的目的就是为了使loss下降或上升，而误差反向传播可以通过调整x来完成这个任务。¹

---

1. 深度学习入门：基于python的理论与实现 ↩︎