【西瓜书】4-决策树
文章目录
-
- 4.1-基本流程
- 4.2-划分
-
- 4.2.1-信息增益(ID3)
- 4.2.2-信息增益率(C.45)
- 4.2.3-基尼指数(CART)
- 4.3-剪枝处理
- 4.4-连续与缺失值
-
- 4.4.2-连续值处理
- 4.4.1-缺失值处理
- 4.5-多变量决策树
- 碎碎念
4.1-基本流程
决策树(DTs)是一种用于分类和回归的非参数有监督学习方法。
其目标是创建一个模型,通过学习从数据特性中推断出的简单决策规则来预测目标变量的值1。
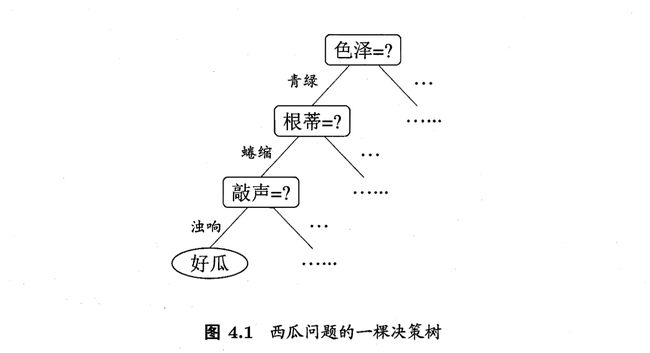
例如,在西瓜例子中,我们可以先观察西瓜颜色,然后在此条件下再次决策(子决策),直到能够判断出好瓜还是坏瓜。
这里给出决策树学习基本算法的伪代码
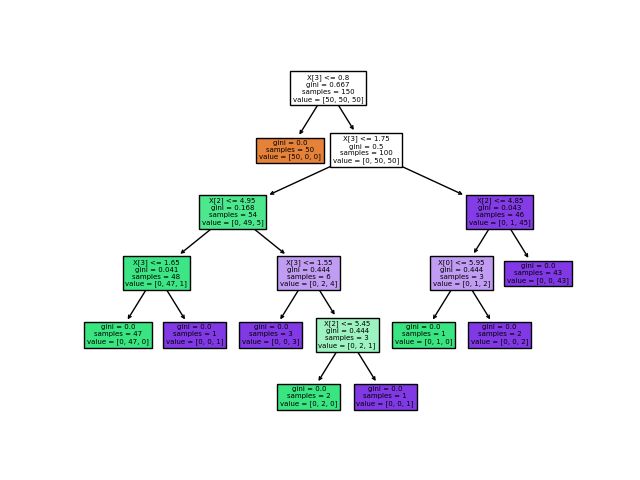
sklearn中的决策树api演示:
from sklearn.datasets import load_iris
from sklearn import tree
X, y = load_iris(return_X_y=True)
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X, y)
tree.plot_tree(clf)
4.2-划分
当我们的属性变得比较多,那么决策树就会变得很长,这时候需要的是一个高效的决策树,使得我们能够以尽量小的决策步骤将数据划分出来,或者说一次划分尽可能多的数据。
4.2.1-信息增益(ID3)
在信息论中,熵可以衡量随机变量的不确定性,上越大就表明信息越不明确。
信息的整体的熵:
Ent ( D ) = − ∑ k = 1 ∣ Y ∣ p k log 2 p k (4.1) \operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|} p_{k} \log _{2} p_{k} \tag{4.1} Ent(D)=−k=1∑∣Y∣pklog2pk(4.1)
假定离散属性 a a a 有 V V V 个取值,那么可以计算 a a a 取值为 v v v 时的熵2 D v D^v Dv, 考虑到样本数量的影响,最终得到信息增益
Gain ( D , a ) = Ent ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) (4.2) \operatorname{Gain}(D, a)=\operatorname{Ent}(D)-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right) \tag{4.2} Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)(4.2)
那么只需要递归地选取能使信息增益最大化的属性 a ∗ a_* a∗ 就行,即 a ∗ = arg max a ∈ A Gain ( D , a ) a_{*}=\underset{a \in A}{\arg \max } \operatorname{Gain}(D, a) a∗=a∈AargmaxGain(D,a)。这就是ID3算法
4.2.2-信息增益率(C.45)
C4.5决策树的提出完全是为了解决ID3决策树的一个缺点,当一个属性的可取值数目较多时,那么可能在这个属性对应的可取值下的样本只有一个或者是很少个,那么这个时候它的信息增益是非常高的,这个时候纯度很高,ID3决策树会认为这个属性很适合划分,但是较多取值的属性来进行划分带来的问题是它的泛化能力比较弱,不能够对新样本进行有效的预测。3
与ID3算法不同,C4.5算法使用信息增益率来划分决策树
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) (4.3) Gain\_ratio(D,a) = \frac{Gain(D,a)}{IV(a)} \tag{4.3} Gain_ratio(D,a)=IV(a)Gain(D,a)(4.3)
其中
I V ( a ) = ∑ v = 1 V ∣ D v ∣ D log 2 ∣ D v ∣ ∣ D ∣ (4.4) IV(a) = \sum_{v=1}^{V}{\frac{|D^v|}{D}\log_2{\frac{|D^v|}{|D|}}} \tag{4.4} IV(a)=v=1∑VD∣Dv∣log2∣D∣∣Dv∣(4.4)
但是增益率准则对可取值数目较少的属性有所偏好,于是C4.5会先算信息增益,找到大于平均值的然后选取其中增益率最高的划分。
4.2.3-基尼指数(CART)
CART决策树使用基尼指数划分
基尼值表示任意取两个样本,其不一致的概率:
G i n i ( D ) = ∑ k = 1 ∣ y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ y ∣ p k 2 (4.5) Gini(D) = \sum_{k=1}^{|y|}{\sum_{k^\prime\neq k}{p_kp_{k^\prime}}} = 1 - \sum_{k=1}^{|y|}{p_k^2} \tag{4.5} Gini(D)=k=1∑∣y∣k′=k∑pkpk′=1−k=1∑∣y∣pk2(4.5)
基尼指数:
G i n i _ i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ D G i n i ( D v ) Gini\_index(D,a) = \sum_{v=1}^{V}{\frac{|D^v|}{D}Gini(D^v)} Gini_index(D,a)=v=1∑VD∣Dv∣Gini(Dv)
4.3-剪枝处理
剪枝处理是避免模型过拟合的常用手段,常见的有预剪枝和后剪枝。
预剪枝:决策树生成过程中,在划分前估计,如果不能提升泛化能力,那么停止
后剪枝:决策树生成后,自底向上,将不能提示泛化能力的叶子节点剪掉
4.4-连续与缺失值
4.4.2-连续值处理
当属性的取值不再离散时,我们需要做什么?连续值离散化
最简单的策略:二分法(bi-partition),对于数学 a a a 的取值,按照数值划分成大于和小于的两种,这里取排序后相邻取值的中位数作为划分边界。
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } (4.7) T_a = \left\{\frac{a_i+a_{i+1}}{2}\ | \ 1 \leq i \leq n-1 \right\}\tag{4.7} Ta={2ai+ai+1 ∣ 1≤i≤n−1}(4.7)
Gain ( D , a ) = max t ∈ T a Gain ( D , a , t ) = max t ∈ T a Ent ( D ) − ∑ λ ∈ { − , + } ∣ D t λ ∣ ∣ D ∣ Ent ( D t λ ) (4.8) \begin{aligned} \operatorname{Gain}(D, a) &=\max _{t \in T_{a}} \operatorname{Gain}(D, a, t) \\ &=\max _{t \in T_{a}} \operatorname{Ent}(D)-\sum_{\lambda \in\{-,+\}} \frac{\left|D_{t}^{\lambda}\right|}{|D|} \operatorname{Ent}\left(D_{t}^{\lambda}\right) \end{aligned} \tag{4.8} Gain(D,a)=t∈TamaxGain(D,a,t)=t∈TamaxEnt(D)−λ∈{−,+}∑∣D∣∣∣Dtλ∣∣Ent(Dtλ)(4.8)
4.4.1-缺失值处理
数据中常有缺失值,如果直接丢弃,那么数据集的浪费将是指数级的。
这时我们面临两个问题:
(1) 如何在属性值缺失的情况进行划分属性选择?
- 去掉该属性缺失的属性值对应的样本
- 计算信息增益
- 用无缺失值的样本所占比例乘以去除缺失值的属性的信息增益
Gain ( D , a ) = ρ × Gain ( D ~ , a ) = ρ × ( Ent ( D ~ ) − ∑ v = 1 V r ~ v Ent ( D ~ v ) ) (4.12) \begin{aligned} \operatorname{Gain}(D, a) &=\rho \times \operatorname{Gain}(\tilde{D}, a) \\ &=\rho \times\left(\operatorname{Ent}(\tilde{D})-\sum_{v=1}^{V} \tilde{r}_{v} \operatorname{Ent}\left(\tilde{D}^{v}\right)\right) \end{aligned} \tag{4.12} Gain(D,a)=ρ×Gain(D~,a)=ρ×(Ent(D~)−v=1∑Vr~vEnt(D~v))(4.12)
(2) 给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?
- 将该样本放到所有的分支中,并赋以不同的权重,权重为各分支的样本数占排除该属性值为缺失的样本总数比例。
- 相当于让同一个样本以不同的概率划入到不同的子结点中去.
4.5-多变量决策树
假设你在西瓜数据集上训练出了一下决策树

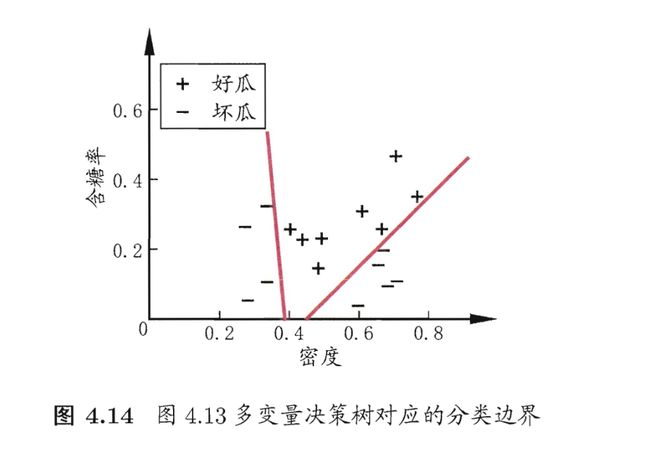
其分类边界如下图所示
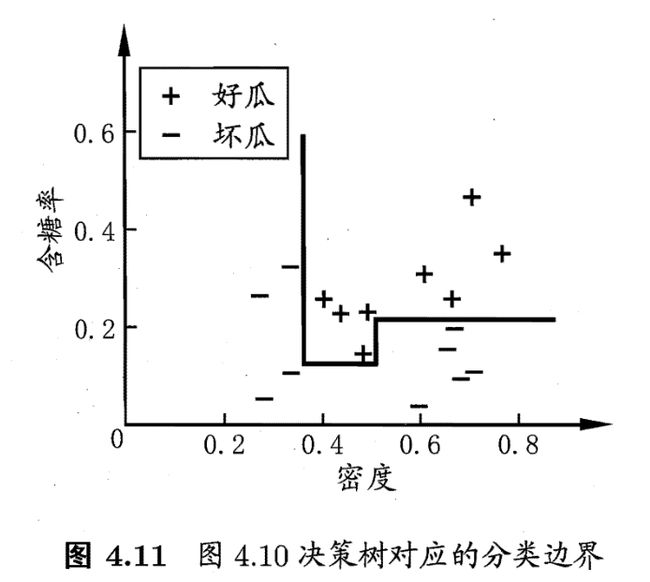
仔细观察会发现有几道弯,是否有办法简化一下决策树呢?
其实可以组合 含糖率 与 密度,构造一个新属性
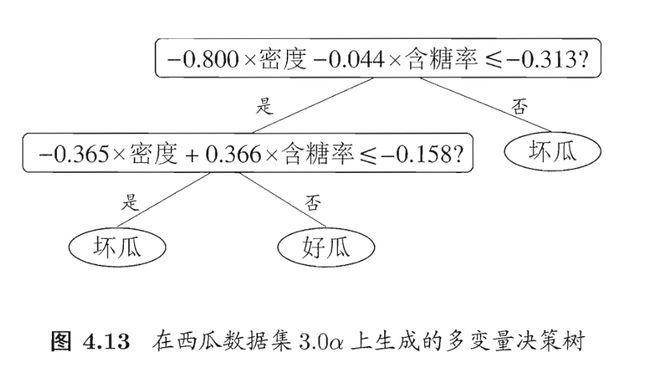
以上图为例,其构造了两个新属性:
- − 0.8 ∗ 密度 − 0.044 × 含糖率 ≤ − 0.313 -0.8 * \text{密度} - 0.044 \times \text{含糖率} \leq -0.313 −0.8∗密度−0.044×含糖率≤−0.313
- − 0.365 × 密度 + 0.366 × 含 糖 率 ≤ − 0.158 -0.365 \times \text{密度}+0.366\times{含糖率}\leq -0.158 −0.365×密度+0.366×含糖率≤−0.158
碎碎念
- GitHub笔记地址:https://github.com/hyperv0id/cs-notes/blob/main/ai/watermelon/4-%E5%86%B3%E7%AD%96%E6%A0%91.md
1.10 决策树-scikit-learn中文社区 ↩︎
这里不严谨,a的取值为 { a , a 1 , a 2 , … , a V } \{a,a^1,a^2,\dots,a^V\} {a,a1,a2,…,aV} ↩︎
ID3、C4.5、CART三种决策树的区别_夏末的初雪的博客-CSDN博客 ↩︎