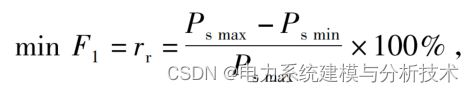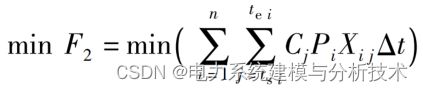基于精英遗传算法的电动汽车有序充电策略

目录

摘要：

1.电动车无序充电特性：

2.电动车有序充电模型：

2.1 峰谷差最小

2.2 充电费用最小

3.精英遗传算法：

4.有序充放电调度结果：

5.Matlab程序实现：

---

摘要：

为了减小电动汽车规模化充电给配电网安全稳定运行带来的不利影响，提出一种基于精英遗传算法的电动汽车有序充电策略。考虑用户出行规律及保证配电网的安全稳定运行，以降低负荷曲线峰谷差与充电成本最小为目标，建立峰值不超过变压器容量和电池电量充满为约束的优化模型。采用精英遗传算法对该问题进行求解，所得结果表明有序充电相比于无序充电，能有效降低配电网的峰谷差同时节约电动车充电的成本。本文基于Matlab平台编程实现，有相关参考文献，代码注释详细、可修改性强，适合初学者模仿学习。

1.电动车无序充电特性：

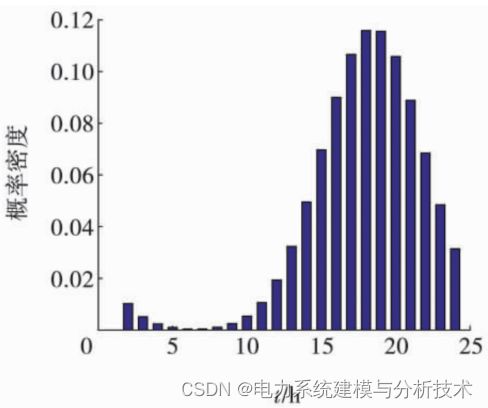
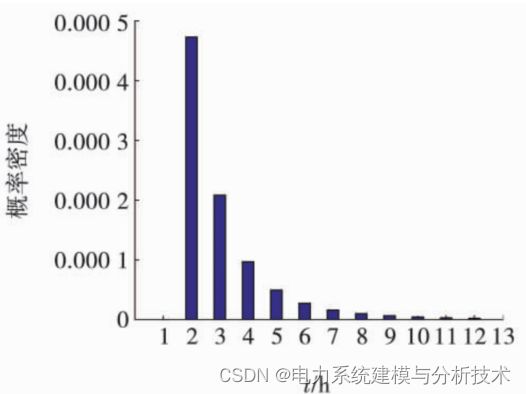
无序充电是指用户无任何约束而给电动汽车充电的行为。根据 2009 年美国 NHTS 统计结果显示，来分析电动汽车开始充电时间、日行驶里程、充电时间等相关参数，可以绘制如下的电动车无序充电特性图：

左图为用户返程时间概率密度分布，右图为用户出行时间概率密度分布

可以发现大多数用户都是选择下班回到家就开始充电而早上出门后一般不会充电，这就会导致某一时刻大量用户聚集充电。规模化电动汽车充电会引起电网负荷激增而导致基础负荷峰上加峰现象。

2.电动车有序充电模型：

2.1 峰谷差最小

集聚充电时负荷曲线上就会表现出峰值和谷底相差较大，影响电网平衡而且造成资源利用不合理。以负荷峰谷差率最小建立目标函数为

其中：

2.2 充电费用最小

设置分时充电价格，用户如果考虑充电成本则会有部分用户选择在电价低的低谷时间段充电，从而减小负荷峰值减轻电网压力，以充电成本最小的目标函数为

3.精英遗传算法：

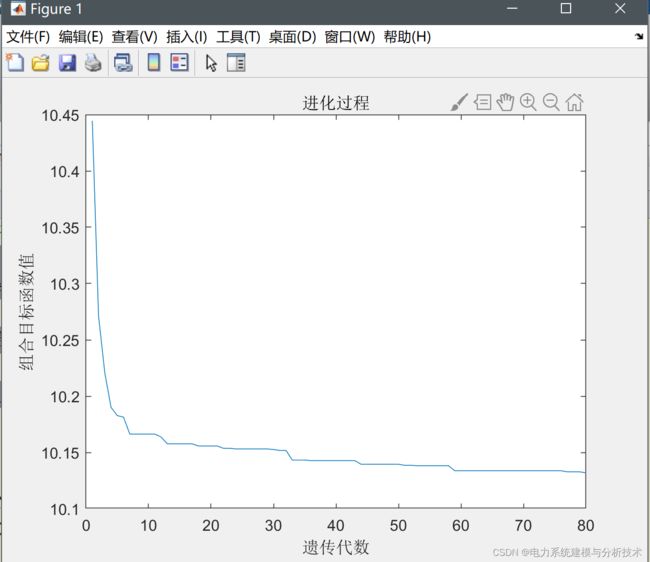
本文建立了基于精英遗传算法( ESGA) 求解模型，相比于普遍使用的基于轮盘赌选择的传统遗传算法具有更快的收敛速度。ESGA 的基本思想: 依据上一代种群的适应度建立精英种群，在新一代的选择的过程中，用精英种群替换种群中适应度低的个体。为了保证算法不过早限于局部最优，在遗传过程中适当修改交叉和变异率，k 为迭代次数，kk 为达到最优解连续不变的代数，M 为最优解保持连续不变的最大迭代次数，也就是说一旦迭代过程中最优解保持不变达到 M 代就对变异率和交叉率进行修改。ESGA 流程如图 4 所示。

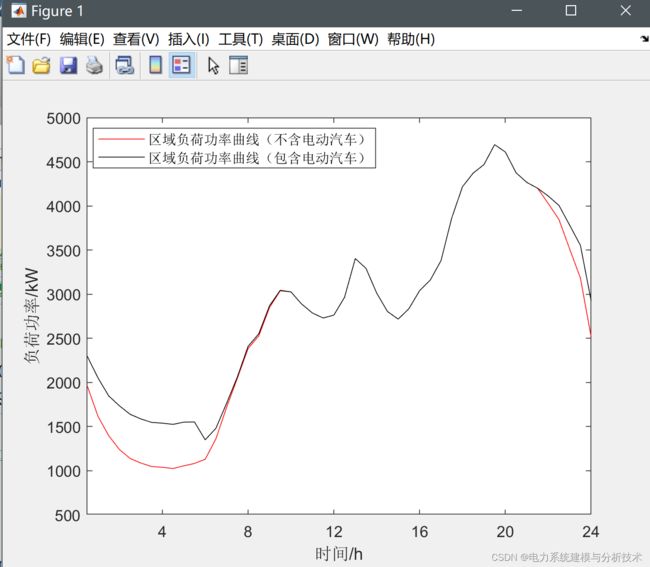
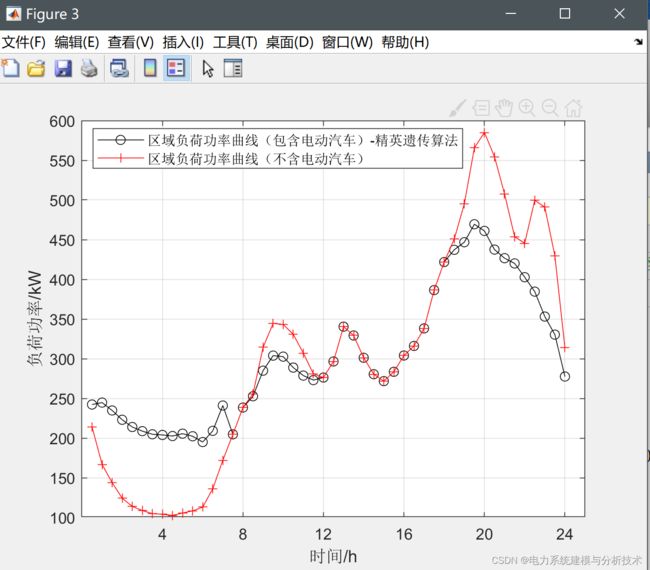
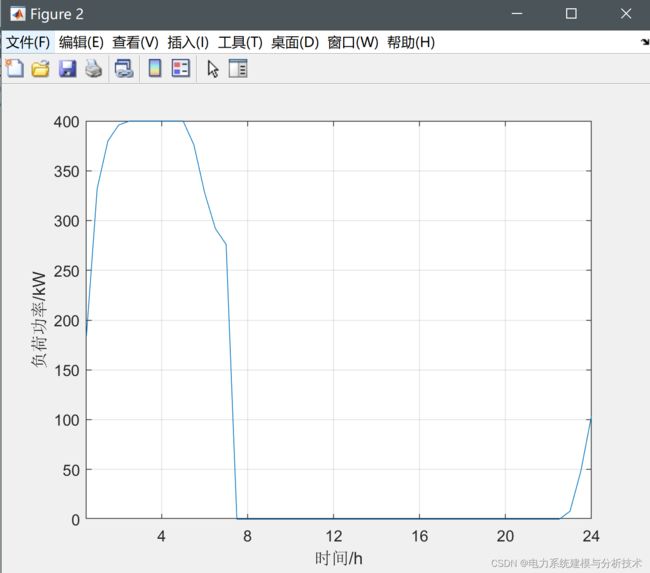
4.有序充放电调度结果：

5.Matlab程序实现：

本文仅展示部分代码，完整版的代码及相关数据在：正在为您运送作品详情

%% 主函数
clc
clear
warning off
%实时电价数据导入，数据来源PJM
RP=[3.10000000000000,3.05000000000000,3,2.80000000000000,2.60000000000000,2.55000000000000,2.50000000000000,2.60000000000000,2.70000000000000,2.80000000000000,2.90000000000000,3.20000000000000,3.50000000000000,3.60000000000000,3.70000000000000,3.67500000000000,3.65000000000000,3.70000000000000,3.75000000000000,3.82500000000000,3.90000000000000,3.92500000000000,3.95000000000000,4.02500000000000,4.10000000000000,4.15000000000000,4.20000000000000,4.20500000000000,4.21000000000000,4.28000000000000,4.35000000000000,4.42500000000000,4.50000000000000,4.60000000000000,4.70000000000000,4.62000000000000,4.54000000000000,4.39500000000000,4.25000000000000,4.22500000000000,4.20000000000000,4.05000000000000,3.90000000000000,3.60000000000000,3.30000000000000,3.20000000000000,3.10000000000000,3.10000000000000];
Price=[RP(35:48),RP(1:14)];% 设定车辆每天17:00之后才回家充电；每天7点之后就离家不充电
Num=100;%电动车数量
PEV=4;
global PEV
load EV_WX
% load SOC_start
SOC_start=normrnd(0.3,0.05,1,Num);
global SOC_start
SOC_end=0.95*ones(1,Num);
global SOC_end
C=35; 
global C
number=Num;%种群中个体数量
%% 遗传算法参数设定
NP=300;% 产生初始种群的总数
NG=80 ;% 迭代的 总次数
Pc=0.8;  
Pm=0.4;% 变异率
COUNTER=10;
%% 产生初始种群
for i=1:NP
    data(i).Initial=Initial(number);
    data(i).generation=data(i).Initial;
end
%% 计算初始种群适应度
for i=1:NP
    data(i).Fitness=Fitness(data(i).generation,PEV,Price,SOC_start,SOC_end,C);
end
intinial_Fitness_1=max([data(:).Fitness]);
%% 进行遗传，交叉，变异
maxium_Fitness=[];
temp_Fitness=intinial_Fitness_1;