使用MLP和CNN实现MNIST手写数字识别
使用MLP和CNN实现MNIST手写数字识别
- MNIST手写数据集的介绍
- 环境介绍
- MLP多层感知机(原始神经网络)
-
- 代码部分
- CNN实现数字手写识别
-
- 代码部分
MNIST手写数据集的介绍
MNIST 数据集来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员.
训练数据集包含 60,000 个样本, 测试数据集包含 10,000 样本. 在 MNIST 数据集中的每张图片由 28 x 28 个像素点构成, 每个像素点用一个灰度值表示. 在这里, 我们将 28 x 28 的像素展开为一个一维的行向量, 这些行向量就是图片数组里的行,每行 784 个值, 或者说每行就是代表了一张图片(摘录自博客园)
环境介绍
Win10
PyCharm
Anaconda
Python3.6
Tensorflow 1.10
Keras 2.2.0
(tensorflow和keras需要版本对应,如不使用这两个版本可使用其他的,可见tensorflow和keras版本对应关系.)
MLP多层感知机(原始神经网络)
MLP多层感知机,即原始神经网络。只用全连接层,没有卷积层,只接受向量(一维数组)作为输入,不接受矩阵(二维数组),丢失图像中的像素关系
代码部分
创建虚拟模型:3层全连接层与2层随机失活层交替进行,最后一层全连接层因为是1~10即10分类所以最终全连接层参数为10,'softmax’为激活函数,专门针对多分类。自己设计的时候可以尝试其他的全连接层的参数,选取准确率高且收敛速度快的参数。
model = Sequential()
model.add(Dense(512,activation='relu',input_shape=(784,))) #全连接层,激活函数,输入784个向量
model.add(Dropout(0.2)) #随机失活层,为了不过拟合
model.add(Dense(512,activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(10,activation='softmax'))
model.summary() #把每一层都打印出来
训练模型:这里涉及到迭代次数与一次训练所选取样本数的关系,batch Size是一次训练所选取的样本数。batch Size的大小影响模型的优化程度和速度。同时其直接影响到GPU内存的使用情况,假如GPU内存不大,该数值最好设置小一点。Batch Size增大了,要到达相同的准确度,必须要增大epoch(迭代次数)。 具体可看这篇博客神经网络中Batch Size的理解.
model.fit(x_train,y_train,
batch_size = 128,
epochs = 10,
verbose=1, #每迭代一次打印一条记录在控制台上
validation_data=(x_test,y_test)) #指定验证集
完整代码:
在每行代码后基本都有注释,想深究其理的朋友可以把代码复制问百度。
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense,Dropout
from keras.optimizers import RMSprop
import matplotlib.pyplot as plt
batch_size = 128 #一般是2的n次方
epochs = 10 #迭代次数
num_classes =10 #输出十类1~10
(x_train,y_train),(x_test,y_test) = mnist.load_data() #直接通过keras在网上下载mnist的数据集
x_train = x_train.reshape(60000,784) #训练数据60000个,784个像素点
x_test = x_test.reshape(10000,784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /=255
x_test /=255 #归一化,加快模型收敛,提高模型精确度
print(x_train.shape[0],'train samples')
print(x_test.shape[0],'train samples')
# one-hot
y_train = keras.utils.to_categorical(y_train)
y_test = keras.utils.to_categorical(y_test) #将数字图片表示的标签转化为one-hot代码
#创建虚拟模型
model = Sequential()
model.add(Dense(512,activation='relu',input_shape=(784,))) #全连接层,激活函数,输入784个向量
model.add(Dropout(0.2)) #随机失活层,为了不过拟合
model.add(Dense(512,activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(num_classes,activation='softmax')) #最后一层全连接,10分类,10个神经元,'softmax'为激活函数,专门针对多分类
model.summary() #把每一层都打印出来
#编译模型
model.compile(loss='categorical_crossentropy', #损失函数,多分类交叉熵
optimizer=RMSprop(), #优化器
metrics=['accuracy']) #评价指标(精确度)
#训练模型
model.fit(x_train,y_train,
batch_size = batch_size,
epochs = epochs,
verbose=1, #每迭代一次打印一条记录在控制台上
validation_data=(x_test,y_test)) #指定验证集
#观察验证集的前十个图片
n = 10
predicted_number = model.predict(x_test[:n],n) #预测验证集里面的前十个图像
plt.figure(figsize=(10,2)) #宽十英寸,高2英寸
for i in range(n):
plt.subplot(1,10,i + 1)
t = x_test[i].reshape(28,28)
plt.imshow(t, cmap='gray')
plt.subplots_adjust(wspace=2)
if y_test[i].argmax() == predicted_number[i].argmax(): #如果预测的标签可以等于真实的标签,color= 'green'
plt.title(str(y_test[i].argmax()) + "," + str(predicted_number[i].argmax()),color= 'green')
else:
plt.title(str(y_test[i].argmax()) + "," + str(predicted_number[i].argmax()), color='red')
plt.xticks([])
plt.yticks([])
plt.show()
CNN实现数字手写识别
CNN又称卷积神经网络,网上解释的过程很复杂,可以这样简单的理解:
训练集的图片有图像和对应的标签,将图片的每个像素点的灰度值放入到神经网络之后会以标签的值作为标准通过损失函数进行学习(调整权重参数,也就是训练)。训练完成后输入测试图片通过卷积层进行特征提取,最后的全连接层进行特征匹配,输出匹配最高的,即为测试图片所代表的值。与MLP不同的是使用了卷积层,可接受矩阵作为输入。
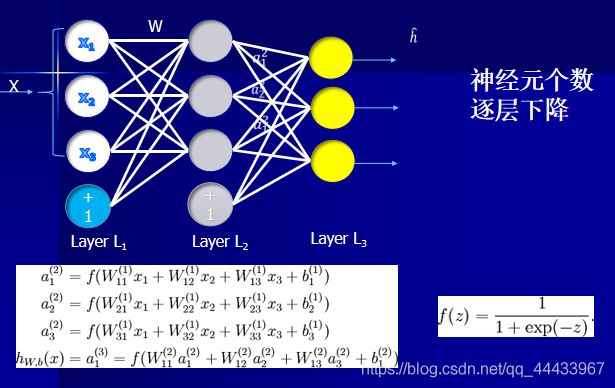
上图为CNN网络权重参数
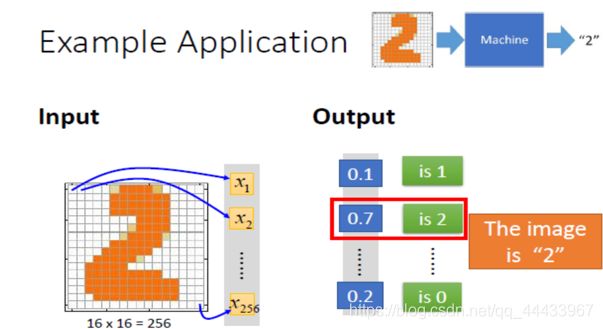 上图为16x16输入测试图片,输出"2"
上图为16x16输入测试图片,输出"2"
代码部分
创建虚拟模型:两个卷积层一个池化层,最后Flatten函数将矩阵展开抻直,为进入全连接层做准备,CNN与MLP的不同在于多了卷积层和池化层,在进行较大数据集的学习时往往能够更快的收敛。自己设计的时候同样可以尝试改变卷积层的参数,选取准确率高且收敛速度快的参数。
model = Sequential()
model.add(Conv2D(32,kernel_size=(3,3), #32个卷积核
activation='relu',
input_shape = input_shape))
model.add(Conv2D(64,(3,3), #64个卷积核
activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2))) #池化
model.add(Dropout(0.2)) #随机失活层,为了不 过拟合
model.add(Flatten()) #将矩阵展开抻直
model.add(Dense(128,activation='relu')) #全连接层,激活函数
model.add(Dropout(0.5))
model.add(Dense(10,activation='softmax')) #最后一层全连接,10分类,10个神经元,activation='softmax'为激活函数
model.summary()
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy']) # 评价指标(精确度)
训练模型:这里我训练了10轮,大概用了15分钟,准确率为99.14% ,也可以采用更高的轮数求得更高准确率。
model.fit(x_train,y_train,
batch_size = 128,
epochs = 10,
verbose=1, #每迭代一次打印一条记录在控制台上
validation_data=(x_test,y_test)) #指定验证集观察是否过拟合
完整代码:
import keras
from keras import Sequential
from keras.datasets import mnist
from keras.layers import Conv2D,MaxPooling2D,Dropout,Flatten,Dense
import matplotlib.pyplot as plt
batch_size = 128
epochs = 10
num_classes =10
img_rows, img_cols=28,28
(x_train,y_train),(x_test,y_test) = mnist.load_data() #直接通过keras在网上下载mnist的数据集
#(n_samples,rows,cols,channels)CNN里面的x都是四维张量
x_train=x_train.reshape(x_train.shape[0],img_rows, img_cols,1) #把x_train转化成四维张量然后再输入
x_test=x_test.reshape(x_test.shape[0],img_rows, img_cols,1)
input_shape = (img_rows, img_cols,1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /=255
x_test /=255
print(x_train.shape[0],'train samples')
print(x_test.shape[0],'train samples') #看训练样本和测试样本各有多少个
# one-hot
y_train = keras.utils.to_categorical(y_train,num_classes)
y_test = keras.utils.to_categorical(y_test,num_classes) #将数字图片表示的标签转化为one-hot代码
#创建虚拟模型
model = Sequential()
model.add(Conv2D(32,kernel_size=(3,3), #32个卷积核
activation='relu',#每个卷积层后加RELU激活函数
input_shape = input_shape))
model.add(Conv2D(64,(3,3), #64个卷积核
activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2))) #池化
model.add(Dropout(0.2)) #随机失活层,为了不 过拟合
model.add(Flatten()) #将矩阵展开抻直
model.add(Dense(128,activation='relu')) #全连接层,激活函数
model.add(Dropout(0.5))
model.add(Dense(num_classes,activation='softmax')) #最后一层全连接,10分类,10个神经元,activation='softmax'为激活函数
model.summary()
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy']) # 评价指标(精确度)
model.fit(x_train,y_train, #训练模型
batch_size = batch_size,
epochs = epochs,
verbose=1, #每迭代一次打印一条记录在控制台上
validation_data=(x_test,y_test)) #指定验证集观察是否过拟合
n = 10
predicted_number = model.predict(x_test[:n],n) #预测验证集里面的前十个图像
plt.figure(figsize=(10,2)) #宽十英寸,高二英寸
for i in range(n):
plt.subplot(1,10,i + 1) #用来描述子图的位置信息
t = x_test[i].reshape(28,28)
plt.imshow(x_test[i], cmap='gray')
plt.subplots_adjust(wspace=2) #如果预测的标签可以等于真实的值
if y_test[i].argmax() == predicted_number[i].argmax():
plt.title(str(y_test[i].argmax()) + "," + str(predicted_number[i].argmax()),color= 'green')
else:
plt.title(str(y_test[i].argmax()) + "," + str(predicted_number[i].argmax()), color='red')
plt.xticks([])
plt.yticks([])
plt.show()

