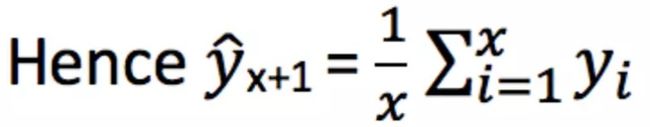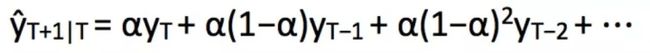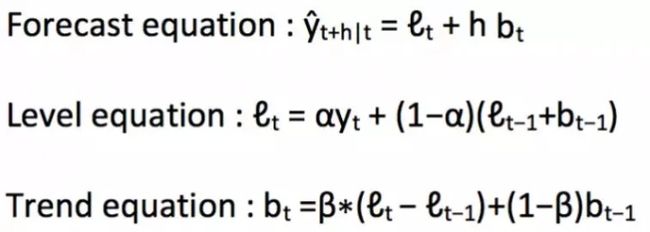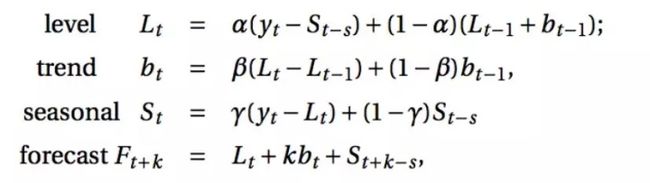时间序列预测模型_基于时间序列模型预测之七种武器

前言

在许多重要的领域，需要基于时间序列进行预测，例如：预测销售量，呼叫中心的通话量，太阳能活动，海潮，股市行为等等。

假设酒店经理想预测明年会有多少游客，来以此调整酒店的库存，合理地猜测酒店的收入。根据过去某年/月/日的数据，他可以使用时间序列预测，得到访问者的大致值。游客的预测值将有助于酒店管理资源，并据此规划计划。

在本文中，我们将学习多种预测技术，并通过在数据集上对它们进行比较。我们将通过不同的技巧，看看如何使用这些方法来提高预测分数。

问题陈述和数据集

场景：一家位于山上的酒店，酒店的访问量随着时间总体是持续增长的，它在夏季期间有很高的访问量，而一年内余下时间的游客相对较少，每逢周末的访问量也会比工作日多。

数据集样本

头部

id dt Count

0 0 2012-01-01 00:00 1.0000

1 1 2012-01-01 01:00 1.0001

2 2 2012-01-01 02:00 1.0004

3 3 2012-01-01 03:00 1.0009

4 4 2012-01-01 04:00 1.0016

数据样本尾部

id dt Count

11851 11851 2013-05-08 19:00 2790.127098

11852 11852 2013-05-08 20:00 3298.490395

11853 11853 2013-05-08 21:00 1600.653698

11854 11854 2013-05-08 22:00 1864.217009

11855 11855 2013-05-08 23:00 2416.380327

数据样本图例

蓝色：代表历史数据。

黄色：代表测试数据，用来和预测结果做对比。

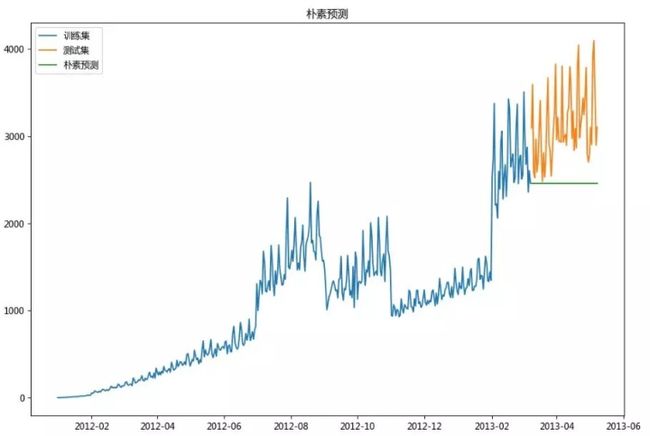
武器一：朴素法

“ 一个人只要懂得利用自己的长处，根本不必用武功也一样能够将人击倒。 ” ——《长生剑》

naive RMSE= 778.6931725867004

从上图和 RMSE 值可以看到，朴素法不适合高变异数据集，它最适合稳定的数据集。我们可以通过采用不同的技术来提高分数，现在我们来看看另一种技术，努力提高我们的得分。

武器二： 简单平均法

“ 真正的胜利，并不是你用武器争取的，那一定要用你的信心。无论多可怕的武器，也比不上人的信心。 ” ——《孔雀翎》

simple_avg RMSE= 2127.4877858798422

我们可以看出这个模型没有提高我们的成绩（事实上误差更大了）。

因此，我们可以从得分推断，这种方法在每次平均保持不变时效果最好。虽然朴素法的得分优于均值法，但这并不意味着朴素方法在所有数据集上都优于平均法。我们应该一步一步地尝试每个模型，并确认它是否改进了我们的模型。

武器三： 移动平均法

“ 要在茫茫的人海中，找到她这么样一个人，岂非也正如想从湖水中捞起那柄碧玉刀一样 ?” ——《碧玉刀》

moving_avg RMSE= 1034.080985549067

我们可以看到，在这个数据集上，朴素法优于平均法和移动平均法。

下面我们来看一下简单指数平滑法，看看它是如何执行的。

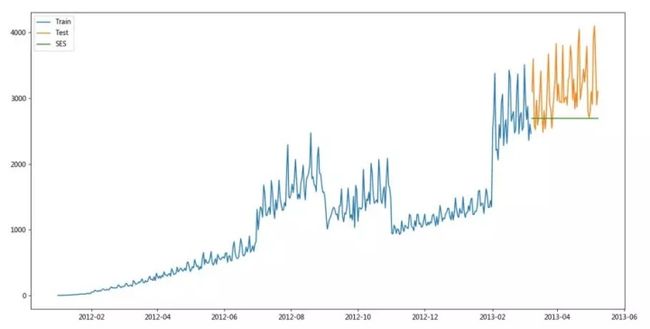
武器四：简单指数平滑法

“ 离别是为了相聚，只要能相聚，无论多痛苦的离别都可以忍受。 ” ——《离别钩》

ses RMSE= 595.6207801874045

可以看到，截至目前为止，简单指数平滑法取得了最佳得分，简单指数平滑法关键在于调参，合适的参数可以获得更理想的结果。

至于怎么确定最优参数，目前看就是针对测试数据集反复尝试，数据不一样，参数随之而变。

武器五：霍尔特线性趋势法

“ 现在我才知道，无论多高深的武功，也比不上真正的友情。 ” ——《拳头》

holt_linear RMSE= 419.109233039215

从所得图表可以看出，该数据集呈增长趋势。因此，我们可以用 Holt 的线性趋势来预测未来的数值。

Holt 扩展了简单指数平滑，允许有趋势的数据预测。它只适用于两个 Level（级数中的平均值）和趋势的指数平滑。

我们在上述算法中预测的值称为 Level。在上面的三个等式中，你可以注意到我们增加了 Level 和趋势来生成预测方程。

体会：霍尔特线性趋势法对于参数的调整影响更敏感，不同的参数组合可能会输出截然相反的趋势预测，这个方法已经可以用于对精度要求不是那么高的预测了。

武器六：霍尔特-温特斯法

“ 一个人只要有勇气去冒险，天下就绝没有不能解决的事。 ” ——《霸王枪》

我们在这个算法引入一个新术语 Holt-Winters。

从数据得出，酒店的利润在夏季比其他季节都要好得多，这种模式每年都会重演，即季节性，数据集在一段时间固定的间隔内显示出相似的模式。

上述模型没有考虑到数据集的季节性，因此，我们需要一种既考虑趋势又考虑季节性的方法来预测。

Holt-Winters 季节性方法包括预测方程和三个平滑方程：一个水平 ℓT，一个趋势 BT 和一个季节 ST，平滑参数 α，β 和 γ。

其中 S 是季节性周期的长度，0≤α≤1, 0≤β≤1 和 0≤γ≤1。

水平方程在季节性调整后的观测值与非季节性的时间 t 之间有一个加权平均值，趋势方程与 Holt 线性方法相同。

季节性方程显示了当前季节性指数和去年同一季节的季节指数之间的加权平均值（即 S 时间段）。

在该方法中，我们还可以同时使用加法和乘法。当季节变化大致为常数时，加法是首选的，而当季节变化与级数水平成比例时，乘法是首选的。

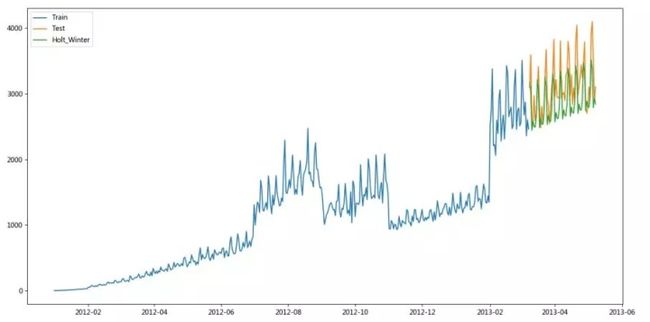
holt_winters RMSE= 361.4077596555284

从图表可以看出：Holt-Winters 法很好的预测了周期性变化的影响，同时也在趋势上与测试数据保持了一致。

武器七：ARIMA（综合自回归移动平均法）

“ 自东方照射过来的第一线阳光，也就在这一瞬间，刚好照在这件武器上，使得它忽然闪起一种又玄妙又邪恶的光采。 ” ——《英雄无泪》

另一个在数据科学家中非常流行的时间序列模型是 ARIMA。

指数平滑模型是基于对趋势和季节性数据的描述，ARIMA 模型的目的是描述数据之间的相关性。

ARIMA 的改进模型是季节性 ARIMA，它考虑了数据集的季节性，就像 Holt-Winters 方法一样。

arima RMSE= 290.28251785239894

可以看出：ARIMA 法和 Holt-Winters 法预测的结果相近，在这个数据集上的得分甚至更好。

结论

希望这篇文章可以帮你解决类似的时间序列问题，试试这些武器（模型），打造一件合身的套装，找出最适合于你的时间序列数据模型。

从以上步骤中可以学到的一点：每个模型在特定的数据集上才会优于其他模型。

欢迎关注公众号：数猎天下DataHunter－数据分析展示就用 DataHunter－

数据可视化大屏展示工具-免费试用​www.datahunter.cn?channel=weibo