为什么数据增强能防止过拟合:以曲线拟合为例
文章目录
- 本文档暂未完成
- 多项式+最小二乘法做曲线拟合的数学基础
- 程序
- 解释
-
- 训练和测试数据
- 使用原始训练数据做曲线拟合
- 过拟合现象的loss表现
- 数据增强
- 使用增强后的数据做曲线拟合
- 数据增强后的loss表现
本文档暂未完成
多项式+最小二乘法做曲线拟合的数学基础
记n次多项式的表达式为:
y = a 0 + a 1 x 1 + a 2 x 2 + . . . + a n x n y = a_0 + a_1x^1 + a_2x^2 + ... + a_nx^n y=a0+a1x1+a2x2+...+anxn
拟合的目的就是利用已知点求取所有的系数 a i a_i ai。
假设我们有m个点用来做拟合,m个点的坐标为: ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) (x_1, y_1), (x_2, y_2), ... , (x_m, y_m) (x1,y1),(x2,y2),...,(xm,ym)
上述点的坐标均为已知内容,将其代入多项式可得:
a 0 + a 1 x 1 + a 2 x 1 2 + . . . + a n x 1 n = y 1 a 0 + a 1 x 2 + a 2 x 2 2 + . . . + a n x 2 n = y 2 . . . a 0 + a 1 x m + a 2 x m 2 + . . . + a n x m n = y m a_0 + a_1{x_1} + a_2{x_1}^2 + ... + a_n{x_1}^n = y_1 \\[2ex] a_0 + a_1{x_2} + a_2{x_2}^2 + ... + a_n{x_2}^n = y_2 \\[2ex] ... \\[2ex] a_0 + a_1{x_m} + a_2{x_m}^2 + ... + a_n{x_m}^n = y_m a0+a1x1+a2x12+...+anx1n=y1a0+a1x2+a2x22+...+anx2n=y2...a0+a1xm+a2xm2+...+anxmn=ym
将上述方程组写为线性方程形式:
[ 1 x 1 1 x 1 2 . . . x 1 n 1 x 2 1 x 2 2 . . . x 2 n . . . 1 x m 1 x m 2 . . . x m n ] [ a 0 a 1 . . . a n ] = [ y 1 y 2 . . . y m ] \begin{bmatrix} 1 & {x_1}^1 & {x_1}^2 & ... & {x_1}^n \\ 1 & {x_2}^1 & {x_2}^2 & ... & {x_2}^n \\ && ... \\ 1 & {x_m}^1 & {x_m}^2 & ... & {x_m}^n \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ ... \\ a_n \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ ... \\ y_m \end{bmatrix} ⎣⎢⎢⎡111x11x21xm1x12x22...xm2.........x1nx2nxmn⎦⎥⎥⎤⎣⎢⎢⎡a0a1...an⎦⎥⎥⎤=⎣⎢⎢⎡y1y2...ym⎦⎥⎥⎤
记:
X = [ 1 x 1 1 x 1 2 . . . x 1 n 1 x 2 1 x 2 2 . . . x 2 n . . . 1 x m 1 x m 2 . . . x m n ] X = \begin{bmatrix} 1 & {x_1}^1 & {x_1}^2 & ... & {x_1}^n \\ 1 & {x_2}^1 & {x_2}^2 & ... & {x_2}^n \\ && ... \\ 1 & {x_m}^1 & {x_m}^2 & ... & {x_m}^n \end{bmatrix} X=⎣⎢⎢⎡111x11x21xm1x12x22...xm2.........x1nx2nxmn⎦⎥⎥⎤
A = [ a 0 a 1 . . . a n ] A = \begin{bmatrix} a_0 \\ a_1 \\ ... \\ a_n \end{bmatrix} A=⎣⎢⎢⎡a0a1...an⎦⎥⎥⎤
Y = [ y 1 y 2 . . . y m ] Y = \begin{bmatrix} y_1 \\ y_2 \\ ... \\ y_m \end{bmatrix} Y=⎣⎢⎢⎡y1y2...ym⎦⎥⎥⎤
那么有如下推导:
X A = Y X T X A = X T Y ( X T X ) − 1 X T X A = ( X T X ) − 1 X T Y A = ( X T X ) − 1 X T Y XA=Y \\[2ex] X^TXA=X^TY \\[2ex] (X^TX)^{-1}X^TXA=(X^TX)^{-1}X^TY \\[2ex] A=(X^TX)^{-1}X^TY XA=YXTXA=XTY(XTX)−1XTXA=(XTX)−1XTYA=(XTX)−1XTY
最后的表达式就是A的最小二乘解,将求解出的A代入到多项式中,就可以得到多项式关于已知点的最小二乘拟合曲线。
注意,只有当 m > n m>n m>n 时,得到的是最小二乘意义下的解;当 m = n m=n m=n 时得到的是精确解,此时拟合曲线可以精准穿过所有的已知点;当 m < n m
程序
在代码中,将系数 a i a_i ai 称为模型 model,将待拟合的已知点称为训练集train data,将用来测试的点称为测试集test data。
代码中拟合是fit,fit的目的就是通过训练集求出模型(我们这里只是借用了训练的说法,实际上也没啥可训的,求解过程是一步到位。。。)。做预测是predict,predict的目的是针对任意输入,使用训练得到的模型求得输出。
代码构造了x_train, y_train, x_test, y_test用于测试,并根据这些数据画了一些图片以帮助理解。
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
DEGREE = [2, 4, 6, 8]
DEGREE_AUG = [2, 4, 6, 8, 10, 12]
class PolynomialModel(object):
def __init__(self, degree):
self.model = None
self.degree = degree
def _generate_x_matrix(self, X):
"""
generate X matrix
Parameters:
-----------
X: list or 1-dim numpy array
x coordinates of points
Returns:
--------
x_matrix: 2-dim numpy array
X matrix
"""
x_matrix = np.ones([len(X), self.degree + 1])
for i in range(1, self.degree + 1):
x_matrix[:, i] = np.power(X, i)
return x_matrix
def fit(self, X, Y):
"""
compute model by least square fitting
Parameters:
-----------
X, Y: list or 1-dim numpy array
coordinates of points (x, y)
"""
Y = np.array(Y)
x_mat = self._generate_x_matrix(X)
Y = np.reshape(Y, [Y.shape[0], 1])
self.model = np.linalg.inv(x_mat.T @ x_mat) @ x_mat.T @ Y
def predict(self, X):
"""
predict output of input X, using the computed model
Parameters:
-----------
X: list or 1-dim numpy array
x coordinates of points
"""
x_mat = self._generate_x_matrix(X)
Y = x_mat @ self.model
return Y
def compute_mse(y1, y2):
"""
compute mean square error
Parameters:
-----------
y1, y2: list or numpy array, with same shape
Returns:
--------
mse: mean square error
"""
y1 = np.array(y1)
y2 = np.array(y2)
assert np.product(y1.shape) == np.product(y2.shape)
y2 = np.reshape(y2, y1.shape)
mse = np.mean(np.power(y1 - y2, 2))
return mse
def gauss_augmentation(X, Y, aug_num, std):
"""
augment data using gauss distributed random number
Parameters:
-----------
X, Y: list or 1-dim numpy array
coordinates of points (x, y)
aug_num: augmentation number for each point
std: std of random number
Returns:
--------
x_aug, y_aug: augmented points
"""
assert len(X) == len(Y)
length = len(X)
x_aug = []
y_aug = []
for i in range(length):
x = X[i] + np.random.randn(aug_num) * std
y = Y[i] + np.random.randn(aug_num) * std
x_aug.append(x)
y_aug.append(y)
x_aug = np.array(x_aug).reshape([-1])
y_aug = np.array(y_aug).reshape([-1])
return x_aug, y_aug
def get_x_range(x, increment):
"""
get evenly distributed coordinates by input x, the low limit and high
limit of coordinates are min(x) and max(x), separately.
Parameters:
-----------
x: list or 1-dim numpy array
x coordinates of points
increment: float number
interval of adjacent coordinates
Returns:
--------
range: evenly distributed coordinates
"""
x = np.array(x)
xmin = np.min(x)
xmax = np.max(x) + increment
range = np.arange(xmin, xmax, increment)
return range
def plot_original_dataset(x_train, y_train, x_test, y_test):
plt.figure(1, figsize=(9, 6))
plt.plot(x_train, y_train,
color='red', marker='o', markersize=6,
linewidth=0, label='train_data')
plt.plot(x_test, y_test,
color='green', marker='o', markersize=6,
linewidth=0, label='test_data')
plt.legend()
plt.savefig('original_dataset.png')
def plot_augmented_dataset(x_train, y_train, x_test, y_test, x_aug, y_aug):
plt.figure(2, figsize=(9, 6))
plt.plot(x_train, y_train,
color='red', marker='o', markersize=6,
linewidth=0, label='train_data')
plt.plot(x_test, y_test,
color='green', marker='o', markersize=6,
linewidth=0, label='test_data')
plt.plot(x_aug, y_aug,
color='blue', marker='o', markersize=3,
linewidth=0, label='augmented_data')
plt.legend()
plt.savefig('augmented_dataset.png')
def plot_no_augmentation_model(x_train, y_train, x_test, y_test):
x_range = get_x_range(x_train, 0.1)
plt.figure(3, figsize=(15, 9))
for i, degree in enumerate(DEGREE):
plt.subplot(2, 2, i + 1)
poly_model = PolynomialModel(degree)
poly_model.fit(x_train, y_train)
y_predict = poly_model.predict(x_range)
plt.plot(x_train, y_train,
color='red', marker='o', markersize=6,
linewidth=0, label='train_data')
plt.plot(x_test, y_test,
color='green', marker='o', markersize=6,
linewidth=0, label='test_data')
plt.plot(x_range, y_predict, color='black', label='fitted curve')
plt.title('degree = %d' % degree)
plt.legend()
plt.savefig('no_augmentation_model.png')
def plot_loss_for_overfitting(x_train, y_train, x_test, y_test):
plt.figure(4, figsize=(9, 6))
degrees = get_x_range(DEGREE, 1)
train_loss = []
test_loss = []
for _, degree in enumerate(degrees):
poly_model = PolynomialModel(degree)
poly_model.fit(x_train, y_train)
train_predict = poly_model.predict(x_train)
test_predict = poly_model.predict(x_test)
train_mse = compute_mse(y_train, train_predict)
test_mse = compute_mse(y_test, test_predict)
train_loss.append(train_mse)
test_loss.append(test_mse)
plt.plot(degrees, train_loss, color='red', label='train_loss')
plt.plot(degrees, test_loss, color='green', label='test_loss')
plt.xlabel('degree')
plt.ylabel('mean square error')
plt.legend()
plt.savefig('loss_for_overfitting.png')
def plot_augmentation_model(x_train, y_train, x_aug, y_aug):
x_range = get_x_range(x_train, 0.1)
plt.figure(5, figsize=(15, 15))
for i, degree in enumerate(DEGREE_AUG):
plt.subplot(3, 2, i + 1)
poly_model = PolynomialModel(degree)
poly_model.fit(x_aug, y_aug)
y_predict = poly_model.predict(x_range)
plt.plot(x_train, y_train,
color='red', marker='o', markersize=6,
linewidth=0, label='train_data')
plt.plot(x_test, y_test,
color='green', marker='o', markersize=6,
linewidth=0, label='test_data')
plt.plot(x_range, y_predict, color='black', label='fitted curve')
plt.title('degree = %d' % degree)
plt.legend()
plt.savefig('augmentation_model.png')
def plot_loss_for_augmentation(x_train, y_train, x_test, y_test, x_aug, y_aug):
plt.figure(6, figsize=(9, 6))
degrees = get_x_range(DEGREE_AUG, 1)
train_loss = []
test_loss = []
for _, degree in enumerate(degrees):
poly_model = PolynomialModel(degree)
poly_model.fit(x_aug, y_aug)
train_predict = poly_model.predict(x_train)
test_predict = poly_model.predict(x_test)
train_mse = compute_mse(y_train, train_predict)
test_mse = compute_mse(y_test, test_predict)
train_loss.append(train_mse)
test_loss.append(test_mse)
plt.plot(degrees, train_loss, color='red', label='train_loss')
plt.plot(degrees, test_loss, color='green', label='test_loss')
plt.xlabel('degree')
plt.ylabel('mean square error')
plt.legend()
plt.savefig('loss_for_augmentation.png')
if __name__ == '__main__':
np.random.seed(1337)
x_train = [-3.0, -2.1, -0.9, 0.1, 1.2, 2.0, 3]
y_train = [2.5, 1.2, 1.1, -2.9, -0.7, -3.2, 1.3]
x_test = [-3.0, -2.7, -2.3, -2.0, -1.8, -1.6, -1.3, -1.0, -0.9, -0.6, -0.2,
0.1, 0.4, 0.7, 1.0, 1.2, 1.5, 1.8, 2.0, 2.3, 2.5, 2.7, 3.0]
y_test = [2.4, 2.1, 1.6, 1.1, 1.3, 1.0, 1.2, 1.0, 0.8, -0.2, -1.3, -2.3,
-2.7, -2.3, -1.5, -1.2, -1.5, -2.9, -2.5, -1.3, -1.1, -0.4, 1.1]
x_aug, y_aug = gauss_augmentation(x_train, y_train, 20, 0.4)
plot_original_dataset(x_train, y_train, x_test, y_test)
plot_augmented_dataset(x_train, y_train, x_test, y_test, x_aug, y_aug)
plot_no_augmentation_model(x_train, y_train, x_test, y_test)
plot_loss_for_overfitting(x_train, y_train, x_test, y_test)
plot_augmentation_model(x_train, y_train, x_aug, y_aug)
plot_loss_for_augmentation(x_train, y_train, x_test, y_test, x_aug, y_aug)
解释
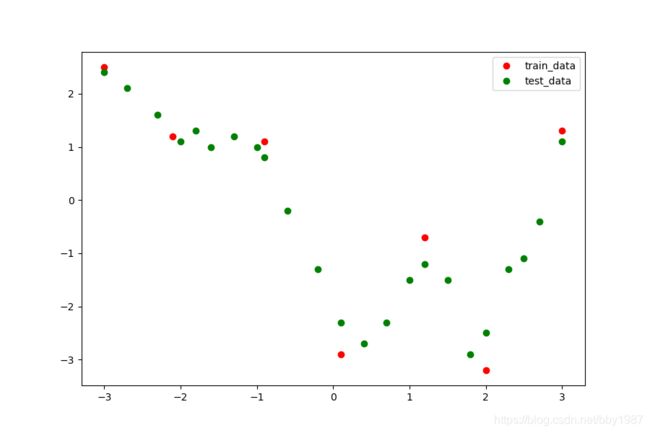
训练和测试数据
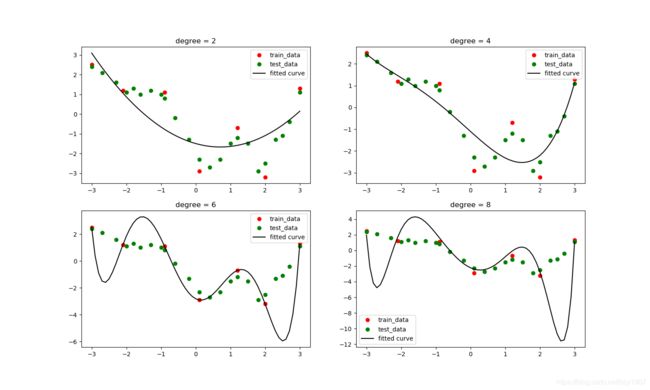
使用原始训练数据做曲线拟合
如图,随着多项式的次数(degree)从2变到6,拟合曲线对训练数据(红色点)的逼近程度越来越高,但是对测试数据的逼近程度却不是如此,特别是degree从4变到6以后,拟合曲线与测试数据的逼近程度反而增大,这就是过拟合现象。
当degree等于8时曲线反而不能完全穿过训练数据,关于此我们前面已有解释。
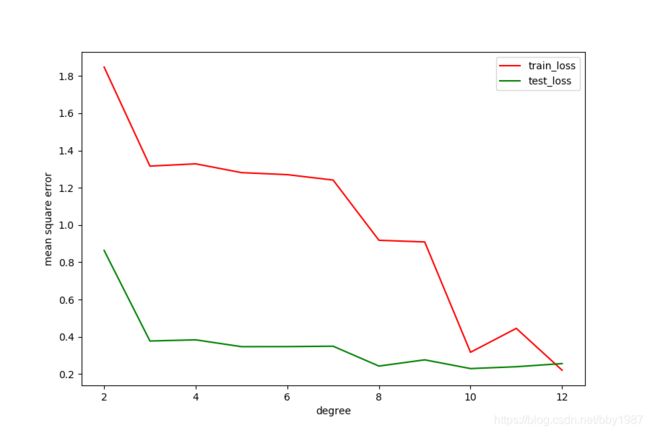
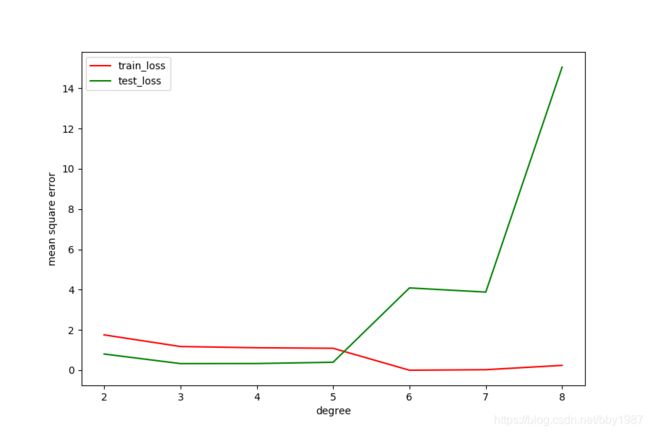
过拟合现象的loss表现
随着模型变大,测试集loss反而开始升高,这就是典型的过拟合现象在loss上的表现。
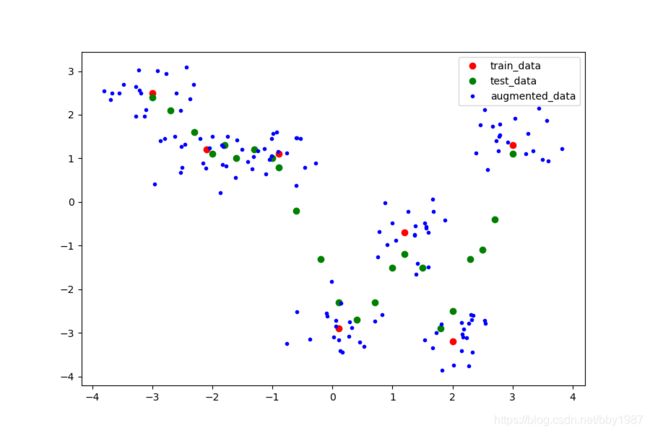
数据增强
数据增强方式是以训练集中的各个点为基准加上高斯分布的随机数,在其周围构造出一些随机点,这些随机点就是增强后的数据。此例中针对每个训练集中的点构造了20个增强的数据点。
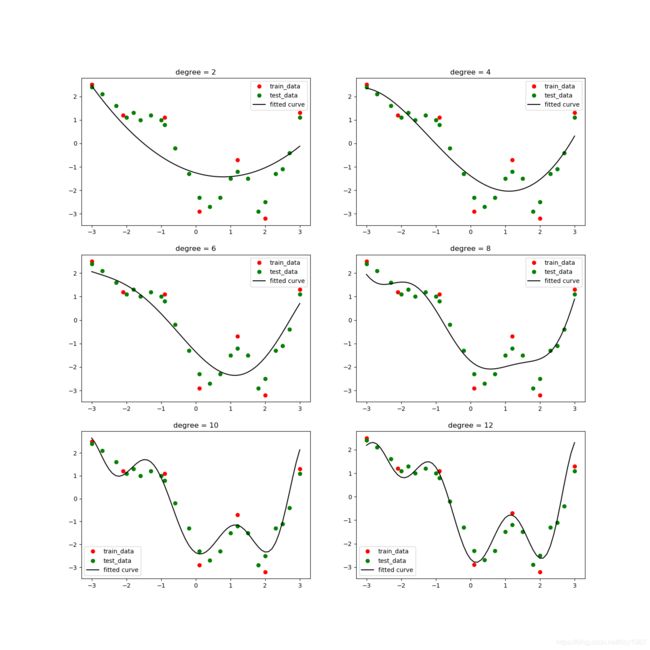
使用增强后的数据做曲线拟合
从图中可以看到,随着模型增大,拟合曲线不仅对训练集的逼近程度越来越高,对测试集的逼近程度也越来越高。这就是数据增强的威力:防止过拟合,提升在测试集上的效果;另外关键是,我们并没有额外地付出数据采集成本。