岭回归与Lasso回归
岭回归与Lasso回归
为什么引入岭回归
传统的多元线性回归可能存在多重共线性,岭回归可以看作是传统多元线性回归的升级版,可以打破多重共线性的限制。
和多元线性回归相似,岭回归的参数估计也是采用OLS(极大似然估计)原理
多元线性回归的参数估计:
β ^ = a r g min β ^ ∑ i = 1 n ( y i − x i ′ β ^ ) 2 \hat{\beta}=\mathrm{arg}\min_{\hat{\beta}}\sum_{i=1}^n(y_i-x_i^{\prime}\hat{\beta})^2 β^=argβ^mini=1∑n(yi−xi′β^)2
其中,
β ^ = ( β 1 ^ , β 2 ^ , ⋯ , β k ^ ) ′ \hat{\beta}=(\hat{\beta_1},\hat{\beta_2},\cdots,\hat{\beta_k})^{\prime} β^=(β1^,β2^,⋯,βk^)′
岭回归的参数估计:
β ^ = a r g min β ^ ∑ i = 1 n ( y i − x i ′ β ^ ) 2 + λ ∑ i = 1 n β i 2 ^ = a r g min β ^ ∑ i = 1 n ( Y − X ′ β ^ ) ′ ( Y − X ′ β ^ ) + λ ∑ i = 1 n β ′ ^ β ^ \hat{\beta}=\mathrm{arg}\min_{\hat{\beta}}\sum_{i=1}^n(y_i-x_i^{\prime}\hat{\beta})^2+\lambda\sum_{i=1}^n\hat{\beta_i^2}\\\qquad\qquad\qquad=\mathrm{arg}\min_{\hat{\beta}}\sum_{i=1}^n(Y-X^{\prime}\hat{\beta})^{\prime}(Y-X^{\prime}\hat{\beta})+\lambda\sum_{i=1}^n\hat{\beta^{\prime}}\hat{\beta} β^=argβ^mini=1∑n(yi−xi′β^)2+λi=1∑nβi2^=argβ^mini=1∑n(Y−X′β^)′(Y−X′β^)+λi=1∑nβ′^β^
可以得出, λ → 0 \lambda\to0 λ→0时,岭回归趋近于多元线性回归, λ → ∞ \lambda\to\infty λ→∞时, β ^ → 0 k × 1 \hat{\beta}\to0_{k\times 1} β^→0k×1
后面,有了理论推导,我们就知道,岭回归可以破除多重共线性的限制。
岭回归的理论推导
这里需要几个对向量求导的法则,这不需要大家掌握,只是为了方便推导
向量x的求导公式:
{ ∂ A X ∂ X = A T ∂ X T A X ∂ X = ( A + A T ) X \begin{cases}\frac{\partial AX}{\partial X}=A^T\\\frac{\partial X^TAX}{\partial X}=(A+A^T)X\end{cases} {∂X∂AX=AT∂X∂XTAX=(A+AT)X
令 L = a r g min β ^ ∑ i = 1 n ( Y − X ′ β ^ ) ′ ( Y − X ′ β ^ ) + λ ∑ i = 1 n β ′ ^ β ^ L=\mathrm{arg}\min_{\hat{\beta}}\sum_{i=1}^n(Y-X^{\prime}\hat{\beta})^{\prime}(Y-X^{\prime}\hat{\beta})+\lambda\sum_{i=1}^n\hat{\beta^{\prime}}\hat{\beta} L=argminβ^∑i=1n(Y−X′β^)′(Y−X′β^)+λ∑i=1nβ′^β^
则 ∂ L ∂ β ^ = − 2 X ′ Y + 2 X ′ X β ^ + 2 λ β ^ = 0 \frac{\partial L}{\partial \hat{\beta}}=-2X^{\prime}Y+2X^{\prime}X\hat{\beta}+2\lambda\hat{\beta}=0 ∂β^∂L=−2X′Y+2X′Xβ^+2λβ^=0得出 ( X ′ X + λ I ) β ^ = X ′ Y (X^{\prime}X+\lambda I)\hat{\beta}=X^{\prime}Y (X′X+λI)β^=X′Y
由于 X ′ X X^{\prime}X X′X半正定,则 X ′ X X^{\prime}X X′X的特征值均为非负数,加上 λ I \lambda I λI后, X ′ X + λ I X^{\prime}X+\lambda I X′X+λI的特征值均为正数,所以
β ^ = ( X ′ X + λ I ) − 1 X ′ Y ( λ > 0 ) \hat{\beta}=(X^{\prime}X+\lambda I)^{-1}X^{\prime}Y\quad(\lambda>0) β^=(X′X+λI)−1X′Y(λ>0)
我们可以通过下面几种方法选择 λ \lambda λ
岭迹分析
岭迹: λ \lambda λ从0到 + ∞ +\infty +∞变化,得到的 β ^ = ( β 1 ^ , β 2 ^ , ⋯ , β k ^ ) ′ \hat{\beta}=(\hat{\beta_1},\hat{\beta_2},\cdots,\hat{\beta_k})^{\prime} β^=(β1^,β2^,⋯,βk^)′中每个分量的变化曲线
这是我用Matlab跑出来的一个岭迹
岭迹法选择 λ \lambda λ的一般原则是:
(1)各回归系数的岭估计基本稳定
(2)用最小二乘估计时符号不合理的回归系数,其岭估计的符号变得合理
(3)回归系数没有不合乎经济意义的绝对值
(4)残差平方和增大不太多
可以选择 λ = 50 \lambda=50 λ=50
VIF法(方差膨胀因子)
VIF是方差膨胀因子,定义如下
假设现在有 k k k个自变量,那么第 m m m个自变量的 V I F m VIF_m VIFm定义为
V I F m = 1 1 − R 1 ∼ k \ m VIF_m=\frac{1}{1-R_{1\sim k\backslash m}} VIFm=1−R1∼k\m1
其中, R 1 s i m k \ m R_{1\\sim k\backslash m} R1simk\m是将第 m m m个自变量作为因变量,对剩下的 k − 1 k-1 k−1个自变量回归得到的拟合优度, V I F m VIF_m VIFm越大。说明第 m m m个变量和其他 k − 1 k-1 k−1个自变量相关性越强
回归模型的 V I F VIF VIF定义为
V I F = max { V I F 1 , V I F 2 , ⋯ , V I F k } VIF=\max \{VIF_1,VIF_2,\cdots,VIF_k\} VIF=max{VIF1,VIF2,⋯,VIFk}
如果 V I F > 10 VIF>10 VIF>10,可以认为存在多重共线性
可以不断增加 λ \lambda λ,直到所有的 β ^ < 0 \hat{\beta}<0 β^<0
可以使用stata计算VIF
例1:对下列数据进行多元回归,检验多重共线性
| 年份 | 单产 | 种子费 | 化肥费 | 农药费 | 机械费 | 灌溉费 |
|---|---|---|---|---|---|---|
| 1990 | 1017 | 106.05 | 495.15 | 305.1 | 45.9 | 56.1 |
| 1991 | 1036.5 | 113.55 | 561.45 | 343.8 | 68.55 | 93.3 |
| 1992 | 792 | 104.55 | 584.85 | 414 | 73.2 | 104.55 |
| 1993 | 861 | 132.75 | 658.35 | 453.75 | 82.95 | 107.55 |
| 1994 | 901.5 | 174.3 | 904.05 | 625.05 | 114 | 152.1 |
| 1995 | 922.5 | 230.4 | 1248.75 | 834.45 | 143.85 | 176.4 |
| 1996 | 916.5 | 238.2 | 1361.55 | 720.75 | 165.15 | 194.25 |
| 1997 | 976.5 | 260.1 | 1337.4 | 727.65 | 201.9 | 291.75 |
| 1998 | 1024.5 | 270.6 | 1195.8 | 775.5 | 220.5 | 271.35 |
| 1999 | 1003.5 | 286.2 | 1171.8 | 610.95 | 195 | 284.55 |
| 2000 | 1069.5 | 282.9 | 1151.55 | 599.85 | 190.65 | 277.35 |
| 2001 | 1168.5 | 317.85 | 1105.8 | 553.8 | 211.05 | 290.1 |
| 2002 | 1228.5 | 319.65 | 1213.05 | 513.75 | 231.6 | 324.15 |
| 2003 | 1023 | 368.4 | 1274.1 | 567.45 | 239.85 | 331.8 |
| 2004 | 1144.5 | 466.2 | 1527.9 | 487.35 | 408 | 336.15 |
| 2005 | 1122 | 449.85 | 1703.25 | 555.15 | 402.3 | 358.8 |
| 2006 | 1276.5 | 537 | 1888.5 | 637.2 | 480.75 | 428.4 |
| 2007 | 1233 | 565.5 | 2009.85 | 715.65 | 562.05 | 456.9 |
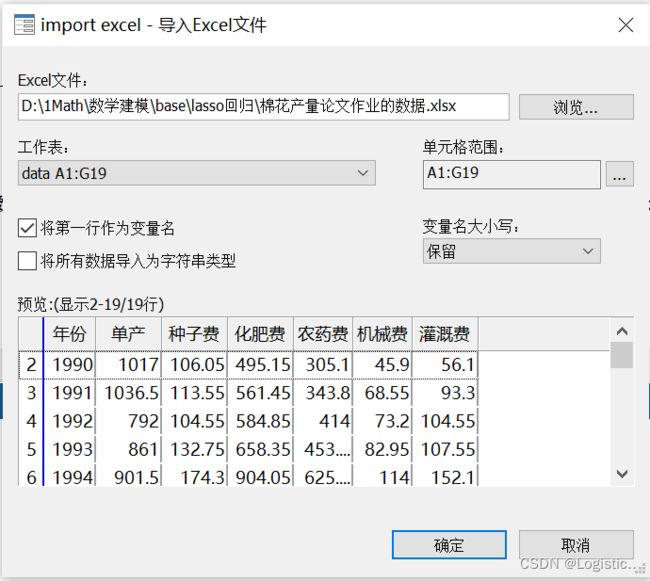
先导入数据
需要勾选“将第一行作为变量名”
进行多元线性回归可以输入语句
reg 单产 种子费 化肥费 农药费 机械费 灌溉费
在回归完成后输入下列语句
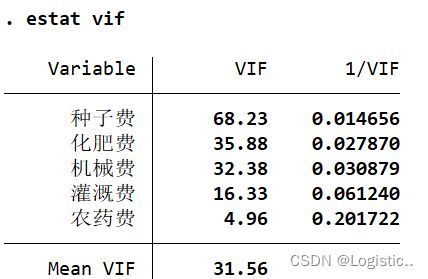
estat vif
VIF=68.23,说明多重共线性比较严重,需要剔除变量种子费,再继续回归。直到无多重共线性为止。
岭回归的Matlab实现
例2:对下列数据进行分析
| 序号 | 需求量 | 本品价格 | 竞品价格 | 平均收入水平 | 广告投入 |
|---|---|---|---|---|---|
| 1 | 12890 | 65 | 69.22 | 4343.17 | 1170 |
| 2 | 12850 | 65.9 | 70.67 | 4347.59 | 1162.26 |
| 3 | 13180 | 65.4 | 74.77 | 4356.44 | 1164.06 |
| 4 | 13785 | 65.34 | 75 | 4369.71 | 1193.13 |
| 5 | 13880 | 66 | 75 | 4387.4 | 1241.55 |
| 6 | 12680 | 69 | 77.29 | 4409.51 | 1254.15 |
| 7 | 13290 | 69 | 79.06 | 4436.05 | 1149.57 |
| 8 | 13498 | 69.25 | 81.37 | 4467.01 | 1200.06 |
| 9 | 11980 | 74.56 | 84 | 4502.4 | 1220.4 |
| 10 | 12085 | 78 | 91.61 | 4542.2 | 1082.7 |
data=[12890 65.00 69.22 4343.17 1170.00
12850 65.90 70.67 4347.59 1162.26
13180 65.40 74.77 4356.44 1164.06
13785 65.34 75.00 4369.71 1193.13
13880 66.00 75.00 4387.40 1241.55
12680 69.00 77.29 4409.51 1254.15
13290 69.00 79.06 4436.05 1149.57
13498 69.25 81.37 4467.01 1200.06
11980 74.56 84.00 4502.40 1220.40
12085 78.00 91.61 4542.20 1082.70];%数据矩阵
Y=data(:,1);%因变量组成的向量
[size_n,~]=size(data);%size_n表示样本容量
X=[ones(size_n,1),data(:,2:5)];%自变量矩阵左侧拼接全是1的向量
corr=corrcoef(data);%计算相关系数矩阵
Xtag={'需求量','本品价格','竞品价格','平均收入水平','广告投入'};
figure
heatmap(Xtag,Xtag,corr)%绘制相关系数热力图
beta=[];
[~,size_x]=size(X);
One_sq=linspace(0,100,1001);
for lambda=0:0.1:100
betanew=(X'*X+lambda*eye(size_x))^(-1)*X'*Y;
beta=[beta,betanew];%对每一个lambda,计算其回归系数
end
figure
for j=2:size_x
plot(One_sq,beta(j,:))%绘制岭迹图
hold on
end
legend(['\beta_' num2str(1)],['\beta_' num2str(2)],['\beta_' num2str(3)],['\beta_' num2str(4)])
title('岭迹分析')
xlabel('\lambda')
ylabel('\beta')
运行结果
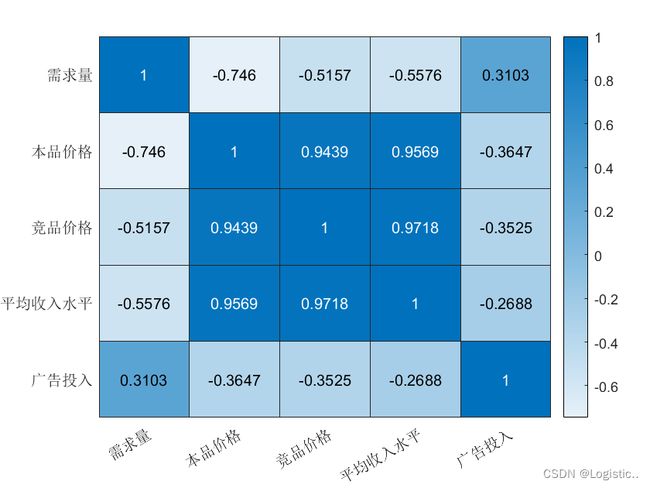
可以发现,竞品价格与本品价格之间相关性较强,竞品价格与平均收入水平之间相关性较强,平均收入水平与本品价格之间相关性较强。存在多重共线性,应该使用岭回归。
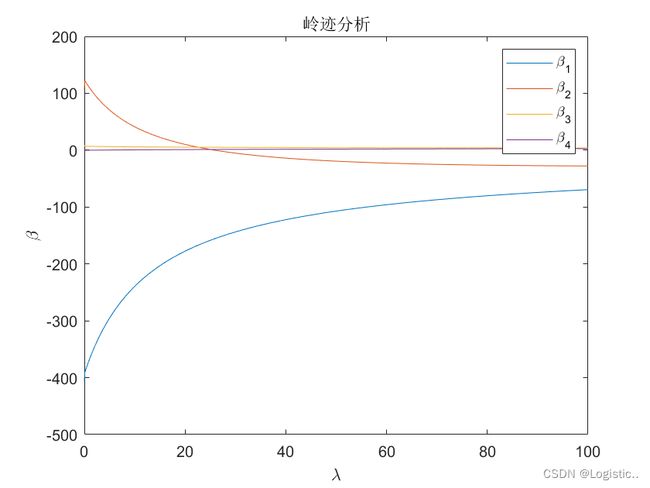
λ = 50 \lambda=50 λ=50时, y = 0.1992 − 107.1376 x 1 − 19.3472 x 2 + 4.4527 x 3 + 1.8729 x 4 y=0.1992-107.1376x_1-19.3472x_2+4.4527x_3+1.8729x_4 y=0.1992−107.1376x1−19.3472x2+4.4527x3+1.8729x4
逐步回归的进化——Lasso回归
Lasso回归的参数估计
β ^ = a r g min β ^ ∑ i = 1 n ( y i − x i ′ β ^ ) 2 + λ ∑ i = 1 n ∣ β i ∣ ^ \hat{\beta}=\mathrm{arg}\min_{\hat{\beta}}\sum_{i=1}^n(y_i-x_i^{\prime}\hat{\beta})^2+\lambda\sum_{i=1}^n\hat{|\beta_i|} β^=argβ^mini=1∑n(yi−xi′β^)2+λi=1∑n∣βi∣^
与岭回归相比,Lasso回归的出现也是为了克服多重共线性,最大的优点是可以把不重要的变量回归系数压缩到0,而岭回归的任何回归系数都不会压缩到0,这比较像升级版的逐步回归。
Lasso回归的stata实现
这里用的数据还是例1的数据
先在stata的命令行内输入命令
findit lassopack
点击click here to install
输入下列内容
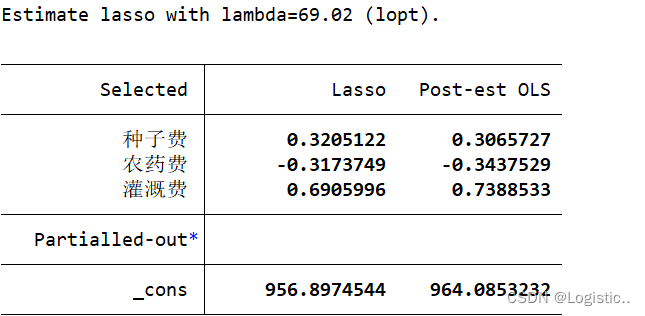
cvlasso 单产 种子费 化肥费 农药费 机械费 灌溉费,lopt seed(520)
tip:可以在变量窗口双击变量名,快速把变量输入到命令窗口
这说明,除了种子费,农药费,灌溉费,其他的变量均为引起多重共线性的变量,被剔除
我们的回归得出的模型如下:
y = 956.8974544 + 0.3205122 x 1 − 0.3173749 x 3 + 0.6905996 x 5 y=956.8974544+0.3205122x_1-0.3173749x_3+0.6905996x_5 y=956.8974544+0.3205122x1−0.3173749x3+0.6905996x5