K-hop消息传递图神经网络的表达能力有多强?
论文地址:How Powerful are K-hop Message Passing Graph Neural Networks
一.论文概述
近些年,从空域角度定义的图神经网络(Graph Neural Network, GNN)的工作较多。该类GNN大都遵从经典的消息传递范式,即节点聚合来自本身1-hop邻居的消息并结合自己的特征来生成自己新的节点特征,作者称之为1-hop消息传递。对GIN等工作有所了解的人都清楚,根据1-hop消息传递定义的GNN的表达能力上限为Weisfeiler-Lehman test(1-WL test)。为了获取更具表达能力的GNNs,有学者提出了 k k k-hop消息传递,该类GNN的表达能力显然超过1-hop消息传递,但缺乏理论分析。基于此现状,作者先从理论角度对 k k k-hop消息传递的表达能力进行了分析,并提出了 KP-GNN \text{KP-GNN} KP-GNN框架,该框架通过整合外围(peripheral)子图信息来进一步改进 k k k-hop消息传递。实验结果表明作者提出的 KP-GNN \text{KP-GNN} KP-GNN在众多benchmark数据集上都取得了有竞争力的结果。
二.K-hop消息传递
2.1 K-hop的定义
K K K-hop消息传递指的是图节点在更新自己的表示向量的时候,不是仅聚合来自邻居(1-hop)的消息,而是聚合来自 k k k-hop内所有邻居的消息。目前,有两种不同的 k k k-hop邻居定义:
- 基于图扩散(Graph Diffustion, GD) 的定义:图 G G G中节点 v v v的 k k k-hop邻居指经过 k k k步随机游走能达到 v v v的节点集,文中用 N v , G K , g d \mathcal{N}_{v, G}^{K, g d} Nv,GK,gd 表示。
- 基于最短路径距离(Shortest Path Distance, SPD) 的定义:图 G G G中节点 v v v的 k k k-hop邻居指**与其最短路径距离为 k k k**的节点集,文中用 N v , G K , s p d \mathcal{N}_{v, G}^{K, s p d} Nv,GK,spd表示。
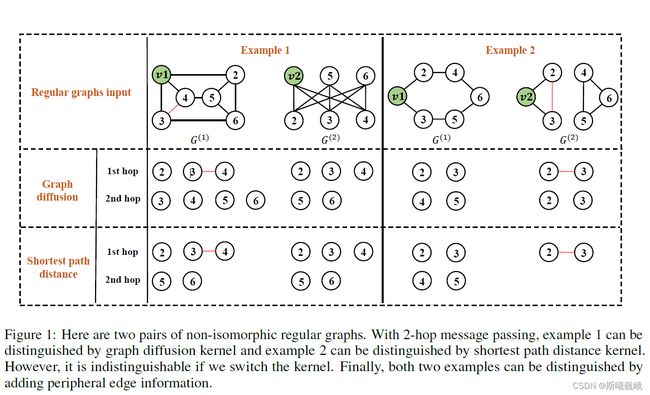
下图便包含了两种 k k k-hop邻居定义的示例:以Example1为例,对于 G ( 1 ) G^{(1)} G(1)中的节点 v 1 v1 v1,根据GD的定义其1-hop邻居包括 { 2 , 3 , 4 } \{2,3,4\} {2,3,4},2-hop邻居包括 { 2 , 3 , 4 , 5 } \{2,3,4,5\} {2,3,4,5},而根据 S P D SPD SPD的定义其1-hop邻居包括 { 2 , 3 , 4 } \{2,3,4\} {2,3,4},2-hop邻居包括 { 5 , 6 } \{5,6\} {5,6}。
2.2 K-hop消息传递框架
基于上述关于 k k k-hop邻居的定义,下面给出 k k k-hop消息传递框架的正式数学形式:
m v l , k = MES k l ( { { ( h u l − 1 , e u v ) ∣ u ∈ Q v , G k , t ) } ) , h v l , k = UPD k l ( m v l , k , h v l − 1 ) , h v l = COMBINE l ( { { h v l , k ∣ k = 1 , 2 , … , K } ) , . \begin{gathered} m_{v}^{l, k}=\operatorname{MES}_{k}^{l}(\{\{(h_{u}^{l-1}, e_{u v}) \mid u \in Q_{v, G}^{k, t})\}), \quad h_{v}^{l, k}=\operatorname{UPD}_{k}^{l}(m_{v}^{l, k}, h_{v}^{l-1}), \\ h_{v}^{l}=\operatorname{COMBINE}^{l}(\{\{h_{v}^{l, k} \mid k=1,2, \ldots, K\}),. \end{gathered} mvl,k=MESkl({{(hul−1,euv)∣u∈Qv,Gk,t)}),hvl,k=UPDkl(mvl,k,hvl−1),hvl=COMBINEl({{hvl,k∣k=1,2,…,K}),.
其中 t = { s p d , g d } t = \{spd, gd\} t={spd,gd},表示两种不同的 k k k-hop定义, m v l , k m_{v}^{l, k} mvl,k表示聚合来自 Q v , G k , t Q_{v, G}^{k, t} Qv,Gk,t的消息, h v l , k h_{v}^{l, k} hvl,k表示根据自己上一轮的特征和聚合来自 k k k-hop邻居的消息生成的节点 v v v的表示。从该公式可以看出,节点最终的表示 h v l h_{v}^{l} hvl是不同 k k k-hop的消息传递所得到的特征的组合。
2.3 K-hop消息传递框架的表达能力
结论:当 K > 1 K > 1 K>1时, K K K-hop消息传递严格比1-WL test表达能力更强大。
说明:对于 K K K-hop消息传递GNNs,只要两个节点在 K K K-hop内有区别, K K K-hop消息传递GNN就能区分。而这对于1-hop消息传递GNNs来说是确不一定,例如对于regular图,每个节点都具有相同的度,1-hop消息传递GNNs是区分不了的。以上图中的Example 2为例, G ( 1 ) G^{(1)} G(1)中的 v 1 v_1 v1和 G ( 2 ) G^{(2)} G(2)中的 v 2 v_2 v2的1-hop邻居是相同的,但是倘若使用 k k k-hop邻居,则通过2-hop邻居就可以将二者区分了。
2.4 K-hop消息传递框架的限制
作者指出现在提出的 k k k-hop消息传递框架存在一些缺陷。前面提到 K K K-hop的两种定义,作者指出不同定义的选择会影响 K K K-hop消息传递的表达能力。还是以上图以为,对于Example 1中的两个示例节点,若选用GD的定义,两个节点 v 1 v_1 v1和 v 2 v_2 v2的2-hop邻居是可以区分的,但若选择SPD,则这两个节点是没法去区分的,Example 2也类似。也就是说,没有哪种定义的2-hop消息传递可以同时区分两者。
三.KP-GNN框架详解
作者提出通过添加外围(peripheral)子图信息来提高 K K K-hop消息传递的表达能力。
3.1 外围边和外围子图
外围边指 Q v , G k , t Q_{v, G}^{k, t} Qv,Gk,t节点集中节点间的边,用符号来 E ( Q v , G k , t ) E(Q_{v, G}^{k, t}) E(Qv,Gk,t)表示。外围子图指由 Q v , G k , t Q_{v, G}^{k, t} Qv,Gk,t产生的诱导子图,用符号 G v , G k , t = ( Q v , G k , t , E ( Q v , G k , t ) ) G_{v, G}^{k, t}=(Q_{v, G}^{k, t}, E(Q_{v, G}^{k, t})) Gv,Gk,t=(Qv,Gk,t,E(Qv,Gk,t))来表示。
以Example 1为例,在1-hop中,左边的图中在节点3和节点4间存在一条边,即 E ( Q v 1 , G ( 1 ) 1 , t ) = { ( 3 , 4 ) } E(Q_{v_{1}, G^{(1)}}^{1, t})=\{(3,4)\} E(Qv1,G(1)1,t)={(3,4)},而对于右边的图 E ( Q v 2 , G ( 2 ) 1 , t ) = { } E(Q_{v_{2}, G^{(2)}}^{1, t})=\{\} E(Qv2,G(2)1,t)={} ,因此添加该信息可以成功的区分两个节点。
3.2 K-hop 外围子图增强图神经网络
KP-GNN \text{KP-GNN} KP-GNN与上述 K K K-hop消息传递的范式相差不大,区别在消息函数上:
h ^ v l , k = MES k l ( { { ( h u l − 1 , e u v ) ∣ u ∈ Q v , G k , t } , G v , G k , t ) \hat{h}_{v}^{l, k}=\operatorname{MES}_{k}^{l}(\{\{(h_{u}^{l-1}, e_{u v}) \mid u \in Q_{v, G}^{k, t}\}, G_{v, G}^{k, t}) h^vl,k=MESkl({{(hul−1,euv)∣u∈Qv,Gk,t},Gv,Gk,t)
从上述消息传递公式看出,在第 k k khop的消息步骤中,不仅聚合了邻居的信息,还聚合了第 k k k hop的外围子图。 KP-GNN \text{KP-GNN} KP-GNN的实现非常灵活,可以适用于任何图编码函数。为了在保持简单的同时最大化模型可以编码的信息,作者将消息函数实现为:
MES k l = MES k l , n o r m a l ( { ( h u l − 1 , e u v ) ∣ u ∈ Q v , G k , t } ) + ∑ c ∈ C 1 ∣ C ∣ ∑ ( i , j ) ∈ E ( Q v , G k , t ) c e i j , \operatorname{MES}_{k}^{l}=\operatorname{MES}_{k}^{l, normal}(\{(h_{u}^{l-1}, e_{u v}) \mid u \in Q_{v, G}^{k, t}\})+\sum_{c \in C} \frac{1}{|C|} \sum_{(i, j) \in E(Q_{v, G}^{k, t})_{c}} e_{i j}, MESkl=MESkl,normal({(hul−1,euv)∣u∈Qv,Gk,t})+c∈C∑∣C∣1(i,j)∈E(Qv,Gk,t)c∑eij,
其中 MES k l , normal \operatorname{MES}_{k}^{l, \text { normal }} MESkl, normal 表示原始GNN模型的消息函数, C C C是 G v , G k , t G_{v, G}^{k, t} Gv,Gk,t的连通分量集。 E ( Q v , G k , t ) c E(Q_{v, G}^{k, t})_{c} E(Qv,Gk,t)c是 G v , G k , t G_{v, G}^{k, t} Gv,Gk,t的第 c c c个连通分量对应的边集。这种实现帮助 KP-GNN \text{KP-GNN} KP-GNN不仅编码 E ( Q v , G k , t ) E(Q_{v, G}^{k, t}) E(Qv,Gk,t),而且能编码 G v , G k , t G_{v, G}^{k, t} Gv,Gk,t的部分信息(分量数)。
四.实验
作者以GIN作为baseline,并于其它表达能力更强的GNN(GIN-AK+,PNA,PPGN)进行了对比。对于作者的KP-GNN,作者实现了KP-GIN+,此外,作者还实现了KP-GIN的正常 K K K-hop版本(没有额外用外围子图增强)。
从实验结果可以看出,作者设计的模型 KP-GNN \text{KP-GNN} KP-GNN的框架能得到富有竞争力的结果。