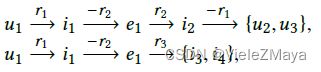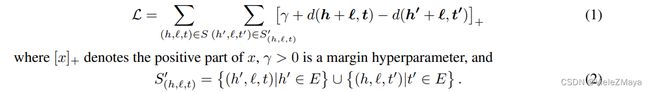推荐系统读书笔记（一）：KGAT
推荐系统读书笔记（一）：KGAT
原文：https://doi.org/10.1145/3292500.3330989
ABSTRACT
传统方法如因子分解机(FM)将user-item关系+侧信息建模其视为一个监督学习问题，由于忽略了实例或项目之间的关系，不足以从用户的集体行为中提取协作信号。
知识图谱通过高阶连通（用一个/多个链接属性连接两个item）能打破独立交互假设，利用节点（user、item、attribute均可）的邻居递归传播嵌入以细化本节点嵌入
注意力机制相比提取路径（耗费大量人工）、正则化隐式建模（无法捕获远程连接，无法解释高阶连通结果），在便捷性和显式融合高阶关系以优化推荐目标方面更优。
关键词
协同过滤，推荐，图神经网络，高阶连通性，嵌入传播，知识图
1 INTRODUCTION
1.1 CF和SL方法的局限性
CF方法无法对侧信息建模，无法应对矩阵稀疏的情况（解决：将侧信息建模为特征向量）
SL把每种关系单独建模，没有考虑协同信号（解决：知识图谱）
打个比方如下图，在用户u1和电影i1之间有一个交互，
CF方法：同样看过i1的相似用户：u4、u5
SL方法：属性也是为e1且关系也是r2的相似项：i2
很显然，SL方法没考虑到高阶连通性，即以下路径：
忽略了黄圈中的u2,u3看的i2都是e1导演的，灰圈中的i3,i4以r3和e1有联系
现在，我们希望：
综合两种方法，不仅可以对推荐进行互补，也使得user和item之间形成高阶关系
1.2 CKG引入及其问题解决
于是结合UI二部图和知识图谱，形成协同知识图谱（Collaborative Knowledge Graph ，CKG）
但新的问题又来咯：
- 节点会随着阶数增加而暴增，计算过载
- 高阶连通性会增加预测的不确定性，需要加权
以往方法：
1、基于路径：提取携带高阶信息的路径并将其输入预测模型
其中处理大量路径的方法：
（1）选择路径——没有对推荐目标的优化
（2）约束路径——需要领域知识且费人力，难搞
2、基于正则：设计额外损失隐式捕获KG结构，缺乏显式建模，既不能保证捕获远程连接，也不能解释高阶建模结果
于是，问题转化为：既要考虑高阶连通，又要考虑邻居加权——KGAT诞生
1.3 KGAT特点简述及工作提要
KGAT特点：
-
递归嵌入传播（Recursive embedding propagation）：根据节点近邻的嵌入更新节点的嵌入，并递归地进行嵌入传播以捕获线性时间复杂度的高阶连通性；
-
基于注意的聚集（Attention-based aggregation）：它利用神经注意机制来学习传播过程中每个邻居的权重，这样级联传播的注意权重可以揭示高阶连通性的重要性。
工作提要：
- 强调协同知识图谱中显式建模高阶关系，提供更好的item侧信息推荐
- 开发KGAT，在GCN下实现高阶关系显式建模
- 实验证明
2 TASK FORMULATION
UI二部图（User-Item Bipartite Graph）
用于描述user与item之间有无交互
G 1 = { ( u , y u i , i ) ∣ u ∈ U , i ∈ I ) } y u i = { 1 u 、 i 有 交 互 0 u 、 i 无 交 互 G_1 = \{(u,y_{ui}, i)|u ∈ U, i ∈ I)\}\\ y_{ui}=\left\{ \begin{array}{rcl} 1 & & {u、i有交互}\\ 0 & & {u、i无交互} \end{array} \right. G1={(u,yui,i)∣u∈U,i∈I)}yui={10u、i有交互u、i无交互
知识图谱（Knowledge Graph）
用于给item添加属性和外部知识，为有向图，
G 2 = { ( h , r , t ) ∣ h , t ∈ E , r ∈ R } G_2=\{(h, r, t)|h, t∈\Epsilon , r∈R\} G2={(h,r,t)∣h,t∈E,r∈R}
此外，还建立了一组UI对齐
A = { ( i , e ) ∣ i ∈ I , e ∈ E } A = \{(i, e)|i∈I, e∈E\} A={(i,e)∣i∈I,e∈E}
其中 ( i , e ) (i, e) (i,e)表示项目 i i i可以与KG中的实体 e e e对齐
协作知识图谱（CKG）
简而言之就是把UI二部图和知识图谱无缝衔接：
G 1 ′ = { ( u , I n t e r a c t , i ) ∣ I n t e r a c t ∈ y u i ∖ { 0 } } G 2 ′ = { ( h , r , t ) ∣ h , t ∈ E ′ , r ∈ R ′ } , E ′ = E ∪ U , R ′ = R ∪ { I n t e r a c t } G_1'=\{(u, Interact, i)|Interact∈{y_{ui}}\setminus\{0\}\}\\ G_2'=\{(h, r, t)|h, t ∈ E', r ∈R'\}, \\ E' = E ∪ U,\\ R'= R ∪ \{Interact\} G1′={(u,Interact,i)∣Interact∈yui∖{0}}G2′={(h,r,t)∣h,t∈E′,r∈R′},E′=E∪U,R′=R∪{Interact}
任务简述
输入：由G1和G2衔接得来的CKG
输出：一个预测UI之间交互概率的预测函数
高阶连通（High-Order Connectivity）
定义：将节点之间的l顺序连接定义为一个L跳关系路径
e 0 → r 1 e 1 → r 2 ⋅ ⋅ ⋅ → r L e L ( e l ∈ E ′ , r l ∈ R ′ ) e_0 \overset{r_1}{\rightarrow}e_1 \overset{r_2}{\rightarrow}···\overset{r_L}{\rightarrow}e_L\ \ \ (e_l ∈ E',r_l ∈ R') e0→r1e1→r2⋅⋅⋅→rLeL (el∈E′,rl∈R′)
CF侧重于描述与item有交互的用户之间的相似性
u 1 → r 1 i 1 → − r 1 u 2 → r 1 i 2 u_1 \overset{r_1}{\rightarrow}i_1\overset{-r_1}{\rightarrow}u_2\overset{r_1}{\rightarrow}i_2 u1→r1i1→−r1u2→r1i2
SL侧重于描述item的属性之间的相似性（因为是对每种关系单独建模，因此无法跨域）
u 1 → r 1 i 1 → r 2 e 1 → − r 2 i 2 u_1 \overset{r_1}{\rightarrow}i_1\overset{r_2}{\rightarrow}e_1\overset{-r_2}{\rightarrow}i_2 u1→r1i1→r2e1→−r2i2
仅靠上面其一都实现不了高阶连通
u 1 → r 1 i 1 → r 2 e 1 → − r 3 i 3 u_1 \overset{r_1}{\rightarrow}i_1\overset{r2}{\rightarrow}e_1\overset{-r_3}{\rightarrow}i_3 u1→r1i1→r2e1→−r3i3
3 METHODOLOGY
3.0 TransR回顾
TransE回顾：将关系视为低维向量空间中的头实体到尾实体的翻译操作，类似于拟合预测向量加法结果，即 h+r≈t。
要点：
-
entity需要在每次更新前进行归一化，这是通过人为增加embedding的norm来防止Loss在训练过程中极小化。
-
Loss函数(Hinge Loss Function) 为:
其中 [x]+ 表示x最小值为0, 即 [x]+=max(0,x) , S′ 表示负例的集合。
- 以norm = L2范数为例，求解正确三元组的h的相对于hinge loss function的梯度：
-
margin γ 的作用相当于是一个正确triple与错误triple之前的间隔修正，margin越大，则两个triple之前被修正的间隔就越大，则对于词向量的修正就越严格。
-
模型参数使用SGD优化
伪代码：
TransH（将关系投影到超平面上）方法解决 TransE 不能很好地处理 1-n、n-1 及 n-n 这样的复杂关系的问题，以及提出了 u n i f unif unif和 b e r n bern bern 的负采样方法（略）
TransR创新点是将 TransH 的投影到超平面更进一步——投影到空间
每个关系有自己一个独立的空间，如果要计算三元组 (h,r,t)的得分，要将 h 和 t投影到 r 所在的空间中来
3.1 嵌入层（针对CKG）
简要来说就是在CKG上用TransR模型（知识图谱嵌入方法）将实体和关系参数化为向量表示。
通过优化翻译，使得
e h r + e r ≈ e t r e h , e t ∈ R d e r ∈ R k 其 中 e h r , e t r 为 e h , e t 在 关 系 r 空 间 中 的 投 影 e^r_h + e_r ≈ e^r_t\\ e_h,e_t∈{\mathbb{R}}^d\\ e_r∈{\mathbb{R}}^k\\ 其中e^r_h,e^r_t 为 e_h,e_t 在关系r空间中的投影 ehr+er≈etreh,et∈Rder∈Rk其中ehr,etr为eh,et在关系r空间中的投影
可信度评分（分数越低，说明预测值与真实值越接近，三元组越可能为真）
g ( h , r , t ) = ∣ ∣ W r e h + e r − W r e t ∣ ∣ 2 2 g(h,r,t)=||W_re_h+e_r−W_re_t||^2_2 g(h,r,t)=∣∣Wreh+er−Wret∣∣22
其中 W r ∈ R k × d W_r∈\mathbb{R}^{k×d} Wr∈Rk×d是关系r的变换矩阵，它将实体从d维实体空间投影到k维关系空间
以如下损失函数 L K G L_{KG} LKG来区分有效、无效三元组的相对顺序
L K G = ∑ ( h , r , t , t ′ ) ∈ T − l n σ ( g ( h , r , t ′ ) − g ( h , r , t ) ) L_{KG} =\sum_{(h,r,t,t')∈\Tau}−lnσ(g(h,r,t')−g(h,r,t)) LKG=(h,r,t,t′)∈T∑−lnσ(g(h,r,t′)−g(h,r,t))
其中
T = { ( h , r , t , t ’ ) ∣ ( h , r , t ) ∈ G , ( h , r , t ′ ) ∉ G } T = \{(h, r, t, t ’)|(h, r, t) ∈ G, (h, r, t ')∉ G\} T={(h,r,t,t’)∣(h,r,t)∈G,(h,r,t′)∈/G}
( h , r , t ′ ) (h, r, t ') (h,r,t′)是通过随机替换有效三元组中的一个实体来形成的无效三元组
该层在三元组的粒度上对实体和关系进行建模，作为正则化器并将直接连接注入到嵌入表示中，从而提高了模型表示能力
3.2 注意力嵌入传播层（针对图卷积）
简要而言：高阶连通递归嵌入+加权
首先对于一个单层，它由三个部分组成：信息传播（information propagation）、知识意识注意（knowledge-aware attention）和信息聚合（information aggregation）
信息传播
一个实体可以出现在多个三元组里面，比如：
e 1 → r 2 i 2 → − r 1 u 2 e_1\overset{r_2}{\rightarrow}i_2\overset{-r_1}{\rightarrow}u_2 e1→r2i2→−r1u2
e 2 → r 3 i 2 → − r 1 u 2 e_2\overset{r_3}{\rightarrow}i_2\overset{-r_1}{\rightarrow}u_2 e2→r3i2→−r1u2
i 2 i_2 i2可以靠 e 1 、 e 2 e_1、e_2 e1、e2两个邻居的属性细化自身嵌入，从而递归地细化 u 2 u_2 u2的嵌入
为了模拟消息传播过程，现给定一个实体h， N h = { ( h , r , t ) ∣ ( h , r , t ) ∈ G } N_h = \{(h, r, t)|(h, r, t) ∈ G\} Nh={(h,r,t)∣(h,r,t)∈G}是其作为头实体的三元组（暂且称为ego-network），为了刻画h的一阶连通性结构，计算 N h N_h Nh的线性组合：
e N h = ∑ ( h , r , t ) ∈ N π ( h , r , t ) e t e_{N_h} =\sum_{(h,r,t)∈N}{π(h, r, t)e_t} eNh=(h,r,t)∈N∑π(h,r,t)et
其中 π ( h , r , t ) π(h, r, t) π(h,r,t)控制着边 ( h , r , t ) (h, r, t) (h,r,t)上每次传播的衰减因子，表示有多少信息从t传播到h
知识意识注意
π ( h , r , t ) = ( W r e t ) ⊤ t a n h ( ( W r e h + e r ) ) π(h, r, t) = (W_r e_t )^⊤tanh((W_r e_h + e_r )) π(h,r,t)=(Wret)⊤tanh((Wreh+er))
选取tanh作为非线性激活函数，使得注意力得分依赖于关系中 e h e_h eh和 e t e_t et之间的距离，换句话说就是二者离得越近，传的消息越多
然后通过 s o f t m a x softmax softmax函数将所有与h相连的三元组的系数归一化
π ( h , r , t ) = e x p ( π ( h , r , t ) ) ∑ ( h , r ′ , t ′ ) ∈ N h e x p ( π ( h , r ′ , t ′ ) ) π(h, r, t) = \frac{exp(π(h, r, t))}{\sum_{(h,r ',t ')∈N_h} {exp(π(h, r ', t '))}} π(h,r,t)=∑(h,r′,t′)∈Nhexp(π(h,r′,t′))exp(π(h,r,t))
与GCN、GraphSage将衰减因子定义为 1 ∣ N h ∣ ∣ N t ∣ \frac{1}{\sqrt{|N_h ||N_t |}} ∣Nh∣∣Nt∣1 或 1 ∣ N t ∣ \frac{1}{|N_t |} ∣Nt∣1的信息传播不同的是，此模型不仅利用了图的邻近性结构，而且给邻居进行加权以区分重要性
信息聚合
最后将原来的 e h e_h eh和传播得到的 e N h e_{N_h} eNh通过聚合函数 f ( ⋅ ) f(·) f(⋅)聚合成新的 e h e_h eh，即
e h ( 1 ) = f ( e h , e N h ) e^{(1)}_h =f (e_h, e_{N_h} ) eh(1)=f(eh,eNh)
其中，聚合函数有三种：
GCN Aggregator： e h e_h eh和 e N h e_{N_h} eNh直接相加，套一个d×d’（d’为变换大小）的可训练权重矩阵W，再套一个非线性激活函数
f G C N = L e a k y R e L U ( W ( e h + e N h ) ) f_{GCN} = LeakyReLU(W(e_h + e_{N_h} )) fGCN=LeakyReLU(W(eh+eNh))
GraphSage Aggregator：把上面的相加改为串联
f G r a p h S a g e = L e a k y R e L U ( W ( e h ∣ ∣ e N h ) ) f_{GraphSage} = LeakyReLU(W(e_h || e_{N_h} )) fGraphSage=LeakyReLU(W(eh∣∣eNh))
Bi-Interaction Aggregator：比上两个还多一个元素积 ⊙ \odot ⊙，使得被传播的信息对 e h e_h eh和 e N h e_{N_h} eNh之间的亲近性非常敏感，让相似的实体之间传递更多的消息
f B i − I n t e r a c t i o n = L e a k y R e L U ( W 1 ( e h + e N h ) ) + L e a k y R e L U ( W 2 ( e h ⊙ e N h ) ) f_{Bi-Interaction} = LeakyReLU(W_1(e_h + e_{N_h} )) + LeakyReLU(W_2(e_h \odot e_{N_h} )) fBi−Interaction=LeakyReLU(W1(eh+eNh))+LeakyReLU(W2(eh⊙eNh))
总而言之，嵌入传播层的优势在于显式地利用一阶连接信息来关联用户、项目和知识实体表示。
高阶传播
e h ( l ) = f ( e h ( l − 1 ) , e N h ( l − 1 ) ) e^{(l)}_ h = f (e^{(l−1)}_ h , e^{(l−1)}_ {N_h} ) eh(l)=f(eh(l−1),eNh(l−1))
e N h ( l − 1 ) = ∑ ( h , r , t ) ∈ N h π ( h , r , t ) e t ( l − 1 ) e^{(l−1)}_{N_h} = \sum_ {(h,r,t)∈{N_h}}{π(h, r, t)e^{(l−1)}_ t} eNh(l−1)=(h,r,t)∈Nh∑π(h,r,t)et(l−1)
其中 e t ( l − 1 ) e^{(l−1)}_ t et(l−1)为实体t在前面消息传播的过程中积累 ( l − 1 ) (l-1) (l−1)跳邻居的消息
e h ( 0 ) e^ {(0)} _h eh(0)作为 e h e_h eh在初始信息传播的集合，有助于在第 l l l层表示实体 h h h
因此对于如下高阶传播过程而言，在嵌入传播过程中可以将基于属性的协作信号无缝地注入到表示学习过程中：
u 2 → r 1 i 2 → − r 2 e 1 → r 2 i 1 → − r 1 u 1 u_2 \overset{r_1}{\rightarrow}i_2\overset{-r_2}{\rightarrow}e_1\overset{r_2}{\rightarrow}i_1\overset{-r_1}{\rightarrow}u_1 u2→r1i2→−r2e1→r2i1→−r1u1
其中来自 u 2 u_2 u2的高阶信息被显式的编码在 e u 1 ( 3 ) e_{u_1}^{(3)} eu1(3)中
3.3 模型预测
执行L层后，每个user u u u都对应多个表示 { e u ( 1 ) , . . . , e u ( L ) } \{e_u^{(1)},...,e_u^{(L)}\} {eu(1),...,eu(L)}，
每个item i i i也对应多个表示 { e i ( 1 ) , . . . , e i ( L ) } \{e_i^{(1)},...,e_i^{(L)}\} {ei(1),...,ei(L)}
不同层的输出强调了不同阶数的连通性信息。因此，采用层聚合机制，将每一步的表示连接成一个向量：
e u ∗ = e u ( 0 ) ∣ ∣ ⋅ ⋅ ⋅ ∣ ∣ e u ( L ) , e i ∗ = e i ( 0 ) ∣ ∣ ⋅ ⋅ ⋅ ∣ ∣ e i ( L ) e^∗_u = e^{(0)}_u ||···||e^{(L)}_u \ \ \ \ ,\ \ \ \ \ \ \ e^∗_i = e^{(0)}_ i ||· · · ||e^{(L)}_ i eu∗=eu(0)∣∣⋅⋅⋅∣∣eu(L) , ei∗=ei(0)∣∣⋅⋅⋅∣∣ei(L)
不仅可以通过执行嵌入传播操作来丰富初始嵌入，还可以通过调整L来控制传播强度。
最后对用户和物品表示进行内积，从而预测它们的匹配得分
y ^ ( u , i ) = ( e u ∗ ) ⊤ e i ∗ \hat{y}(u,i)=(e_u^∗)^⊤e_i^∗ y^(u,i)=(eu∗)⊤ei∗
3.4 损失函数与优化器
BPR损失：假设观察到的交互作用表明更多的用户偏好，应该比未观察到的交互作用赋予更高的预测值
L C F = ∑ ( u , i , j ) ∈ O − l n σ ( y ^ ( u , i ) − y ^ ( u , j ) ) L_{CF} = \sum_{(u,i, j)∈ O} − ln σ (\hat{y}(u, i) − \hat{y}(u, j)) LCF=(u,i,j)∈O∑−lnσ(y^(u,i)−y^(u,j))
其中 O = { ( u , i , j ) ∣ ( u , i ) ∈ R + , ( u , j ) ∈ R − } O = \{(u, i, j)|(u, i)∈R^+, (u, j)∈R^−\} O={(u,i,j)∣(u,i)∈R+,(u,j)∈R−}表示训练集， R + R^+ R+表示用户u与项目j之间的正交互集， R − R^− R−为采样的负交互集； σ ( ⋅ ) σ(·) σ(⋅)是sigmoid函数。
最后联合 L K G L_{KG} LKG和 L C F L_{CF} LCF，以及所有可训练的模型参数（嵌入、权重矩阵、层数等），再以λ进行 L 2 L_2 L2正则化防止过拟合后，得最终的损失函数：
L K G A T = L K G + L C F + λ ∣ ∣ Θ ∣ ∣ 2 2 L_{KGAT} = L_{KG} + L_{CF} + λ ||Θ||^2_2 LKGAT=LKG+LCF+λ∣∣Θ∣∣22
优化器：交替优化 L K G L_{KG} LKG和 L C F L_{C F} LCF，其中采用小批量Adam优化嵌入损耗和预测损耗。
4 EXPERIMENTS
4.0 Research Question
RQ1：性能比较——与最先进的知识感知推荐方法相比，KGAT的表现如何?
RQ2：消融研究——不同的组分(例如，知识图嵌入、注意机制和聚合器选择)如何影响KGAT的性能？
RQ3：实例验证——KGAT能否合理解释用户对物品的偏好？
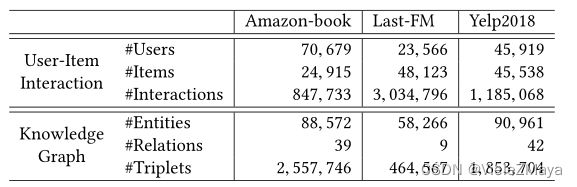
4.1 数据集
4.2 实验设置
4.2.1 评价指标
对于测试集中的每个用户，我们将用户未与之交互的所有项目视为负面项目。
然后除了训练集中的积极项目以外，每个方法输出用户对所有项目的偏好得分。
最后采用 r e c a l l @ K recall@K recall@K和 n d c g @ K ndcg@K ndcg@K两个指标来评估推荐结果。
4.2.2 Baselines
FM：基准分解模型，它考虑了输入之间的二阶特征交互。将用户的id、项目及其知识(即与之相连的实体)视为输入特征。
NFM：将FM丢到神经网络里面，还在输入特征上使用了一个隐藏层。
CKE：一种典型的基于正则化的方法，利用TransR派生的语义嵌入来增强矩阵分解
CFKG：在包含用户、项目、实体和关系的KG上应用TransE，将推荐任务转换为 ( u , i n t e r a c t , i ) (u, interact, i) (u,interact,i)三元组的预测
MCRec：基于路径的模型，提取合格的元路径作为用户和项之间的连接。
RippleNet：结合了基于正则化和基于路径的方法，通过在植根于每个用户的路径中添加项来丰富用户表示。
GC-MC：将GCN编码器用于UI二部图（本文作者把它应用于UI知识图谱），并使用了一个图卷积层，其中隐藏维数设置为嵌入大小。
4.2.3 参数设置
| 参数 | 值 |
|---|---|
| 嵌入大小 | 64（RippleNet 16） |
| Adam优化器批大小 | 1024 |
| 初始化器 | Xavier |
| 学习率 | {0.05,0.01,0.005,0.001} |
| L2 | {10−5,10−4，···，101,102} |
| Dropout | {0.0,0.1，··，0.8} |
| KGAT-层数L | 3 |
| KGAT-隐层大小 | {64,32,16} |
4.3 性能比较（RQ1）
KGAT在三个数据集上recall和ndcg都碾压所有Baseline
4.3.1 总体比较
① 碾压性优势：通过堆叠多个注意力嵌入传播层，KGAT能够显式地探索高阶连通性，从而有效地捕获协同信号
② 与固定权值的GC-MC相比，KGAT比它多了个注意力加权机制
③ SL方法（FM和NFM）大多数情况下比基于正则化的方法（CFKG和CKE）要强，因为：
-
SL利用的是与一个节点连接的所有邻居的嵌入（exploit the embeddings of its connected entities），而CFKG和CKE只是用其对齐实体的嵌入（only use that of its aligned entities）
-
FM和NFM中的交叉特性实际上是UI之间的二阶连接，而CFKG和CKE建模的是三元组粒度上的连接，没有涉及高阶连接。
④ 与FM相比，RippleNet验证了合并两跳邻居对细化user嵌入的重要性。因此指出了建模高阶连通性的积极作用。
⑤ 后面的就是baseline在不同数据集上的一些掰扯（略）
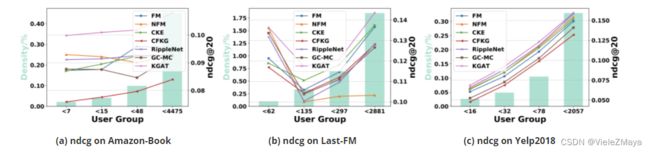
4.3.2 不同稀疏性比较
上图展示了KGAT及Baseline们在Amazon-book、Last-FM和Yelp2018中不同用户组（以Amazon-Book为例，用户数分别小于7、15、48和4475）上的ndcg@20走势对比，从中可知：
① KGAT在大多数情况下优于其他模型，特别是在Amazon-Book和Yelp2018这两个最稀疏的用户群上，再次验证了高阶连接建模的重要性：1)包含Baseline中使用的低阶连接，2)通过递归嵌入传播丰富了非活动用户的表示。
② KGAT在最密集的用户组(如Yelp2018的< 2057组)中相比其他Baseline的优势不是很明显，原因可能是有太多交互的用户的偏好太笼统，难以捕捉，同时高阶连通性会在用户首选项中引入更多的噪声，从而导致负面影响。
4.4 KGAT的研究（RQ2）
4.4.1 不同层数
- 证明了高阶传播的必要性
4.4.2 不同聚合函数
- 验证了双交互聚合器Bi-Interaction的有效性
4.4.3 不同KG嵌入与注意机制
消融研究：
- w/o KGE 禁用TransR（去除知识图谱嵌入）
- w/o Att 把 π ( h , r , t ) π(h, r, t) π(h,r,t)设为 1 / ∣ N h ∣ 1/|N_h | 1/∣Nh∣（去除注意力）
- w/o K&A综合前两种
① 去除知识图嵌入和注意力成分会降低模型的性能。
② 与去除注意力的方式相比，去除知识图谱嵌入的方式在大多数情况下性能更好。可能的原因：对所有邻居一视同仁，可能会引入噪声并误导嵌入传播过程。验证了图形注意力机制的必要性。
4.5 实例研究（RQ3）
KGAT捕捉了基于行为和基于属性的高阶连通性，这对推断用户偏好起着关键作用。
作者从Amazon-Book中随机选择了一个用户u208和一个相关项目i4293。图4显示了高阶连通性的可视化。
其中， u 208 → r 0 O l d M a n ’ s W a r → r 14 J o h n S c a l z i → − r 14 i 4293 u_{208} \overset{r_0}{\rightarrow}Old\ Man’s\ War\overset{r_{14}}{\rightarrow}John\ Scalzi\overset{-r_{14}}{\rightarrow}i_{4293} u208→r0Old Man’s War→r14John Scalzi→−r14i4293的注意力得分最高（左图实线）。
因此，推荐《The Last Colony》的原因是因为用户已经看过同一作者John Scalzi所写的《Old Man’s War》。
同样，项目知识的质量至关重要。可见，实体“English”与“Original Language”包含于一条路径中，过于笼统，无法提供高质量的解释。可以进行硬注意（hard attention），过滤掉信息量较小的实体。
5 CONCLUSION AND FUTURE WORK
结论：在这项工作中，作者探索CKG中具有语义关系的高阶连接，用于知识感知推荐（knowledge-aware recommendation）。
设计了一个新的框架KGAT，它以端到端方式显式地建模CKG中的高阶连接。它的核心是结合注意力机制的嵌入传播层，自适应地从节点的邻居传播嵌入以更新节点的表示。在三个真实数据集上的大量实验证明了KGAT的合理性和有效性。
这项工作探索了图神经网络在推荐中的潜力，是利用信息传播机制开发结构知识的初步尝试。
展望：除了知识图谱，在现实场景中也确实存在许多其他的结构信息，如社交网络和项目上下文。例如，把社交网络和CKG结合起来，可以研究社会是如何影响推荐的。另一个方向是进行可解释推荐研究，让信息传播与决策过程进行集成。
除论文本文及其Reference外，还参考网址：
https://blog.csdn.net/Caster_X/article/details/109448685
https://www.cnblogs.com/fengwenying/p/14561105.html
https://zhuanlan.zhihu.com/p/429988670
https://zhuanlan.zhihu.com/p/383217999