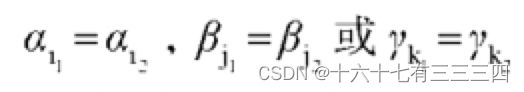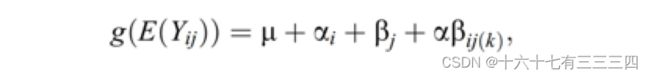什么是APC模型
一、APC模型的由来
在社会科学领域,社会科学家们总是很关心各种各样的社会变迁,例如在过去几十年间人们的健康程度(如某疾病的患病率)有着什么样的变化趋势,人们的社会态度(例如性别观念)又是怎么变化的……
这种变迁的时间效应又可以分解为三种不同类型的效应:
年龄效应:与年龄变化相关的、伴随生命历程以及因社会角色更替产生的变迁效应
例如:由于年龄增长,人的身体机能会逐渐衰弱,罹患各种疾病的风险会逐渐提高;年龄更大的人可能有更为保守的政治倾向态度(毕竟年轻人光脚不怕穿鞋的,老同志有房有车......)
时期效应:特定时期社会经济状况或发生的历史事件对所有年龄阶段的人口带来的影响
例如:某地突发的地震、海啸等自然灾害,对全部年龄人口死亡率的影响
队列效应:早年经历、社会因素或社会事件对某一特定出生队列带来的影响,是特定时期作用于特定年龄阶段人口的效应
例如:出生于战争时期的人之后在健康上表现更差;“wg”时期处于青年阶段的人在之后的职业轨迹上表现更劣
这三个效应里,最难理解的就是这个队列效应了。但是请注意,标粗的这一段话,特定时期作用于特定年龄阶段,也就是可以把队列效应理解为时期效应和年龄的效应的交互
研究社会变迁,就需要分离出其中的年龄效应、时期效应和队列效应
那么在量化研究中怎么分离不同效应,当然就是得用到回归了!
于是乎,就有了今天要讲的APC模型 A代表age 年龄 P代表period 时期 C代表cohort 队列
二、经典的APC模型
Mason(1973)最早讲了关于APC效应的方分析差模型,里面αi为第i个年龄组的年龄效应,πj为第j个时期的时期效应,γk 为第k个队列的队列效应
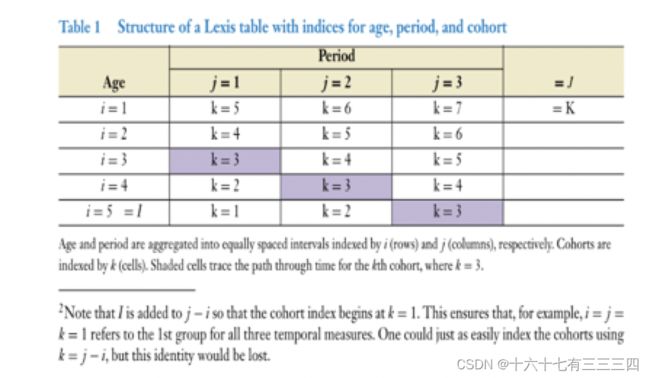
根据人口学知识,年龄、时期、队列这三者在数学上是完全共线的(如下图所示)
年龄=时期-队列
也就是说,我2001年生人(2001年出生队列),今年是2022年(时期),刚好21岁(年龄)……
21=2022-2001
这问题就来了,回归模型中的自变量是不能共线滴,这样的话模型就没办法估计出来了(简单理解一下,一个三元一次方程组(共三个方程),其中一个方程是X=Y+Z,方程组就没有唯一解了)
所以,这个经典的APC模型就有问题了。
三、APC模型的修正
模型有问题,搞学术总不能让方法不行憋死,正所谓有了问题就要解决问题!
于是社会学家、人口学家和统计学家们就开始脑筋想着怎么解决这个共线问题了
1、直接限定
解决的第一种就是直接限定的思路,既然模型估计不出来最优解是因为共线问题,那我把里面的参数限定一下不就行了?(就比如三元一次方程组只有两个方程,那我直接设定其中一个未知数等于某个常数,那不就能得到一组唯一解了)
于是乎有了两种方法
一种是两因素法,就是直接把年龄、时期、队列三个变量中的两个变量放进模型,那就不共线了(隐含的假设是其实是没给放进模型的那个变量效应为0)
另外一种是限定某两个待估计参数相等,这样也可以起到一样的效果
但新的问题来了,限定某个参数值往往需要强有力的理论依据,但这个强有力的理论往往是很难找的,那凭什么在这限定参数;并且,有研究也做过对比,发现如果用不同限定条件对结果的影响还挺大,也就是说模型稳健性结果其实是很差的………
2、IE估计量
既然直接限定法好像不太行得通,那就得找别的路子。既然是统计上的问题,那就从统计里找思路了。于是有学者就找到了一个叫做IE估计量的东西。
大致思路是,通过一系列的线性代数变换,把年龄时期队列这三个变量变成一个玩意,然后就能让这个模型估计出来了。(有点像主成分分析之类的统计技术,把好几个变量综合成一个变量)并且,最后发现这个估计量在统计上的性能还挺好,非常好地满足了可估计性、无偏性和有效性的估计量性质。
并且,IE估计量还能通过一系列的线性代数变换,又转换为年龄时期队列三个变量,这样就可以很好解释了。
但是这个问题也很大,虽然统计上性能不错,但是和社会事实就偏得有点远了……毕竟这个线性代数变换有点像黑箱,你怎么就能说通过这个变换变过去又变回来的那个系数是我们想要解释的那个系数呢?此外,也有研究发现这个估计量其实稳健性挺差,模型稍微有点变动结果也跟着变着很大……所以,这个方法好像也不太行
3、分层随机交叉效应模型
接下来这种方法就是分层模型了,这种方法借用混合/分层模型中的思想,假设年龄是属于个体层次的变量,同一个时期或队列的人群经历的社会事件和人生经历是相似的,在群体层面上会有相似的影响,时期和队列都可以视为群体层次的变量。年龄、时期、队列不再是同一个层面的变量,而是产生了嵌套关系。
这种方法一方面其实在数学上很好解决了共线性中的问题,另一方面也很符合理论。毕竟年龄效应确实是每个人自身的特质,而时期和队列讲的东西确实更反映的是群体层面上的效应。
并且,近些年来,这个方法在实证层面的研究确实开展得如火如荼。
但是……就像前面方法所说的但是,这个方法也是有问题的。有学者就根据一系列的数学证明,发现分层APC模型可能具有更大的秩亏(有更多限定),对时期或队列的随机效应设定本质上将该效应的线性效应以及随机截距的估计约束为零(如果用这个模型去画时期或队列的边际效应图,会发现它不会有一个恒定的趋势,而是一会上升,一会下降……)
4、虚拟变量分组法——间接限定
虚拟变量分组法,顾名思义,既然线性估计不出来,那我就用些tricky的方法,不把连续变量放进去了。例如,把时期和年龄操作成五年一组或者五岁一组的,这样放进去也不共线了。
当然,这种方法背后其实也是参数限定的一种表现。因为放到一组的那些年龄或者时期效应就共享一个系数了,也即默认它们的系数相等
5、代理变量法
代理变量法的思路就很类似于工具变量,核心思想是,寻找一个非时间变量来替代时间变量A/P/C,解决模型的不可识别问题。
这一方面用在APC模型里其实是很恰当的,因为虽然我们讲年龄时期队列效应,但事实上,例如我们讲时期效应并不是时期本身在起作用,而是在这个时期发生了某件历史事件产生的作用。所以,如果能直接找到那个机制变量,结果当然是更好的。
但问题是,就像工具变量一样,这个变量也是很难找的
例如,如果我们寻找一个非时间变量M来代替时间变量P
对应的假设是:变量M与其他两个时间变量A和C无关;M是连接P和因变量Y的唯一机制
不过有学者也认为这两个假设其实是可以放宽的
6、边界的部分识别法
这个方法的意思是,虽然我没有办法得到一组关于A、P、C的唯一解,但其实我可以得到一个关于它们系数的解线(对应到三维平面中的解空间)。
也就是说,我得不到点估计,那我就退而求其次,我只想要一个区间估计。
这样的话,我可以根据估计出来的解线,再结合我可以从理论以及模型中得到的限定条件,进一步缩小解线的范围。
例如,某个慢性疾病的患病率会随着年龄的上升而上升,那我们就能知道年龄的系数是正的,那我们就能缩小解线的部分范围。
缩小后的解线范围对于我们理解社会事实也是有帮助的。
7、APC-I模型
最后一个就是APC的交互效应模型,这个模型的开发者就直接否定了经典的APC模型,认为原来的方差分析模型是错的。因为她认为从理论上来讲,队列效应本身就不和年龄效应以及时期效应独立,它就是特定时期作用于特定年龄的一个结果(回到最开始讲什么是队列效应)
所以在统计上,我们把队列效应理解为年龄和时期效应的交互项就好了
这张图即为APC-I的一个模型设定形式
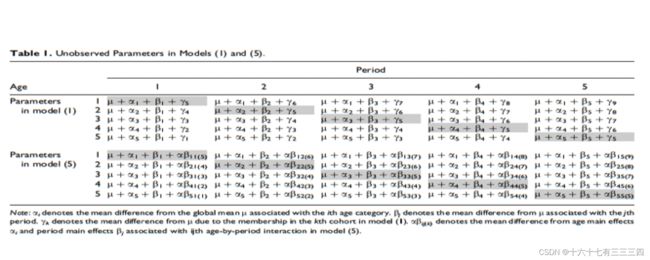
这张图为经典的APC模型(APC-C)和APC交互模型(APC-I)对不同效应的理解差异,上面是APC-C,下面是APC-I
附:不同模型在stata中的操作方式
IE估计量就用apc_ie这个命令
分层交叉随机效应模型用和分层模型一样的命令就好了:mixed
APC-I模型就把队列处理成年龄和时期的交互项进行估计
虚拟分组法对变量进行不同的操作化
一些参考文献:
Ryder, N. B. (1985). The cohort as a concept in the study of social change. In Cohort analysis in social research (pp. 9-44). Springer, New York, NY.
Mason, K. O., Mason, W. M., Winsborough, H. H., & Poole, W. K. (1973). Some methodological issues in cohort analysis of archival data. American sociological review, 242-258.
Fosse, E., & Winship, C. (2019). Analyzing age-period-cohort data: A review and critique. Annual Review of Sociology, 45(1), 467-492.
Luo, L., & Hodges, J. S. (2022). The age-period-cohort-interaction model for describing and investigating inter-cohort deviations and intra-cohort life-course dynamics. Sociological Methods & Research, 51(3), 1164-1210.
吴晓刚 & 李晓光.(2021).中国城市劳动力市场中教育匹配的变迁趋势——基于年龄、时期和世代效应的动态分析. 中国社会科学(02),102-122+206-207.
Luo, L., & Hodges, J. S. (2016). Block constraints in age–period–cohort models with unequal-width intervals. Sociological Methods & Research, 45(4), 700-726.
Holford, T. R. (2014). Age–period–cohort analysis. Wiley StatsRef: Statistics Reference Online, 1-25.
Li, T., & Xie, Y. (2022). The evolution of demographic methods. Social Science Research, 107, 102768.
Winship, C., & Harding, D. J. (2008). A mechanism-based approach to the identification of age–period–cohort models. Sociological methods & research, 36(3), 362-401.
Mason, W. M., & Smith, H. L. (1985). Age-period-cohort analysis and the study of deaths from pulmonary tuberculosis. In Cohort analysis in social research (pp. 151-227). Springer, New York, NY.
Fu, W. J. (2000). Ridge estimator in singulah oesiun with application to age-period-cohort analysis of disease rates. Communications in statistics-Theory and Methods, 29(2), 263-278.
Yang, Y., Schulhofer-Wohl, S., Fu, W. J., & Land, K. C. (2008). The intrinsic estimator for age-period-cohort analysis: what it is and how to use it. American Journal of Sociology, 113(6), 1697-1736.