《机器学习》学习笔记3:逻辑回归与正则化
Week3 逻辑回归与正则化
基于吴恩达《机器学习》课程
参考黄海广的笔记
本篇博客为第三周的内容。
W3 逻辑回归与正则化
6 逻辑回归(Logistic Regression)
6.1 分类问题的假设函数
逻辑回归算法实际上是一种分类算法,它适用于标签 y y y 取值离散的情况,例如0 表示负向类,1 表示正向类。逻辑回归算法要使输出值永远在0到 1 之间,所以假设函数模型为:
h θ ( x ) = g ( θ T X ) h_\theta \left( x \right)=g\left(\theta^{T}X \right) hθ(x)=g(θTX)
其中: X X X 代表特征向量, g g g 代表逻辑函数(logistic function) ,公式为: g ( z ) = 1 1 + e − z g\left( z \right)=\frac{1}{1+{{e}^{-z}}} g(z)=1+e−z1,作用是将一个实数映射到0~1之间。代入后可得:
h θ ( x ) = 1 1 + e − θ T X h_\theta \left( x \right)=\frac{1}{1+{{e}^{-\theta^{T}X}}} hθ(x)=1+e−θTX1
h θ ( x ) h_\theta \left( x \right) hθ(x)的作用是,对于给定的输入变量 x x x,根据选择的参数 θ \theta θ计算输出变量 y = 1 y=1 y=1的可能性即 h θ ( x ) = P ( y = 1 ∣ x ; θ ) = 1 − P ( y = 0 ∣ x ; θ ) h_\theta \left( x \right)=P\left( y=1|x;\theta \right)=1-P\left(y=0|x;\theta \right) hθ(x)=P(y=1∣x;θ)=1−P(y=0∣x;θ)
对于逻辑函数 g ( z ) g(z) g(z):$z≥0 $时 g ( z ) ≥ 0.5 g(z)≥0.5 g(z)≥0.5, z < 0 z<0 z<0 时 g ( z ) < 0.5 g(z)<0.5 g(z)<0.5,又 z = θ T x z={\theta^{T}}x z=θTx,即:
θ T x ≥ 0 {\theta^{T}}x≥0 θTx≥0 时,预测 y = 1 y=1 y=1 , θ T x < 0 {\theta^{T}}x<0 θTx<0 时,预测 y = 0 y=0 y=0。
所以 θ T x = 0 {\theta^{T}}x=0 θTx=0 这条线便是我们模型的分界线,将预测为1的区域和预测为 0的区域分隔开,即为判定边界(decision boundary) 。根据需要可以用非常复杂的模型来适应非常复杂形状的判定边界。
6.2 逻辑回归代价函数和梯度下降
线性回归的代价函数为: J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{1}{2}{{\left( {h_\theta}\left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}} J(θ)=m1i=1∑m21(hθ(x(i))−y(i))2 。但是当我们将 h θ ( x ) = 1 1 + e − θ T x {h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}} hθ(x)=1+e−θTx1这种非线性函数代入到这个代价函数中时,我们得到的是一个非凸函数(non-convexfunction) ,有许多局部最小值,这将影响梯度下降算法寻找全局最小值(凸性分析)。
我们重新定义逻辑回归的代价函数为: J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{{Cost}\left( {h_\theta}\left( {x}^{\left( i \right)} \right),{y}^{\left( i \right)} \right)} J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))
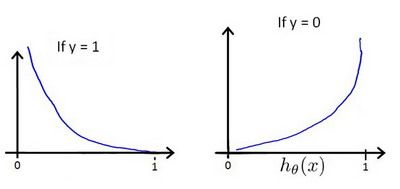
其中: C o s t ( h θ ( x ) , y ) = { − l n ( h θ ( x ) ) ( y = 1 ) − l n ( 1 − h θ ( x ) ) ( y = 0 ) Cost\left( {h_\theta}\left( x \right),y \right)=\begin{cases} -ln\left({h_\theta}\left( x \right) \right)\qquad (y=1) \\ -ln\left( 1-{h_\theta}\left( x \right) \right)\qquad (y=0) \end{cases} Cost(hθ(x),y)={−ln(hθ(x))(y=1)−ln(1−hθ(x))(y=0),表示实际标签是y时,输出预测值 h θ ( x ) {h_\theta}\left( x \right) hθ(x)所付出的代价。 h θ ( x ) − C o s t ( h θ ( x ) , y ) {h_\theta}\left( x \right)- Cost\left( {h_\theta}\left( x \right),y \right) hθ(x)−Cost(hθ(x),y)图像如下所示,即输出值越不符合标签y付出代价越大。
合并式子得到: C o s t ( h θ ( x ) , y ) = − y × l n ( h θ ( x ) ) − ( 1 − y ) × l n ( 1 − h θ ( x ) ) Cost\left( {h_\theta}\left( x \right),y \right)=-y\times ln\left( {h_\theta}\left( x \right) \right)-(1-y)\times ln\left( 1-{h_\theta}\left( x \right) \right) Cost(hθ(x),y)=−y×ln(hθ(x))−(1−y)×ln(1−hθ(x))
实际上这个式子由极大似然估计法 得到,这是一种为不同已经确定的模型快速寻找参数的方法。
故逻辑回归的代价函数为:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
接下来要找尽量让 J ( θ ) J\left( \theta \right) J(θ) 取得最小值的参数 θ \theta θ,使用梯度下降法 。
θ j : = θ j − α ∂ ∂ θ j J ( θ ) {\theta_{j}}:={\theta_{j}}-\alpha \frac{\partial }{\partial {\theta_{j}}}J ( \theta) θj:=θj−α∂θj∂J(θ)
代入 J ( θ ) J\left( \theta \right) J(θ)求偏导得:
** Repeat ** until convergence {
θ j : = θ j − α 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) ) {\theta_{j}}:={\theta_{j}}-\alpha\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}_j^{(i)}} \right)} θj:=θj−αm1i=1∑m((hθ(x(i))−y(i))⋅xj(i))
} 每次要同时更新 θ 0 {\theta_{0}} θ0… θ n {\theta_{n}} θn。
虽然更新参数的形式看起来基本相同,但由于假设 h θ ( x ) {h_\theta}\left( x \right) hθ(x)的定义完全不同,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
如果你的特征范围差距很大,那么用特征缩放 的方法,能梯度下降收敛更快。
6.3 高级优化方法
梯度下降并不是我们可以使用的唯一最小化代价函数的算法。例如共轭梯度法、BFGS (变尺度法 ) 和L-BFGS (限制变尺度法 ) ,它们比梯度下降法复杂很多,通常不需要手动选择学习率 α \alpha α(内部有线性搜索 (line search )算法,自动尝试并选择一个好的学习速率 a a a,甚至可以每次迭代选择不同的学习速率),往往最终比梯度下降收敛得快多了。
这些算法过于复杂,不用自己实现。首先写一个函数计算和返回代价函数 J ( θ ) J(\theta) J(θ)和所有偏导数项 ∂ ∂ θ j J ( θ ) \frac{\partial }{\partial {\theta_j}}J\left( \theta \right) ∂θj∂J(θ),然后调用算法库即可。
6.4 多类别分类:一对多
标签 y y y取值多于2个时,就成为了多分类问题,此时采用“一对多”方法。
有 1 ~ n 1~n 1~n个类时,将其中一个作为正类,其他所有作为负类,按逻辑回归方法得到模型 h θ ( 1 ) ( x ) h_\theta^{\left( 1 \right)}\left( x \right) hθ(1)(x),然后将第二个作为正类,其他作为负类得到 h θ ( 2 ) ( x ) h_\theta^{\left( 2 \right)}\left( x \right) hθ(2)(x),直到所有的类别都这分过类。
我们可以得到一系列的模型: h θ ( i ) ( x ) = p ( y = i ∣ x ; θ ) h_\theta^{\left( i \right)}\left( x \right)=p\left( y=i|x;\theta \right) hθ(i)(x)=p(y=i∣x;θ)其中: i = ( 1 , 2 , 3.... n ) i=\left( 1,2,3....n \right) i=(1,2,3....n)
在我们需要做预测时,输入一个新的 x x x值,我们将所有的分类机都运行一遍,然后选择 h θ ( i ) ( x ) h_\theta^{\left( i \right)}\left( x \right) hθ(i)(x) 最大的作为输出,即选择可能性最高的输出。
7 正则化
7.1 过拟合问题
特征过多或者选择的多项式次数越高,对于已有训练集的拟合度越好,但是泛化能力变差,推广预测新数据的能力变差,这就是过拟合(over-fitting) 的问题。相反即为欠拟合。
一般对于过拟合问题的处理办法有:
-
丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙,例如 Principal Component Analysis (PCA 主成分分析)。
-
正则化 。 保留所有的特征,但是减少参数的大小或量级(magnitude )。
7.2 正则化的代价函数
回归问题中如果我们的模型是: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 + θ 4 x 4 4 {h_\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3}+{\theta_{4}}{x_{4}^4} hθ(x)=θ0+θ1x1+θ2x22+θ3x33+θ4x44,高次项导致了过拟合的产生,所以我们要做的就是在一定程度上减小这些参数 θ \theta θ的值,这就是正则化基本方法。
若要减少 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4的大小,我们要做的便是修改代价函数,对 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4设置一点惩罚:
min θ 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 θ 3 2 + 10000 θ 4 2 ] \underset{\theta }{\mathop{\min }}\,\frac{1}{2m}[\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}+1000\theta _{3}^{2}+10000\theta _{4}^{2}]} θmin2m1[i=1∑m(hθ(x(i))−y(i))2+1000θ32+10000θ42]
假设函数的参数值 θ \theta θ越小,得到的函数图像越光滑简单,越不容易出现过拟合。
如果我们并不知道其中哪些特征要惩罚,我们就对所有的特征进行惩罚,即在代价函数后面添加一项,用于收缩每个参数:
J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J\left( \theta \right)=\frac{1}{2m}[\sum\limits_{i=1}^{m}{{{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}+\lambda \sum\limits_{j=1}^{n}{\theta_{j}^{2}}]} J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
其中 λ \lambda λ称为正则化参数 (Regularization Parameter )。 根据惯例,我们不对 θ 0 \theta_{0} θ0进行惩罚,所以求和从1开始。但实际上惩罚也没什么影响。
λ λ λ要做的就是控制在两个不同的目标中的平衡关系。第一个目标就是我们想要更好地拟合训练数据。第二个目标是我们想要保持参数值较小。
如果选择的正则化参数 λ \lambda λ 过大,则会把所有的参数都最小化了,导致模型变成 h θ ( x ) = θ 0 {h_\theta}\left( x \right)={\theta_{0}} hθ(x)=θ0,造成欠拟合。所以我们要取一个合理的 λ \lambda λ 的值。
7.3 正则化的线性回归
正则化线性回归的代价函数为:
J ( θ ) = 1 2 m ∑ i = 1 m [ ( ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ) ] J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{[({{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}+\lambda \sum\limits_{j=1}^{n}{\theta _{j}^{2}})]} J(θ)=2m1i=1∑m[((hθ(x(i))−y(i))2+λj=1∑nθj2)]
我们未对 θ 0 \theta_0 θ0进行正则化,所以梯度下降算法应分两种情形:
R e p e a t Repeat Repeat u n t i l until until c o n v e r g e n c e convergence convergence{
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ) {\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{0}^{(i)}}) θ0:=θ0−am1i=1∑m((hθ(x(i))−y(i))x0(i))
θ j : = θ j − a [ 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}] θj:=θj−a[m1i=1∑m((hθ(x(i))−y(i))xj(i)+mλθj] ( f o r for for j = 1 , 2 , . . . n j=1,2,...n j=1,2,...n)
}
对上面的算法中 j = 1 , 2 , . . . , n j=1,2,...,n j=1,2,...,n时的更新式子进行调整可得:
θ j : = θ j ( 1 − a λ m ) − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta_j}:={\theta_j}(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}} θj:=θj(1−amλ)−am1i=1∑m(hθ(x(i))−y(i))xj(i)
由于 ( 1 − a λ m ) < 1 (1-a\frac{\lambda }{m})<1 (1−amλ)<1,可看出正则化线性回归的梯度下降算法每次都在原有算法更新规则的基础上令 θ \theta θ值减少了一个额外的值。
同样也可以利用正规方程来求解正则化线性回归模型:
θ = ( X T X + λ [ 0 1 . . . 1 ] ) − 1 X T y \theta ={{\left({X^T}X+\lambda \begin{bmatrix} {0} & & & \\ & 1 & & \\ & & ...& \\ & & & 1\\ \end{bmatrix} \right)}^{-1}}{X^{T}}y θ=⎝⎜⎜⎛XTX+λ⎣⎢⎢⎡01...1⎦⎥⎥⎤⎠⎟⎟⎞−1XTy 。
图中的矩阵尺寸为 ( n + 1 ) ∗ ( n + 1 ) (n+1)*(n+1) (n+1)∗(n+1)。
只要 λ > 0 \lambda >0 λ>0,就可以保证 X T X + λ [ 0 1 . . . 1 ] {X^T}X+\lambda\begin{bmatrix}{0} & & & \\& 1 & & \\& & ...& \\& & & 1\\\end{bmatrix} XTX+λ⎣⎢⎢⎡01...1⎦⎥⎥⎤一定是可逆的,这就是正则化解决矩阵不可逆的方法。
7.4 正则化的逻辑回归
给逻辑回归的代价函数增加一个正则化的表达式,得到:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
要最小化该代价函数,通过求导,得出梯度下降算法为:
R e p e a t Repeat Repeat u n t i l until until c o n v e r g e n c e convergence convergence{
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ) {\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{0}^{(i)}}) θ0:=θ0−am1i=1∑m((hθ(x(i))−y(i))x0(i))
θ j : = θ j − a [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}] θj:=θj−a[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj] ( f o r for for j = 1 , 2 , . . . n j=1,2,...n j=1,2,...n)
}
看上去同线性回归一样,但是 h θ ( x ) = g ( θ T X ) {h_\theta}\left( x \right)=g\left( {\theta^T}X \right) hθ(x)=g(θTX),所以与线性回归不同。
使用高级优化方法时, J ( θ ) J\left( \theta \right) J(θ)和 ∂ ∂ θ j J ( θ ) \frac{\partial }{\partial {\theta_j}}J\left( \theta \right) ∂θj∂J(θ)都用正则化的式子,注意 θ 0 \theta_{0} θ0不参与正则化。