利用keras搭建神经网络拟合非线性函数
神经网络有着一个非常奇妙的结构,它的数学原理虽然相对简单,但是能做的事情却不少,数学家已经证明,具有2层(输入层除外)和非线性激活函数的神经网络,只要在这些层中有足够多的神经元,就可以近似任何函数(严格的说法是,激活函数使用了非线性sigmoid函数的感知机).
那么,如果只有两层就够了,为什么人们现在还在使用更深层次的网络呢? 仅仅因为虽然这两层网络“能够”学习任何东西,这并不意味着它们很容易优化。在实践中,如果网络的产能过剩,他们就有能力提供足够好的解决方案,即使网络本身没有尽可能地优化。
本片文章就是针对这个规则的实践和验证,我们用两层网络,去近似模拟各种非线性函数,事不宜迟,我们开始。
正弦函数
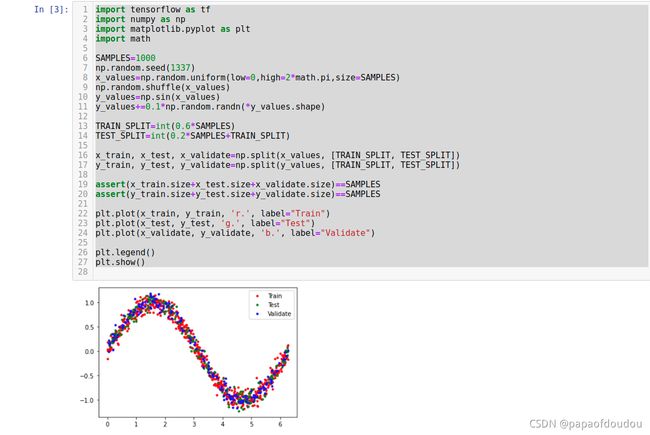
首先生成正弦函数的样本数据
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import math
SAMPLES=1000
np.random.seed(1337)
x_values=np.random.uniform(low=0,high=2*math.pi,size=SAMPLES)
np.random.shuffle(x_values)
y_values=np.sin(x_values)
y_values+=0.1*np.random.randn(*y_values.shape)
TRAIN_SPLIT=int(0.6*SAMPLES)
TEST_SPLIT=int(0.2*SAMPLES+TRAIN_SPLIT)
x_train, x_test, x_validate=np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT])
y_train, y_test, y_validate=np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT])
assert(x_train.size+x_test.size+x_validate.size)==SAMPLES
assert(y_train.size+y_test.size+y_validate.size)==SAMPLES
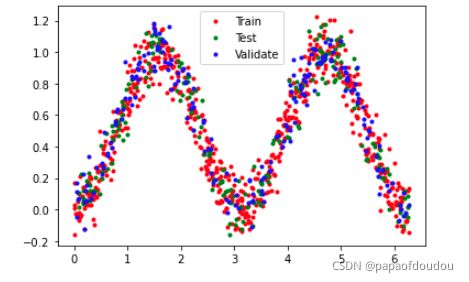
plt.plot(x_train, y_train, 'r.', label="Train")
plt.plot(x_test, y_test, 'g.', label="Test")
plt.plot(x_validate, y_validate, 'b.', label="Validate")
plt.legend()
plt.show()
运行结果,查看样本数据:
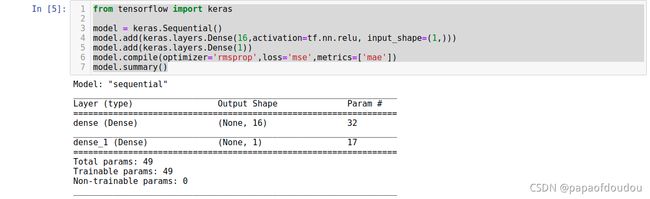
定义模型结构
from tensorflow import keras
model = keras.Sequential()
model.add(keras.layers.Dense(16,activation=tf.nn.relu, input_shape=(1,)))
model.add(keras.layers.Dense(1))
model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])
model.summary()模型摘要信息:
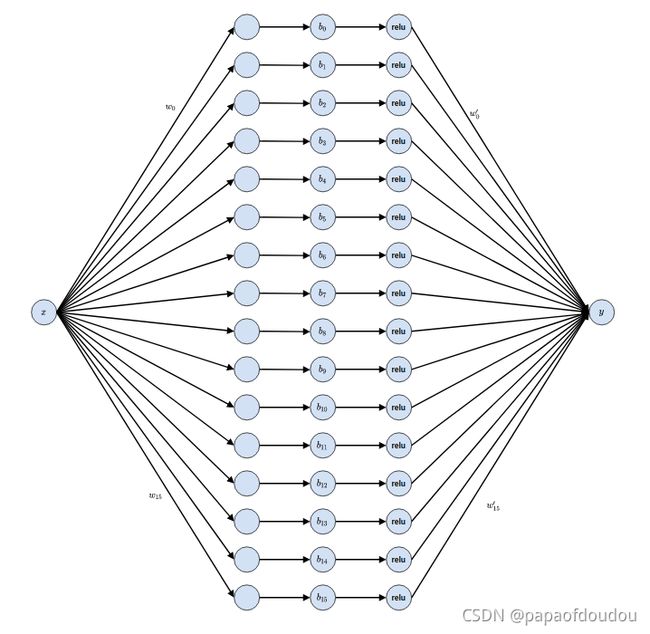
其中输入层有 16 个神经元,共 2 层连接,所以全部的连接数为 16x2=32,每一个神经元都有一个 bias,网络总共有 17 个 bias。输入的 16,以及输出的 1。所以总的参数为 32+17=49,它的俄网络模型是这个样子的:
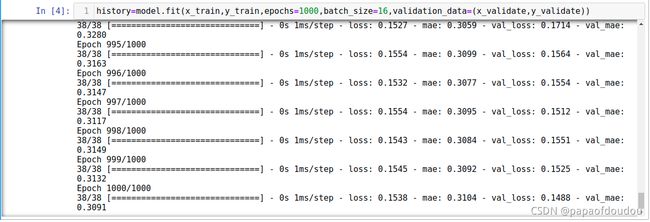
训练模型:
history=model.fit(x_train,y_train,epochs=1000,batch_size=16,validation_data=(x_validate,y_validate))
利用 keras 的 fit() 方法能够很好的训练。下面就一些参数做一下最基本的解释:
x_train, y_train 表示最基本的训练数据。
epochs 训练的周期,一般来说,周期越长,训练越精确,但是,一般来说,训练的时间到一定阶段,训练精度不会有很大差别。在这种清况下,一般要考虑去优化模型了。
batch_size 用于往网络中一次送入多少数据,如果值为 1,我们每一次会更新 weight 和 bias,并且会估计网络预测的损失,为下一次的运行做更精确的估计。越小的值,会带来很大的计算量,占用更多的计算资源。如果我们把值定要 600,一次性可以计算出更多的数据,但是会降低模型的精度。所以最好的方式是把值设置为 16 或者是 32。这个值的选择,实际上精度与时间花费权衡的结果。
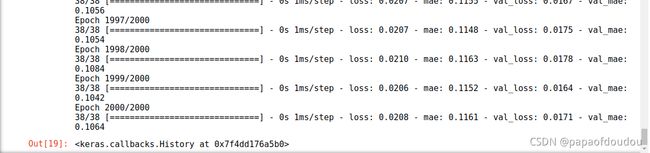
我们分析一下训练过程的收敛情况:
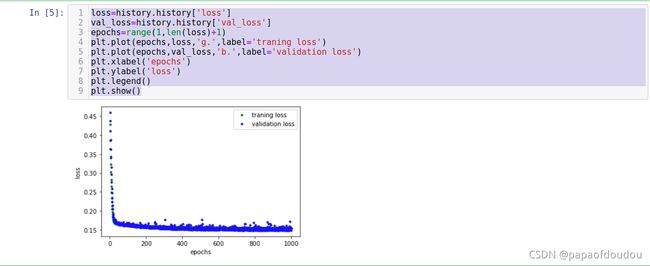
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=range(1,len(loss)+1)
plt.plot(epochs,loss,'g.',label='traning loss')
plt.plot(epochs,val_loss,'b.',label='validation loss')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend()
plt.show()根据compile参数metrics,history包含不同的内容。比如,当某一次metrics=['accuracy']时,history字典类型,包含val_loss,val_acc,loss,acc四个key值。
该图显示了每个时期的损失(或模型的预测与实际数据之间的差异)。有几种计算损失的方法,我们使用的方法是均方误差。对于训练和验证数据有明显的损失值。
我们可以看到,损失的数量在前面迅速减少,然后趋于平稳。这意味着该模型正在改进并产生更准确的预测!
我们的目标是在模型不再改善或训练损失小于验证损失 (Validation Loss) 时停止训练,这意味着该模型已经学会了很好地预测训练数据,也不需要新的数据来提高精度。
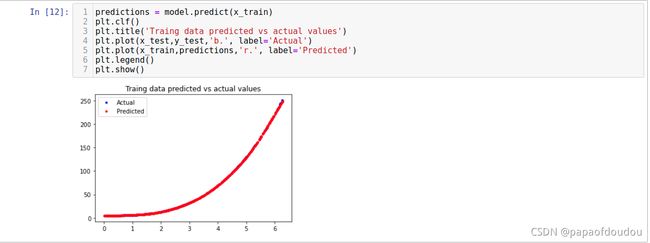
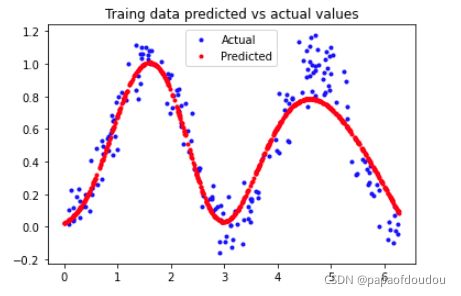
我们最关心的,当然是训练的结果了,图形化表示:
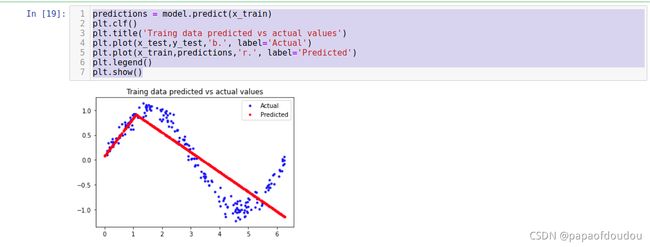
predictions = model.predict(x_train)
plt.clf()
plt.title('Traing data predicted vs actual values')
plt.plot(x_test,y_test,'b.', label='Actual')
plt.plot(x_train,predictions,'r.', label='Predicted')
plt.legend()
plt.show()二次函数:
将sin函数换为二次函数
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import math
SAMPLES=1000
np.random.seed(1337)
x_values=np.random.uniform(low=0,high=2*math.pi,size=SAMPLES)
np.random.shuffle(x_values)
#y_values=np.sin(x_values)
y_values=x_values*x_values
y_values+=0.1*np.random.randn(*y_values.shape)
TRAIN_SPLIT=int(0.6*SAMPLES)
TEST_SPLIT=int(0.2*SAMPLES+TRAIN_SPLIT)
x_train, x_test, x_validate=np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT])
y_train, y_test, y_validate=np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT])
assert(x_train.size+x_test.size+x_validate.size)==SAMPLES
assert(y_train.size+y_test.size+y_validate.size)==SAMPLES
plt.plot(x_train, y_train, 'r.', label="Train")
plt.plot(x_test, y_test, 'g.', label="Test")
plt.plot(x_validate, y_validate, 'b.', label="Validate")
plt.legend()
plt.show()
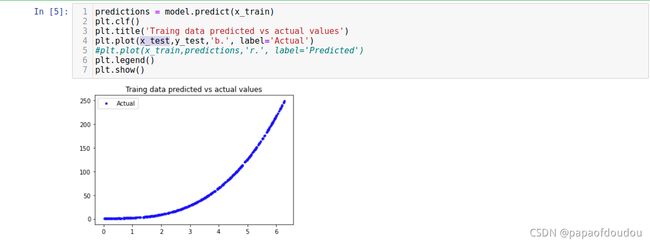
训练效果要比正弦好很多,训练代码不变:
验证推理:
三次函数
代码段:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import math
SAMPLES=2000
np.random.seed(1337)
x_values=np.random.uniform(low=0,high=2*math.pi,size=SAMPLES)
np.random.shuffle(x_values)
#y_values=np.sin(x_values)
y_values=x_values*x_values*x_values + 1
y_values+=0.1*np.random.randn(*y_values.shape)
TRAIN_SPLIT=int(0.6*SAMPLES)
TEST_SPLIT=int(0.2*SAMPLES+TRAIN_SPLIT)
x_train, x_test, x_validate=np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT])
y_train, y_test, y_validate=np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT])
assert(x_train.size+x_test.size+x_validate.size)==SAMPLES
assert(y_train.size+y_test.size+y_validate.size)==SAMPLES
plt.plot(x_train, y_train, 'r.', label="Train")
plt.plot(x_test, y_test, 'g.', label="Test")
plt.plot(x_validate, y_validate, 'b.', label="Validate")
plt.legend()
plt.show()
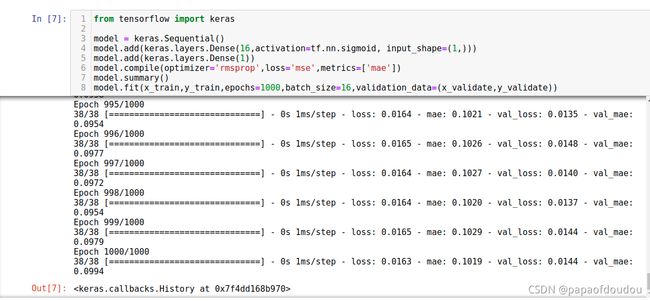
用sigmoid激活函数替代relu
我们把原来用的relu激活函数换乘sigmoid函数看会不会改善,仅仅修改修改一行即可实现
from tensorflow import keras
model = keras.Sequential()
model.add(keras.layers.Dense(16,activation=tf.nn.sigmoid, input_shape=(1,)))
model.add(keras.layers.Dense(1))
model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])
model.summary()
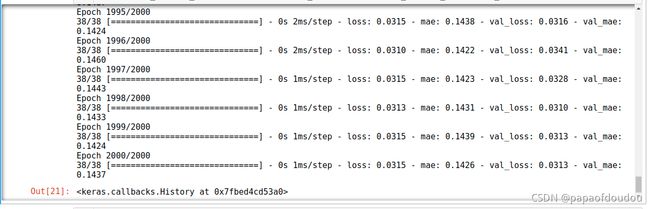
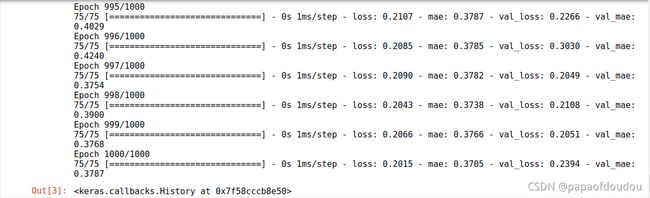
model.fit(x_train,y_train,epochs=1000,batch_size=16,validation_data=(x_validate,y_validate))训练结果如下,如果只看训练结果,使用sigmoid训练出来的结果要好很多。
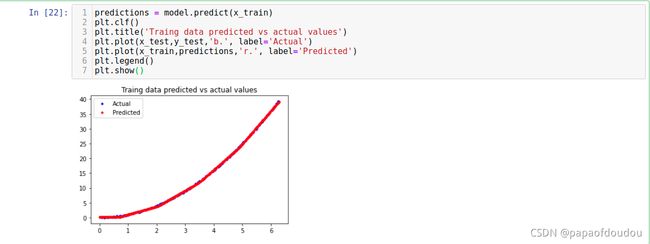
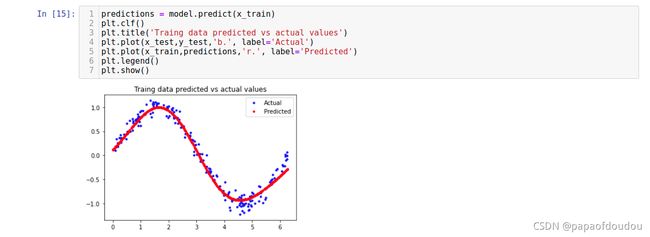
看一下实际的推理波形:
根据训练的数据推理得到输出图形可以看出,使用sigmoid后确实好很多。
对三次函数的拟合,sigmoid也要明显优于relu激活函数。
稍微复杂一些的函数拟合
y_values=np.sin(x_values)**2训练:
拟合效果:
还是非常不错。
总结:
上面我们用搭建的简易神经网络拟合了三种非线性函数,分别是正弦函数,二次函数和三次函数,发现效果都还不错,测试数据很好的拟合了函数的形状。
很有意思的一点是,对于不同的函数拟合过程,在程序中,我们只变换了函数的数值解析式,而并没有改变网络的结构,也就是说,我们用了同一个网络结构,仅仅重新训练改变训练参数,就可以拟合完全不一样的函数图形,相当于网络吃什么数据,给什么样模态的结果。这个特点给算法的应用部署带来了方便,因为我们不需要频繁更换网络结构。
算法的上限是由网络结构定义的,下限则是数据训练决定的,这有点像我们人类,我们生来带一个不可编辑的大脑,必须承认每个人的天分是有差异的,就好比算法和网络本身是有优劣的,后天的充足数据训练(相当于我们上学读书的学习阶段),虽然无法突破天分的天花板,但可以最大限度的发挥我们在天分框架下的能力。但如果你不好好接受训练(少壮不努力),那么本来你可以做好的事情,可能也做不好了(老大徒伤悲).