神经网络与深度学习：回归问题

---

1.机器学习基础

机器学习：从数据中学习。
1.建立模型
2.学习模型
3.预测房价
学习算法：从数据中产生模型的算法。

1.1监督学习

Supervised Learning

1.2无监督学习

Unsupervised Learning
在样本数据没有标记的情况下，挖掘出数据内部蕴含的关系。
聚类：把相似度高的样本聚合在一起。

1.3半监督学习

Semi-Supervised Learning
将有监督学习和无监督学习相结合，综合使用大量的没有标记数据和少量有标记的数据共同进行学习。

---

2.一元线性回归

模型：y=wx+b
模型变量：x
模型参数：w：权重(weights)；b：偏置值(bias)

最佳拟合直线应该使得所有点的残差累计值最小。

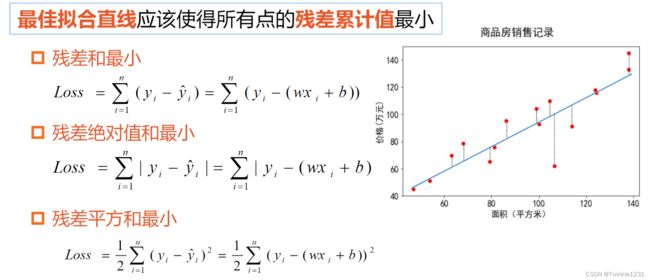
损失函数：估量模型的预测值与真实值的不一致程度
最小二乘法：基于均方误差最小化来进行模型求解的方法

---

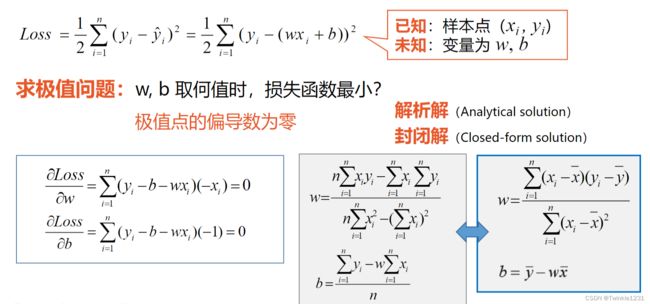
3.解析法实现一元回归

3.1 Python实现

#load dataset
x=[137.97,104.5,100.00,124.32,79.20,99.00,124.00,114.00,
106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21]
y=[145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,
62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.3]
 
#Calculate w, b
meanX=sum(x)/len(x)    
meanY=sum(y)/len(y)    
 
sumXY=0.0              
sumX=0.0               
#Calculate in cycle
for i in range(len(x)):            
    sumXY+=(x[i]-meanX)*(y[i]-meanY)
    sumX+=(x[i]-meanX)*(x[i]-meanX)
#Calculate w,b
w=sumXY/sumX
b=meanY-w*meanX
#Output
print('w=',w)
print('b=',b)

3.2 NumPy实现

from numpy.core.fromnumeric import mean
#load dataset
x=np.array([137.97,104.5,100.00,124.32,79.20,99.00,124.00,114.00,
106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
y=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,
62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.3])
#Calculate w,b
meanX=np.mean(x)
meanY=np.mean(y)
sumXY=np.sum((x-meanX)*(y-meanY))
sumX=np.sum((x-meanX)*(x-meanX))
 
w=sumXY/sumX
b=meanY-w*meanX
print('w=',w)
print('b=',b)

3.3 TensorFlow实现

import tensorflow as tf
#load dataset
x=tf.constant([137.97,104.5,100.00,124.32,79.20,99.00,124.00,114.00,
106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
y=tf.constant([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,
62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.3])
#Calculate w,b
meanX=tf.reduce_mean(x)
meanY=tf.reduce_mean(y)
sumXY=tf.reduce_sum((x-meanX)*(y-meanY))
sumX=tf.reduce_sum((x-meanX)*(x-meanX))
 
w=sumXY/sumX
b=meanY-w*meanX
print('w=',w)
print('b=',b)

---

4.多元线性回归

多元回归：回归分析中包括两个或两个以上的自变量。
多元线性回归：因变量和自变量之间是线性关系。