遗传算法优化神经网络—MATLAB实现

一、算法介绍

1.1 遗传算法

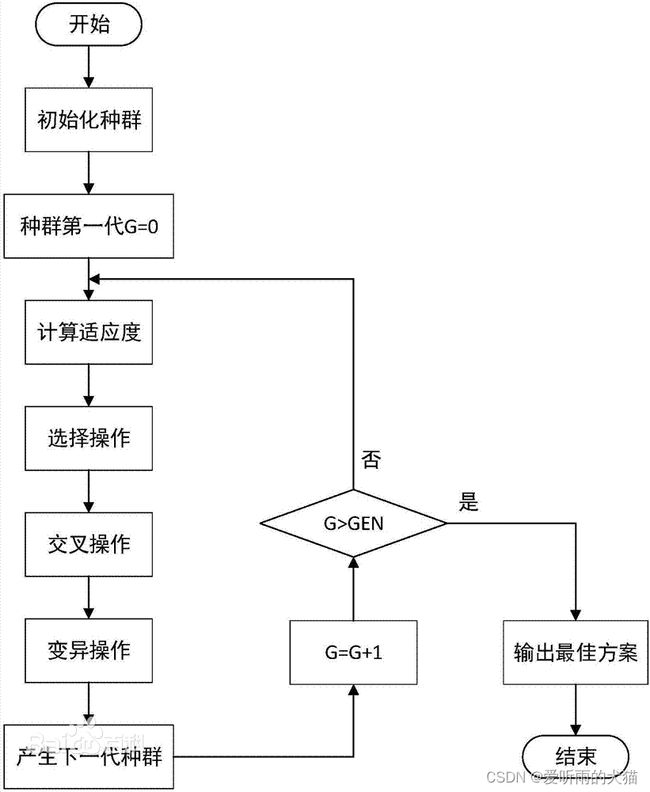
  遗传算法（Genetic Algorithm，GA）最早是由美国的 John holland于20世纪70年代提出，该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式，利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时，相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
  具体介绍请看这篇遗传算法详细介绍以及基于遗传算法和非线性规划函数的寻优算法—MATLAB实现
  算法流程如下：

1.2BP神经网络

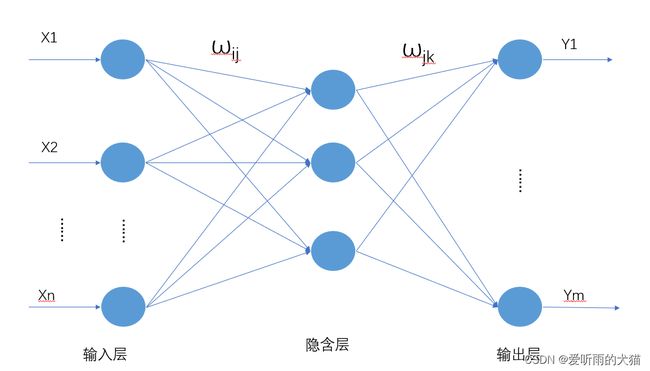
  BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一。
  人工神经网络无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果。作为一种智能信息处理系统，人工神经网络实现其功能的核心是算法。BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。
  基本BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。误差反传是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。
  具体介绍请看这篇BP神经网络分类以及对算法进行改进—MATLAB实现
  BP神经网络结构：

二、MATLAB实现

2.1 问题介绍

  有一组广告销售额的数据为200$\times$ 4的矩阵，前3列为输入变量，最后一列为销售额，输出变量，共200个数据。将数据的前150组训练模型，后50组来验证模型准确率。
  数据大致如下：

TV	radio	newspaper	sales
230.1	37.8	69.2	22.1
44.5	39.3	45.1	10.4
17.2	45.9	69.3	9.3
···	···	···	···

2.2 未优化的BP神经网络

clc;clear all;close all;
%读取数据
data=xlsread('广告和销售额数据.xlsx');
%训练预测数据
data_train=data(1:150,1:4);
data_test=data(151:200,1:4);

input_train=data_train(:,1:3)';
output_train=data_train(:,4)';

input_test=data_test(:,1:3)';
output_test=data_test(:,4)';

%数据归一化
[inputn,mininput,maxinput,outputn,minoutput,maxoutput]=premnmx(input_train,output_train); %对p和t进行字标准化预处理 
net=newff(minmax(inputn),[10,1],{'tansig','purelin'},'trainlm');

net.trainParam.epochs=1000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.001;
net.trainParam.show=200;

%网络训练
net=train(net,inputn,outputn);
%数据归一化
inputn_test = tramnmx(input_test,mininput,maxinput);
an=sim(net,inputn_test);
test_simu=postmnmx(an,minoutput,maxoutput);
error=test_simu-output_test;
e=sum(abs(test_simu-output_test))

Yn=test_simu;            
figure(1)                        %绘图
plot(Yn,'r*-')                %绘制预测值曲线
hold on                       %继续绘图
plot(output_test,'bo')                  %实际值曲线
legend('预测值','实际值')      %图例

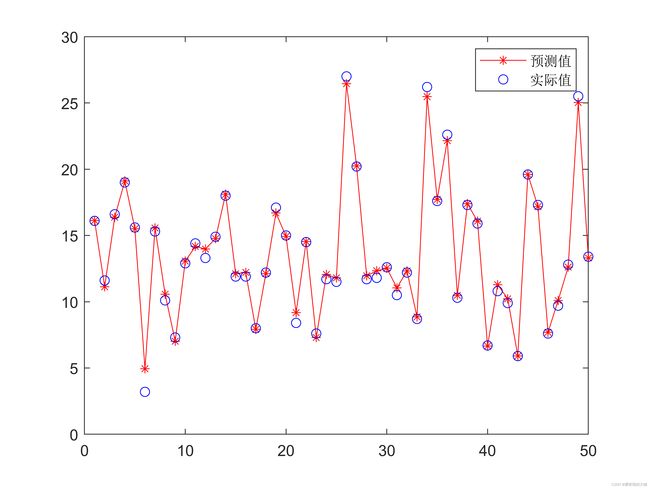
预测结果于真实值对比图如下：

重复5次求得每次的结果误差为：

	结果误差
第一次	15.8820
第二次	15.0166
第三次	17.7604
第四次	18.8338
第五次	17.9484

2.3 遗传算法优化的的BP神经网络

2.3.1 适应度函数

适应度函数用训练数据训练BP神经网络,并且把训练数据预测误差作为个体适应度值。

function error = fun(x,inputnum,hiddennum,outputnum,~,inputn,outputn)
%该函数用来计算适应度值,BP神经网络预测，记录预测误差
%运用新版本netff
%x          input     个体
%inputnum   input     输入层节点数
%outputnum  input     隐含层节点数
%net        input     网络
%inputn     input     训练输入数据
%outputn    input     训练输出数据

%error      output    个体适应度值
%提取
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);

net=newff(inputn,outputn,hiddennum);
%网络进化参数
net.trainParam.epochs=1000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.001;
net.trainParam.show=100;
net.trainParam.showWindow=0;
 
%网络权值赋值
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);

%网络训练
net=train(net,inputn,outputn);

an=sim(net,inputn);

error=sum(abs(an-outputn));

2.3.2 选择操作

选择操作采用轮盘赌法从种群中选择适应度好的个体组成新种群。

function ret=Select(individuals,sizepop)
% 该函数用于进行选择操作
% individuals input    种群信息
% sizepop     input    种群规模
% ret         output   选择后的新种群

%求适应度值倒数   
fitness1=10./individuals.fitness; %individuals.fitness为个体适应度值

%个体选择概率
sumfitness=sum(fitness1);
sumf=fitness1./sumfitness;

%采用轮盘赌法选择新个体
index=[]; 
for i=1:sizepop   %sizepop为种群数
    pick=rand;
    while pick==0    
        pick=rand;        
    end
    for i=1:sizepop    
        pick=pick-sumf(i);        
        if pick<0        
            index=[index i];            
            break;  
        end
    end
end


%新种群
individuals.chrom=individuals.chrom(index,:);   %individuals.chrom为种群中个体
individuals.fitness=individuals.fitness(index);
ret=individuals;

2.3.3 交叉操作

交叉操作从种群中选择两个个体,按一定概率交叉得到新个体。

function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
%本函数完成交叉操作
% pcorss                input  : 交叉概率
% lenchrom              input  : 染色体的长度
% chrom     input  : 染色体群
% sizepop               input  : 种群规模
% ret                   output : 交叉后的染色体

 for i=1:sizepop  %每一轮for循环中，可能会进行一次交叉操作，染色体是随机选择的，交叉位置也是随机选择的，%但该轮for循环中是否进行交叉操作则由交叉概率决定（continue控制）
     % 随机选择两个染色体进行交叉
     pick=rand(1,2);
     while prod(pick)==0
         pick=rand(1,2);
     end
     index=ceil(pick.*sizepop);
     % 交叉概率决定是否进行交叉
     pick=rand;
     while pick==0
         pick=rand;
     end
     if pick>pcross
         continue;
     end
     flag=0;
     while flag==0
         % 随机选择交叉位
         pick=rand;
         while pick==0
             pick=rand;
         end
         pos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置，即选择第几个变量进行交叉，注意：两个染色体交叉的位置相同
         pick=rand; %交叉开始
         v1=chrom(index(1),pos);
         v2=chrom(index(2),pos);
         chrom(index(1),pos)=pick*v2+(1-pick)*v1;
         chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
         flag1=test(lenchrom,bound,chrom(index(1),:));  %检验染色体1的可行性
         flag2=test(lenchrom,bound,chrom(index(2),:));  %检验染色体2的可行性
         if   flag1*flag2==0
             flag=0;
         else flag=1;
         end    %如果两个染色体不是都可行，则重新交叉
     end
 end
ret=chrom;

2.3.3 变异操作

变异操作从种群中随机选择一个个体,按一定概率变异得到新个体。

function ret=Mutation(pmutation,lenchrom,chrom,sizepop,num,maxgen,bound)
% 本函数完成变异操作
% pcorss                input  : 变异概率
% lenchrom              input  : 染色体长度
% chrom     input  : 染色体群
% sizepop               input  : 种群规模
% opts                  input  : 变异方法的选择
% pop                   input  : 当前种群的进化代数和最大的进化代数信息
% bound                 input  : 每个个体的上届和下届
% maxgen                input  ：最大迭代次数
% num                   input  : 当前迭代次数
% ret                   output : 变异后的染色体
for i=1:sizepop   %每一轮for循环中，可能会进行一次变异操作，染色体是随机选择的，变异位置也是随机选择的，
    %但该轮for循环中是否进行变异操作则由变异概率决定（continue控制）
    % 随机选择一个染色体进行变异
    pick=rand;
    while pick==0
        pick=rand;
    end
    index=ceil(pick*sizepop);
    % 变异概率决定该轮循环是否进行变异
    pick=rand;
    if pick>pmutation
        continue;
    end
    flag=0;
    while flag==0
        % 变异位置
        pick=rand;
        while pick==0      
            pick=rand;
        end
        pos=ceil(pick*sum(lenchrom));  %随机选择了染色体变异的位置，即选择了第pos个变量进行变异
    
        pick=rand; %变异开始     
        fg=(rand*(1-num/maxgen))^2;
        if pick>0.5
            chrom(i,pos)=chrom(i,pos)+(bound(pos,2)-chrom(i,pos))*fg;
        else
            chrom(i,pos)=chrom(i,pos)-(chrom(i,pos)-bound(pos,1))*fg;
        end   %变异结束
        flag=test(lenchrom,bound,chrom(i,:));     %检验染色体的可行性
    end
end
ret=chrom;

2.3.4 主函数

% 清空环境变量
clc
clear
close all;
% 
%% 网络结构建立
%读取数据
data=xlsread('广告和销售额数据.xlsx');
%节点个数
inputnum=3;  %输入变量的个数
hiddennum=10;
outputnum=1;  %输出变量的个数
data_train=data(1:150,1:4);
data_test=data(151:200,1:4);

input_train=data_train(:,1:3)';
output_train=data_train(:,4)';

input_test=data_test(:,1:3)';
output_test=data_test(:,4)';

[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
net=newff(inputn,outputn,hiddennum,{'tansig','purelin'},'trainlm');

%% 遗传算法参数初始化
maxgen=50;                         %进化代数，即迭代次数
sizepop=20;                        %种群规模
pcross=[0.3];                       %交叉概率选择，0和1之间
pmutation=[0.1];                    %变异概率选择，0和1之间

%节点总数
numsum=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum;

lenchrom=ones(1,numsum);        
bound=[-3*ones(numsum,1) 3*ones(numsum,1)];    %数据范围

%------------------------------------------------------种群初始化--------------------------------------------------------
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %将种群信息定义为一个结构体
avgfitness=[];                      %每一代种群的平均适应度
bestfitness=[];                     %每一代种群的最佳适应度
bestchrom=[];                       %适应度最好的染色体
%初始化种群
for i=1:sizepop
    %随机产生一个种群
    individuals.chrom(i,:)=Code(lenchrom,bound);    %编码（binary和grey的编码结果为一个实数，float的编码结果为一个实数向量）
    x=individuals.chrom(i,:);
    %计算适应度
    individuals.fitness(i)=fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn);   %染色体的适应度
end

%找最好的染色体
[bestfitness, bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:);  %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[avgfitness bestfitness]; 
 
%% 迭代求解最佳初始阀值和权值
% 进化开始
for i=1:maxgen
    
    % 选择
    individuals=Select(individuals,sizepop); 
    avgfitness=sum(individuals.fitness)/sizepop;
    %交叉
    individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
    % 变异
    individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);
    
    % 计算适应度 
    for j=1:sizepop
        x=individuals.chrom(j,:); %解码
        individuals.fitness(j)=fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn);   
    end
    
  %找到最小和最大适应度的染色体及它们在种群中的位置
    [newbestfitness,newbestindex]=min(individuals.fitness);
    [worestfitness,worestindex]=max(individuals.fitness);
    % 代替上一次进化中最好的染色体
    if bestfitness>newbestfitness
        bestfitness=newbestfitness;
        bestchrom=individuals.chrom(newbestindex,:);
    end
    individuals.chrom(worestindex,:)=bestchrom;
    individuals.fitness(worestindex)=bestfitness;
    
    avgfitness=sum(individuals.fitness)/sizepop;
    
    trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度

end
%% 遗传算法结果分析 
 figure(1)
[r, c]=size(trace);

plot([1:r]',trace(:,1),'b--');%平均适应度曲线
hold on                       %继续绘图
plot([1:r]',trace(:,2),'r-'); %每一代种群的最佳适应度曲线             
title(['适应度曲线  ' '终止代数＝' num2str(maxgen)]);
xlabel('进化代数');ylabel('适应度');
legend('平均适应度','最佳适应度');
x=bestchrom;

%% 把最优初始阀值权值赋予网络预测
% %用遗传算法优化的BP网络进行值预测
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);

net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=reshape(B2,outputnum,1);


%% BP网络训练
%网络进化参数
net.trainParam.epochs=1000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.001;

%网络训练
[net,per2]=train(net,inputn,outputn);

%% BP网络预测
%数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
an=sim(net,inputn_test);
test_simu=mapminmax('reverse',an,outputps);
error=test_simu-output_test;
e=sum(abs(test_simu-output_test))


Yn=test_simu;        
figure(2)                        %绘图
plot(Yn,'r*-')                %绘制预测值曲线clc

hold on                       %继续绘图
plot(output_test,'bo')                  %实际值曲线
legend('预测值','实际值')      %图例

预测结果于真实值对比图如下：

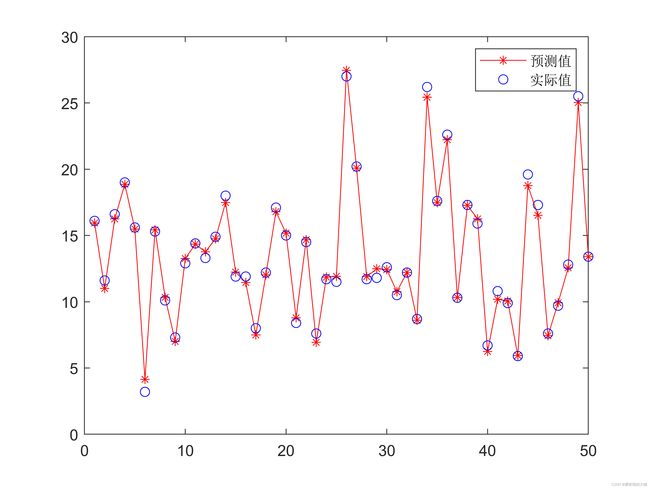
重复5次求得每次的结果误差为：

	结果误差
第一次	14.1473
第二次	26.4658
第三次	15.5426
第四次	14.3759
第五次	18.8988

将这个结果与之前的未优化的结果进行对比可以看出，的确有更好的结果出现了，起到了优化的作用。但同时也会有部分的较差的结果，这是因为遗传算法陷于了局部最优的情况。我们可以用其他算法例如粒子群算法或者模拟退火算法对此进一步优化。

代码链接：https://pan.baidu.com/s/1hOqbNXAUapEL609qwZpiIA
提取码：6666