Dijkstra算法原理与实现
目录
前言
一、用途
二、原理与实现
1.流程
2.伪代码
3.代码
三、参考文献
前言
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
其原理这个动态图可以做出解释:
一、用途
Dijkstra算法:用来解决单源最短路问题。给定图G和起点s,通过算法得到S到达其他每个顶点的最短距离。
限制条件:图G中不存在负权值的边。
二、原理与实现
1.流程
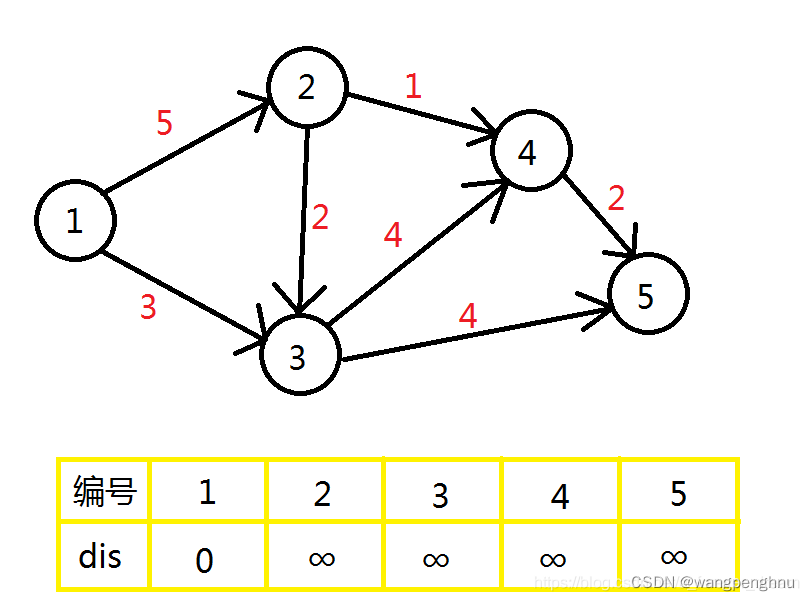
步骤1.1,比如说现在有这样一张 5 个点的图(起点是 1):
下面的 d i s 数组表示现在每个点到起点的距离,因为其他点一开始都不知道,所以我们需要初始化成一个比较大的数。
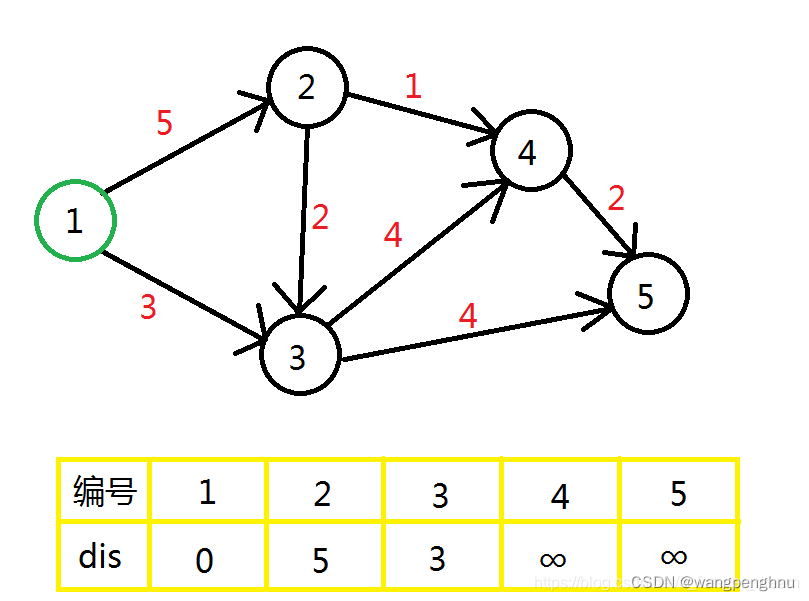
那么一开始离起点最近的肯定就是起点自己啦,于是用点 1进行一次更新,点 2 , 3 会被更新。
步骤1.2
为了方便,我们将1号点标成绿色,表示这个点已经用过了。
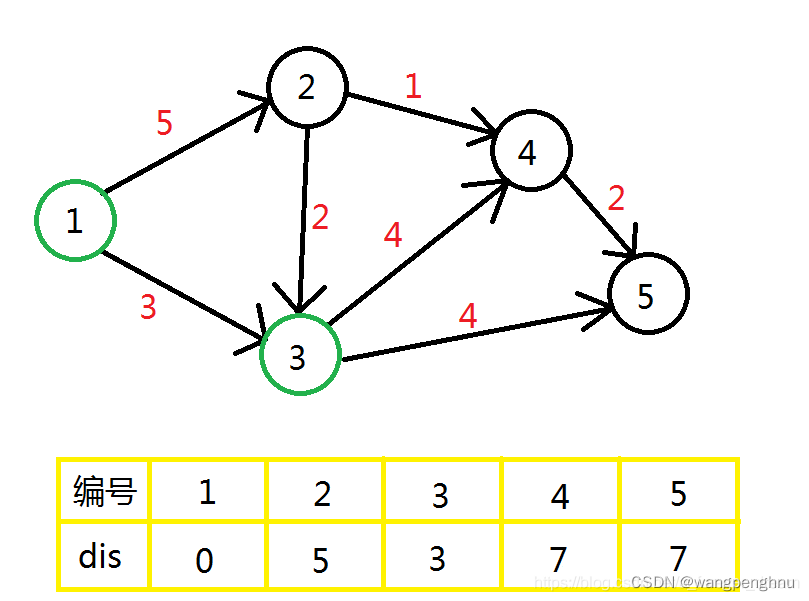
那么现在能用的点有: 2 , 3 , 4 , 5,其中离起点最近的是点 3。然后用点 3进行一次更新,点 4 , 5会被更新。
步骤1.3
现在能用的有: 2 , 4 , 5,离起点最近的是点 2。
用点2 进行一次更新,点 4 会被更新,而点 3 并不会,因为 d i s [ 3 ] < d i s [ 2 ] + 2 。
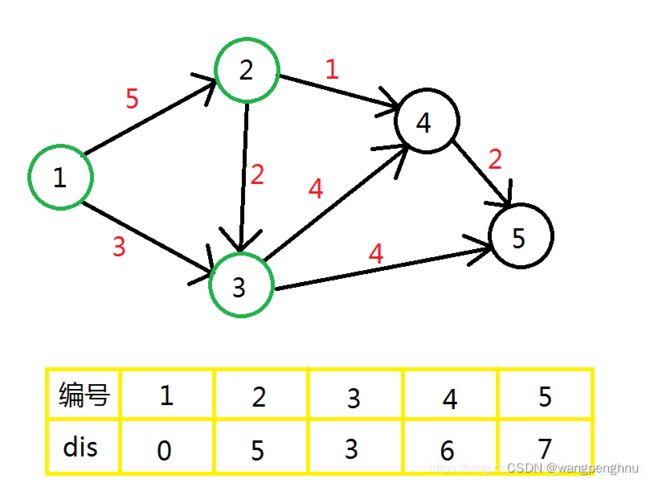
步骤1.4
现在能用的有: 4 , 5,离起点最近的是点 4。
用点 4 进行一次更新,没有点会被更新。
最后用点 5也更新不了其他点,于是我们就这样求出了起点到每个点的最短路。
2.伪代码
Dijkstra(G, d[], s)
{
初始化;
for(循环n次)
{
u = 使d[u]最小的还未被访问的顶点的标号;
记u已被访问;
for(从u出发能到达的所有顶点v)
{
if(v未被访问 && 以u为中介点使s到顶点v的最短距离d[v]更优)
{
优化d[v];
}
}
}
}3.代码
主循环
void Dijkstra(const int x, const int y)
{
openlist.clear();
closelist.clear();
openlist.push_back(x);
plan_ways_map[x]->G = 0;
plan_ways_map[x]->H = 0;
plan_ways_map[x]->F = Calculatef(x);
while(!openlist.empty())
{
int minidnode = Findleastf(openlist);
openlist.remove(minidnode);
closelist.push_back(minidnode);
std::vector candiates = Getnextnode(minidnode);
for(int i = 0; i < candiates.size(); ++i)
{
if(!Isinlist(candiates[i], openlist))
{
plan_ways_map[candiates[i]]->parent = minidnode;
plan_ways_map[candiates[i]]->G = Calculateg(x, candiates[i]);
plan_ways_map[candiates[i]]->H = 0;
plan_ways_map[candiates[i]]->F = Calculatef(candiates[i]);
openlist.push_back(candiates[i]);
}else{
double tempg = Calculateg(x, candiates[i]);
if(tempg > plan_ways_map[candiates[i]]->G)
{
continue;
}else{
plan_ways_map[candiates[i]]->parent = minidnode;
plan_ways_map[candiates[i]]->G = tempg;
plan_ways_map[candiates[i]]->F = Calculatef(candiates[i]);
}
}
if(Isinlist(y, openlist))
{
plan_ways_map[y]->parent = minidnode;
std::cout << "---------------------------------------------------" << std::endl;
std::cout << "find!" << std::endl;
int i = y;
while(i != -1)
{
plan_path.push_back(i);
i = plan_ways_map[i]->parent;
}
std::reverse(plan_path.begin(), plan_path.end());
isfindpath = true;
return;
}
}
}
std::cout << "---------------------------------------------------" << std::endl;
std::cout << "not find" << std::endl;
return;
} 其他函数
//计算起点到当前点的代价
double Calculateg(const int x, const int idg) const
{
}
//计算总代价,预置A*接口,Dijkstra相当于简化版A*
double Calculatef(const int idf) const
{
}
//从list中找出总代价的点
int Findleastf(const std::list &listx) const
{
}
//从当前索引idx找到可行的下一点集合
std::vector Getnextnode(const int idx) const
{
}
//判断x点是否在list中
bool Isinlist(const int x, const std::list &listx) const
{
} 三、参考文献
1.迪杰斯特拉算法详解_Hypoc_的博客-CSDN博客_迪杰斯特拉算法
2.C++ 求最短路径问题之Dijkstra算法(一)_YF_Li123的博客-CSDN博客_c++最短路径算法